目录
1 三角函数与圆,角度和弧度
1.1 三角形
1.2 圆形
2 角度
3 弧度 rad
4 角度,弧度的换算
2 三角函数
1 三角函数与圆,角度和弧度
1.1 三角形
- 角度
- 弧长
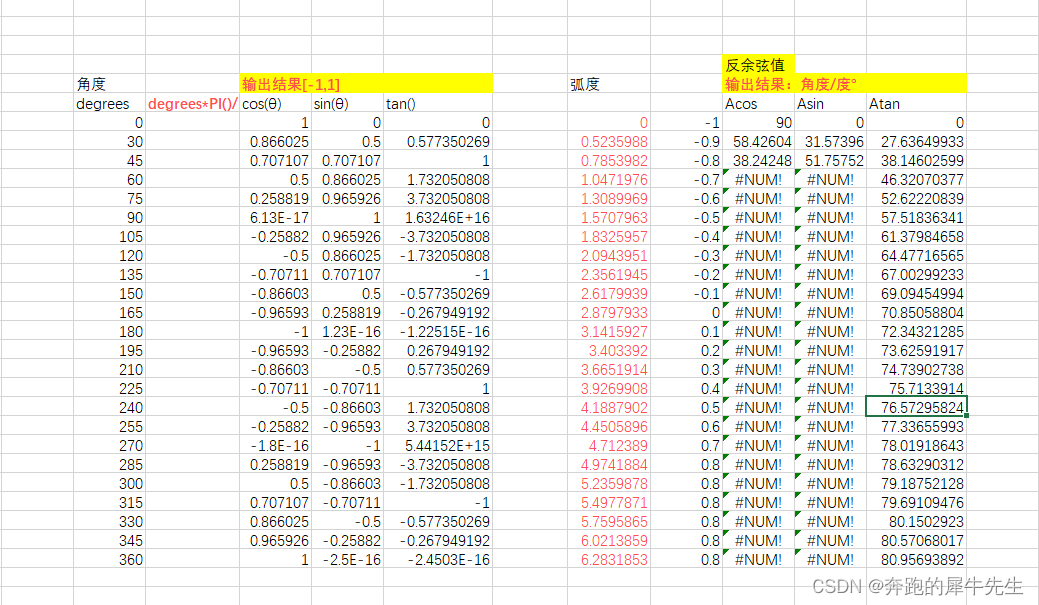
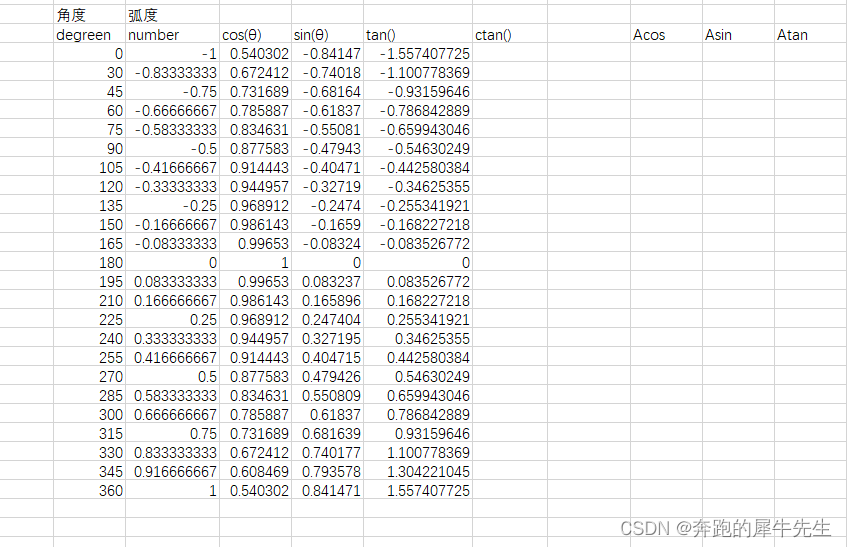
- sin()
- cos()
- tan()
1.2 圆形
- 半径,周长,弧长
- 半径
- 面积
2 角度
- 角度取值范围 [0,360]
- [angle(角度)]∶两条相交直线中的任何一条与另一条相叠合时必须转动的量的量度,转动在这两条直线的所在平面上并绕交点进行。
3 弧度 rad
- 弧度不受限制圆形--可以很大,不只圆形的2Π
- 弧度,在数学和物理中,弧度是角的度量单位。缩写是rad。
- 定义:弧长等于半径的弧,其所对的圆心角为1弧度。
- (即两条射线从圆心向圆周射出,形成一个夹角和夹角正对的一段弧。当这段弧长正好等于圆的半径时,两条射线的夹角的弧度为1)。
- 所以说,弧度是指在一个圆中,弧长除以半径的值,即|弧度|=弧长÷半径。
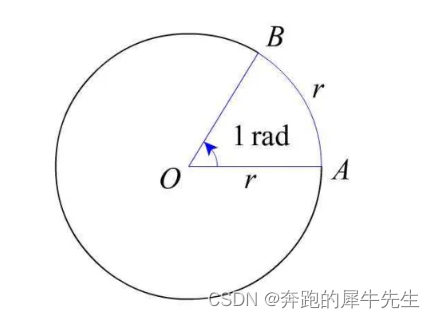

4 角度,弧度的换算
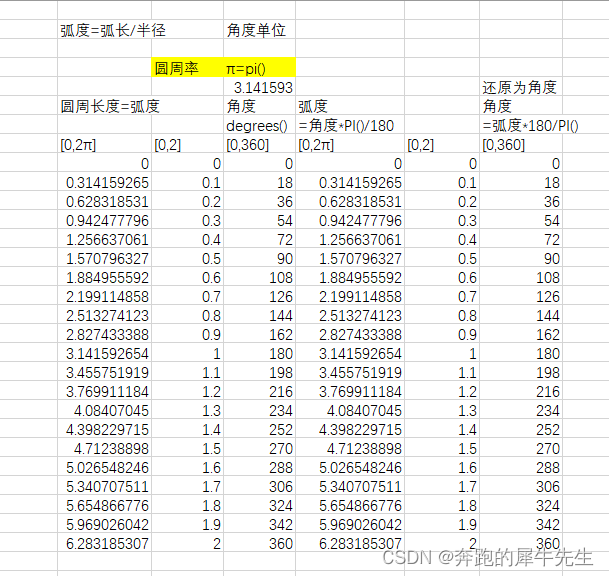
- 角度和弧度互相换算
- 弧度=角度*PI()/180
- 角度=弧度*180/PI()
1弧度=57.29578度
根据弧度的定义,以长为圆周长(2πr)的弧所对的圆心角为2π 弧度,半个圆周长的弧所对的圆心角为π 弧度。
于是,角度与弧度间换算关系就十分明了了。因为360度=2π,所以,1度=π/180≈0.01745弧度,1弧度=180/π=57.29578度。
弧度制与角度制的换算公式:1度=π/180≈0.01745弧度,1弧度=180/π≈57.3度。角的度量单位通常有两种,一种是角度制,另一种就是弧度制。
1弧度=180/pai 度
1度=pai/180 弧度
记不住的时候就像圆
一个圆是360度,2pai弧度
2 三角函数
3 三角函数的定义