数学中矩的概念来自物理学。在物理学中，矩是表示距离和物理量乘积的物理量，表征物体的空间分布。矩在统计学和图像中都有很重要作用，我们常用的Adam优化器其全称为自适应矩估计优化器。本文将介绍各阶矩的理解和不同场景的应用。

Key Words：矩的意义、统计矩、图像矩

1、矩的物理意义

在物理学中，矩是表示距离和物理量乘积的物理量，表征物体的空间分布。矩通常需要一个参考点（基点或参考系）来定义距离。如力和参考点距离乘积得到的力矩（或扭矩），原则上任何物理量和距离相乘都会产生矩，如：质量，电荷分布等。

如果点表示质量：

• 零阶矩：表示总质量。
• 一阶原点矩：表示质心。
• 二阶原点矩：表示转动惯量。

如果点表示高度：

• 零阶矩：表示所有点高度之和。
• 一阶原点矩：表示点的位置和对应高度乘积之和，表示所有高度的中心。
• 二阶中心矩：表示所有点的高度波动范围。

2、矩的数学意义

数学上，矩是一组点组成的模型的特定的数量测度。

定义：设 $X$ 和 $Y$ 是离散随机变量，$c$ 为场数，$k$ 为正整数，

如果 $E(|X-c{|}^k)$ 存在，则称 $E(|X-c{|}^k)$ 为 $X$ 关于点 $c$ 的 $k$ 阶矩。

• $c=0$ 时，称为 $k$ 阶原点矩；
• $c=E(X)$ 时，称为 $k$ 阶中心距。

如果 $E(|X-c_1{|}^p\cdot |Y-c_2{|}^q)$ 存在，则称其为 $X,Y$ 关于 $c$ 点的 $p+q$ 阶矩。

• $c_1=c_2=0$ 时，称为 $p+q$ 阶混合原点矩；
• $c_1=E(X),c_2=E(Y)$ 时，称为 $p+q$ 阶混合中心矩。

如果 $X,Y$ 是连续型变量，则 ${\int }_k(X-c{)}^{k}dx$ 称为 $X$ 关于点 $c$ 的 $k$ 阶原点矩，$\int {\int }_{p+q}(X-x_0{)}^p\cdot (Y-y_0{)}^{q}dxdy$ 称为 $X,Y$ 关于点 $c$ 的 $p+q$ 阶混合中心距。

2.1、期望

随机变量的期望定义为其一阶原点矩：
$$E(x)={\int }_{-\infty }^{+\infty }xf(x)dx$$
在方差等概念定义中，期望也被称为随机变量的中心。显然，任何随机变量的一阶中心矩为 $0$，一阶中心矩的计算公式如下：
$${\int }_{-\infty }^{+\infty }(x-c)f(x)dx$$
对于二阶及更高阶的矩，通常使用中心矩(围绕平均值 $c$ 的矩，均值是一阶矩)，而不是原点矩。因为中心矩更能体现分布形状的信息。

2.2、方差

随机变量的方差定义为其二阶中心矩：
$$Var(x)={\int }_{-\infty }^{+\infty }(x-c{)}^{2}f(x)dx$$

2.3、归一化矩

归一化 $n$ 阶中心矩或者说标准矩，是 $n$ 阶中心矩除以标准差 ${\delta }^n$，归一化 $n$ 阶中心矩为:
$$x=\frac{E[(x-\mu {)}^n]}{{\delta }^n}$$
这些归一化矩是无量纲值，表示独立于任何尺度的线性变化的分布。

2.4、偏态

随机变量的偏态(衡量分布不对称性)定义为其三阶中心矩：
$$S(x)={\int }_{-\infty }^{+\infty }[x-E(x){]}^{3}f(x)dx$$
需要注意的是，任何对称分布的偏态为 $0$，归一化三阶矩被称为偏斜度：

• 向左偏斜，分布尾部在左侧较长，具有负偏度，失效率数据常向左偏斜，如极少量的灯泡会立即烧坏。
• 向右偏斜，分布尾部在右侧较长，具有正偏度，工资数据往往以这种方式偏斜，大多数人所得工资较少。

2.5、峰度

一般随机变量的峰度定义为其四阶中心矩与方差平方的比值再减 3 ，减 $3$ 是为了让正态分布峰度为 $0$，这也被称为超值峰度：
$$K(x)=\frac{{\int }_{-\infty }^{+\infty }[x-E(x){]}^{4}f(x)dx}{{\delta }^2}-3$$
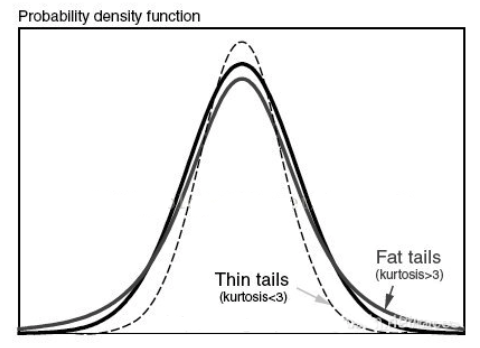
峰度表示分布的波峰和尾部与正态分布的区别，峰度有助于初步了解数据分布的一版特征。

完全符合正态分布的数据峰度值为 $0$，且正态分布曲线被称为基线。如果样本峰度显著偏离 $0$，就可判断此数据不是正态分布。

3、矩的应用

如今矩技术已广泛应用于图像检索和识别 、图像匹配 、图像重建 、数字压缩 、数字水印及运动图像序列分析等领域。常见的矩描述子可以分为以下几种：

• 几何矩
• 正交矩
• 复数矩
• 旋转矩。

3.1、图像矩

在图像处理，计算机视觉和相关领域中，一个图像矩是图像像素强度的某个特定加权平均（矩），或者是这样的矩的函数，通常选择具有一些有吸引力的特性或解释。图像矩对于分割之后对象的描述是有用的。通过图像矩得到的图像的简单属性包括面积（或总强度），其质心和关于其方向的信息。

对于图像来说，零阶矩表示一团像素的像素值之和，公式如下：
$$M_{00}=\sum _I\sum _{J}V(i,j)$$
一阶矩表示横坐标和对应像素值的乘积和纵坐标和对应像素值的乘积，公式如下：
$$M_{10}=\sum _I\sum _{J}i\cdot V(i,j)$$

$$M_{01}=\sum _I\sum _{J}j\cdot V(i,j)$$

3.2、图像的面积和质心：

对于求解图像的面积和质心，我们的应用场景通常是对各个contours进行求解，所以如果前景像素为 $1$，背景像素为 $0$ 的情况，$M_{00}$ 就是所求的contour的面积，质心的公式如下：
$$x_c=\frac{M_{10}}{M_{00}},y_c=\frac{M_{01}}{M_{00}}$$