需求：无

本篇文章将解决一下几个问题：

1. 队列是什么？
2. 如何实现一个队列？
3. 什么场景下会用队列？

 队列的概念：

• 队列：一种只允许一端进行插入数据操作，在另一端进行删除操作的特殊线性表。队列具有先进先出（FIFO）入队列：进行插入操作的一端称为队尾，出队列的一端叫做队头。

 队列的实现：

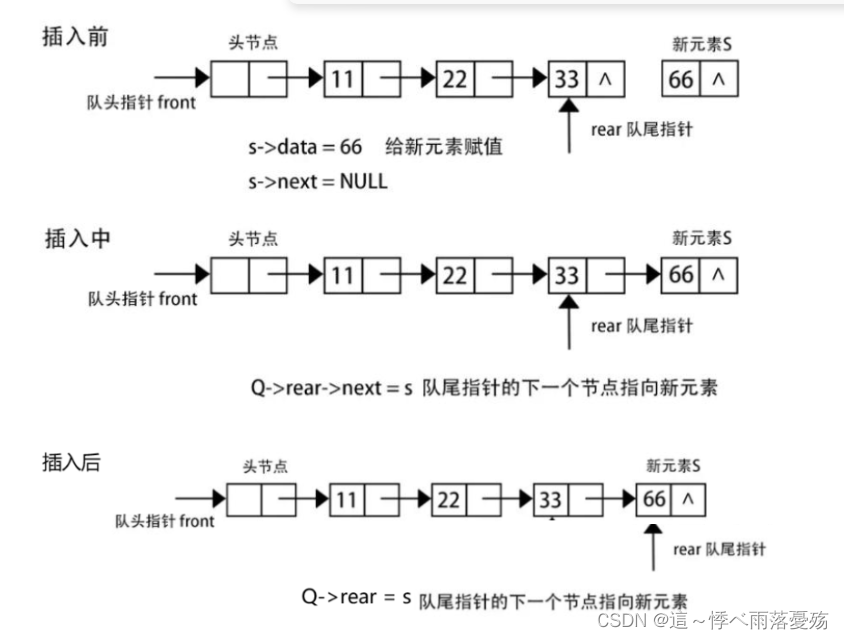
•  队列也可以使用链表或者数组来实现。但是一般都是用链表来实现，如果用数组的话，出队列的时候，会移动数据，效率很低（O（N））。
• 用链表实现，出队列时要记录好头节点的下一个节点。

• 队列的判空：当元素个数为0，就是一个空队列，这时不允许出队列。

• 队列元素的个数：当入队列的时候，size就+1，出队列时就-1，当我们需要元素个数的时候就不需要遍历，用O（1）的时间复杂度就可以完成队列的元素个数。

 队列的应用场景：

•  其实在我们的生活中，到处都是队列的身影，像排队买票的时候，医院叫号的时候....
• 还有就是想大麦app上抢演唱会的票等等，都有队列的身影。

队列的源码：

void QueueInit(Queue* pq)
{assert(pq);pq->tail = pq->head = NULL;pq->size = 0;
}void QueueDestroy(Queue* pq)
{assert(pq);QueueNode* cur = pq->head;while (cur){QueueNode* next = cur->next;free(cur);cur = next;}
}void QueuePush(Queue* pq, QueueDateType x)
{assert(pq);QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->next = NULL;newnode->val = x;if (pq->head == NULL){pq->tail = pq->head = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;pq->size--;}else{QueueNode* next = pq->head->next;free(pq->head);pq->head = next;pq->size--;}
}QueueDateType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->val;
}QueueDateType QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->val;
}int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL;
}void QueuePrint(Queue* pq)
{assert(pq);while (pq->head){printf("%d ", pq->head->val);pq->head = pq->head->next;}printf("\n");
}

typedef int QueueDateType;
typedef struct QueueNode
{struct QueueNode* next;QueueDateType val;
}QueueNode;typedef struct Queue
{QueueNode* head;QueueNode* tail;int size;
}Queue;void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq,QueueDateType x);
void QueuePop(Queue* pq);
QueueDateType QueueFront(Queue* pq);
QueueDateType QueueBack(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);
void QueuePrint(Queue* pq);