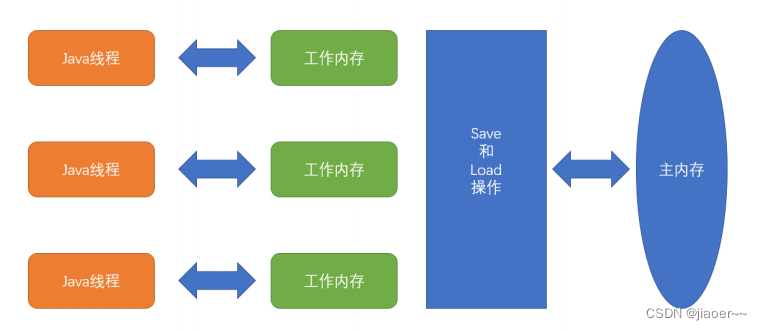
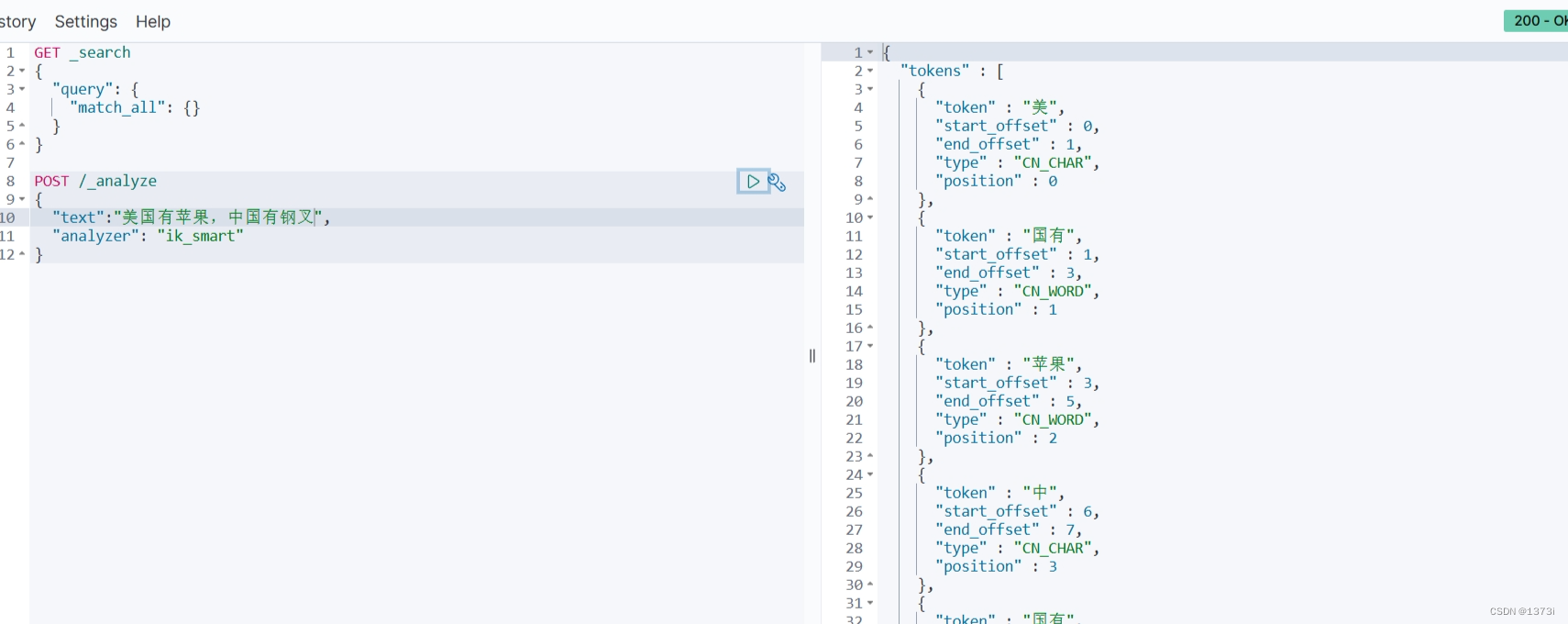
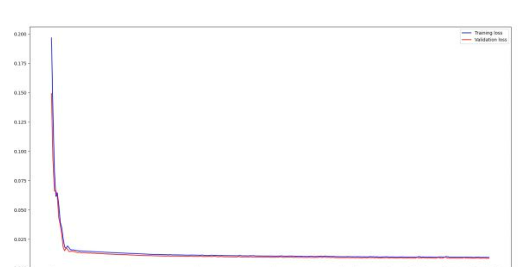
2-3查找树
2-结点:含有一个键(及其对应的值)和两条链,左链接指向2-3树中的键都小于该结点,右链接指向的2-3树中的键都大于该结点。
3-结点:含有两个键(及其对应的值)和三条链,左链接指向的2-3树中的键都小于该结点,中链接指向的2-3树中的键都位于该结点的两个键之间,右链接指向的2-3树中的键都大于该结点。
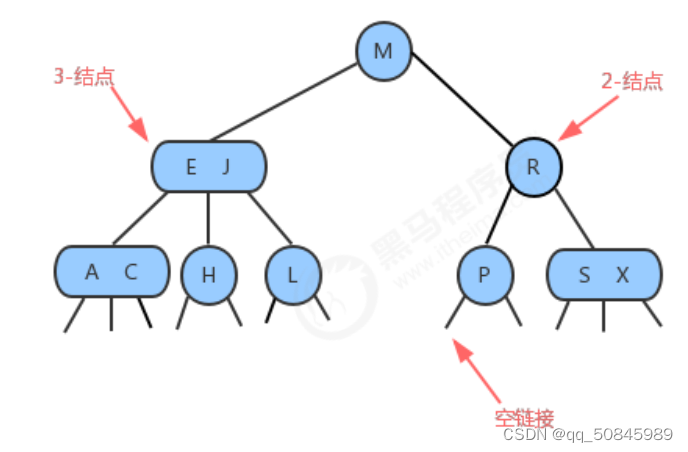
查找:判断一个键是否在树中,先和根节点的键比较,如果相等,查找命中,如果不同,根据比较结果,在其子树中继续查找。还是空连接,查找未命中。
插入:
1.向2-结点插入:首先进行查找,将结点挂载未找到的结点上,如果未找到的结点是一个2-结点,将新元素放到里面变成3-结点。
2.向3-结点插入:将元素放入3-节点,变成4-结点,将4-结点中间元素提升,小于中间元素作为左节点,大于中间元素作为右结点。树的高度加1。
3.向父节点为2-结点,子结点为3-结点中插入:将元素插入3-结点中,变成临时的4-结点。将结点中的中间元素提升到2-结点中,父节点从2-结点变成3-结点,将左右元素挂载到适当的位置。
4.向父子结点为3-结点中插入:将元素插入子结点3-结点中,变成临时的4-结点。提升中间元素将父节点从3-结点变成4-结点,将左右元素放到适当位置。将父节点中的中间元素提升,直到遇到一个父节点是2-结点,将其变成3-结点为止,就可以了。
5.当插入时,所有结点都是3-结点时,将根节点变成一个临时4-结点,将根节点拆分成两个2-结点。树高度+1.
性质:
1.任意空链接到根结点的路径长度都是相等的。
2. 4-结点变换为3-结点时,树的高度不会发生变化,只有当根结点是临时的4-结点,分解根结点时,树高+1。
3. 2-3树与普通二叉查找树最大的区别在于,普通的二叉查找树是自顶向下生长,而2-3树是自底向上生长。
直接实现2-3查找树较为复杂,但是其概念有利于红黑树、B树、B+树。