一.图的定义和分类
定义:图是由一组顶点和一组能够将两个顶点连接的边组成的。
特殊的图:
1.自环:即一条连接一个顶点和其自身的边;
2.平行边:连接同一对顶点的两条边;
图的分类:
按照连接两个顶点的边的不同,可以把图分为以下两种:
无向图:边仅仅连接两个顶点,没有其他含义;
有向图:边不仅连接两个顶点,并且具有方向;
二.无向图
1.图的相关术语
相邻顶点:
当两个顶点通过一条边相连时,我们称这两个顶点是相邻的,并且称这个边依赖于这两个顶点。
度:
某个顶点的度就是依附于该顶点的边的个数。
子图:
是一幅图的所有边的子集(包含这些边依附的顶点)组成的图。
路径:
是由边顺序连接的一系列的顶点组成。
环:
是一条至少含有一条边且终点和起点相同的路径。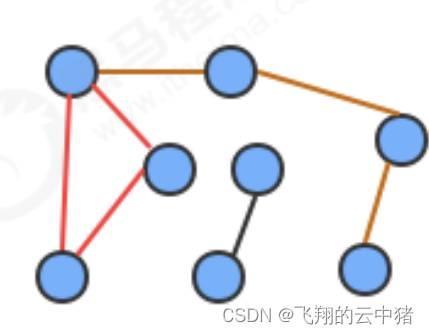
连通图:
如果图中任一一个顶点都存在一条路径到达另外一个顶点,那么这幅图就称之为联通图。
连通子图:
一个非联通图由若干连通的部分组成,每一个连通的部分都可以成为该图的连通子图。

2.图的存储结构
要表示一幅图,只需要表示清楚一下两部分内容即可:
1.图中所有的顶点;
2.所有连接顶点的边;
常见 图的存储结构有两种:邻接矩阵和邻接表
【1】邻接矩阵
1.使用一个V*V的二维数组int[V][V] adj。
2.如果顶点v和顶点w相连,我们只需要把adj[v][w]和adj[w][v]的值设置为1,否则设置为0即可。
很明显,邻接矩阵这种存储方式的空间复杂度是V^2的,如果我们处理的问题规模比较大的话,内存空间极有可能不够用。
【2】邻接表
1.使用一个大小为V的数组Queue[V] adj,把索引看做是顶点;
2.每个索引处adj[v]存储了一个队列,该队列中存储的是所有与该顶点相邻的其他顶点
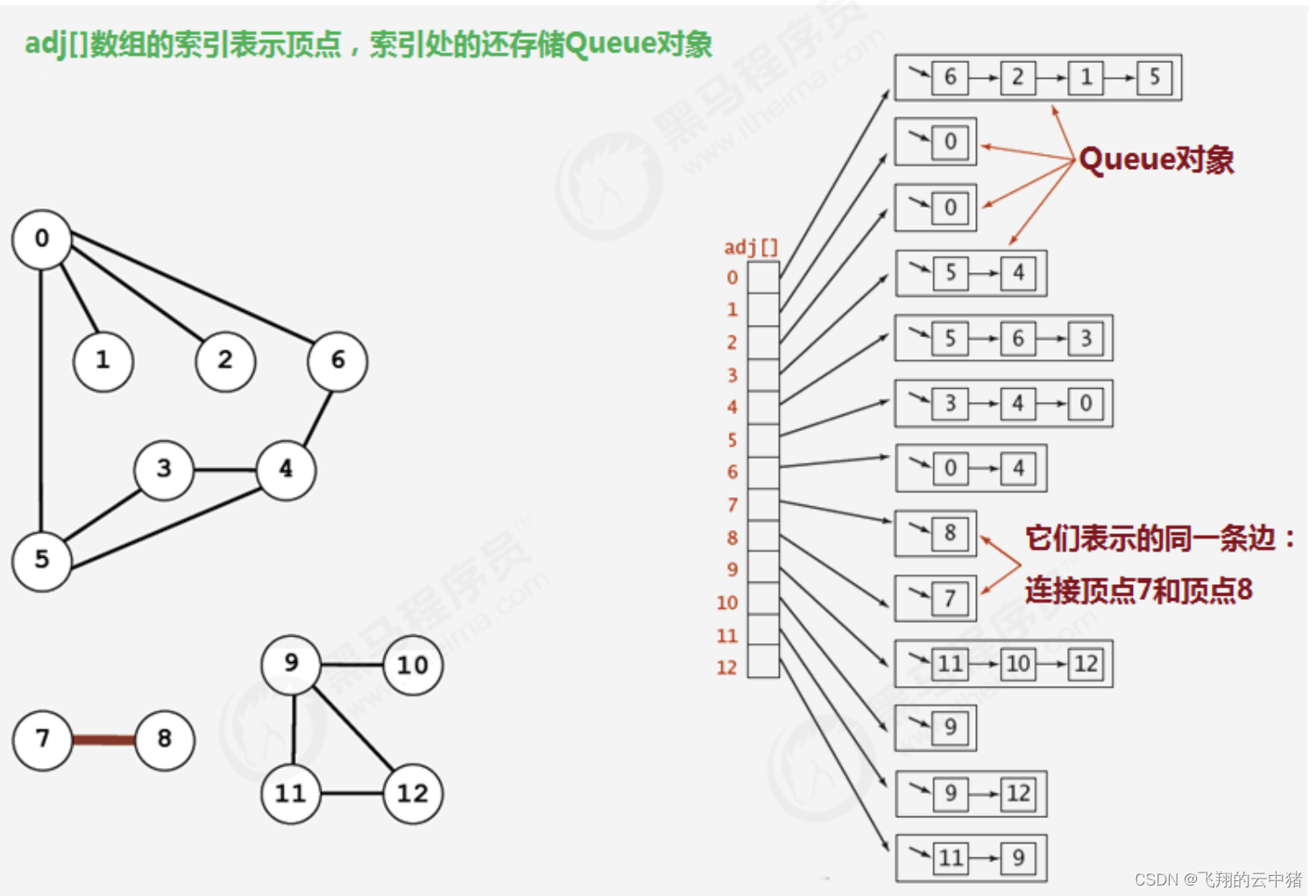
很明显,邻接表的空间并不是是线性级别的,所以后面我们一直采用邻接表这种存储形式来表示图。
三.图的实现

四.图的搜索
1.深度优先搜索
所谓的深度优先搜索,指的是在搜索时,如果遇到一个结点既有子结点,又有兄弟结点,那么先找子结点,然后找 兄弟结点。
2.广度优先搜索
所谓的广度优先搜索,指的是在搜索时,如果遇到一个结点既有子结点,又有兄弟结点,那么先找兄弟结点,然后 找子结点。
![java八股文面试[java基础]——异常](https://img-blog.csdnimg.cn/c0a4aea23c394ca6aa3085108a5c508d.png)