纯C语言实现（小白也能看明白）

题目

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内。

请不要使用除法，且在 O(n) 时间复杂度内完成此题。

难度：中等

题目链接：238. 除自身以外数组的乘积

解题思路 

由于该题不能使用除法 所以参考题解写一个左右乘积列表的方法 创建两个新的数组a,b 一个用于记录从左到右的乘积（类似于动态规划的思想）a 另一个记录从右到左的乘积 b（注意b是从右到左进行累乘） 而a的最左端为1，b的最右端为1 如此在结尾的时候只需要a*b即可 举例， ans[0]=a[0]*b[0] a[0]=1 b[0]=除了nums[0]以外所有元素的乘积

代码展示 

/*** Note: The returned array must be malloced, assume caller calls free().*/
int* productExceptSelf(int* nums, int numsSize, int* returnSize){//前缀积*后缀积 == 除自身以外数组的乘积int *answer = (int*)malloc(sizeof(int)*numsSize);answer[0] = 1;//第一个数字前面没有数字了，第一个数字的前缀是1int i = 0;//前缀积for(i = 1;i<numsSize;i++){answer[i] = answer[i-1]*nums[i-1];}//后缀积int rp[numsSize];//用来记录后缀积rp[numsSize-1] = 1;//因为最后边的数的后缀只能是1for(i = numsSize -1-1;i>=0;i--){rp[i] = rp[i+1] * nums[i+1]; }for(i = 0;i<numsSize;i++){answer[i] = answer[i] * rp[i];//前缀积*后缀积}*returnSize = numsSize;//返回数组的大小return answer;//返回数组answer
}

 【超详细解析】

首先这是一个函数功能实现，一定要注意函数的参数。(int * nums ,这是传的是数组的地址，numsSize，这是数组的大小，*numsSize ,是要返回使用后数组的大小)

接下来是 代码分析

因为 根据题目的意思 我们要返回数组answer ，可以使用malloc()动态分配内存空间

int *answer = (int*)malloc(sizeof(int)*numsSize);

这行代码的意思是：创建了一个指针变量 answer，并使用 malloc() 函数动态分配了一块内存空间，大小为 sizeof(int)*numsSize 字节。其中，sizeof(int) 是指 int 类型在当前系统中所占据的字节数，numsSize 是一个变量，表示需要分配的元素个数。通过将 malloc() 返回的内存地址强制类型转换为 int*，将其赋值给指针变量 answer。这样就可以在动态分配的内存空间中存储 numsSize 个整数。

题目的意思 计算除自身以外数组的乘积，我们根据解题思路，采用 结果 == 前缀积 * 后缀积

就比如 1 2 3 4 5，这里 我采取除3以外数组的乘积（1*2*4*5），因为题目要求不要使用除法，且在 O(n) 时间复杂度内完成此题。所以 （1*2*4*5）变为 1*2 ( 前缀积)  * 4*5（后缀积），

这样 （1*2）*（4*5）

前缀积

这里我们以数组 [1，2，3，4] , 这里我们需要注意的是 数组的第一个元素的前缀乘积和数组的最后一个元素的后缀乘积是1。我们用answer数组来接收

answer[0] = 1;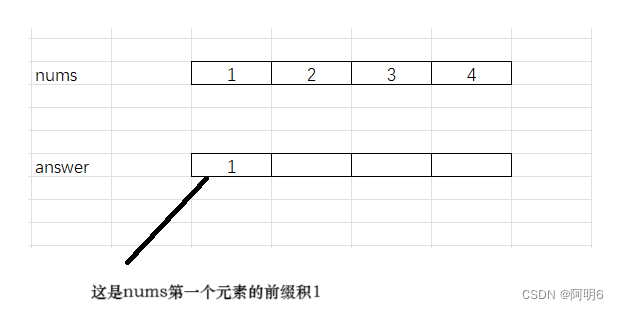

（虽然answer数组要返回结果，我们可以先使用得到前缀之积，再借助另一个数组得到后缀之积，然后两数组各个元素相乘得到结果。这样就可一个减少一定的内存消耗）

接下里求前缀积（因为我们知道数组第一个元素的前缀之积是1）故从第二个元素开始计算

    //前缀积for(i = 1;i<numsSize;i++){answer[i] = answer[i-1]*nums[i-1];}

接下来要求的是nums[1] 即第二个元素的前缀积

 

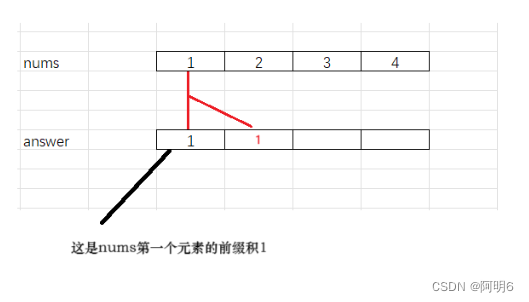
因为nums[1]  前面只有一个元素就是 1 故nums[1] 的前缀积 是1

再看nums[2]

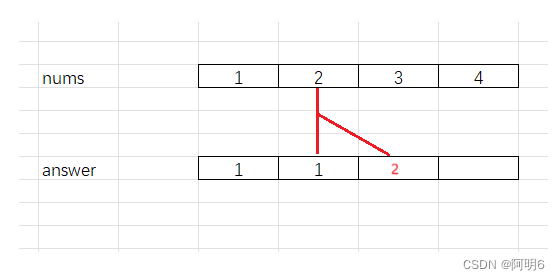
 这时你可能有这样的疑问 为什么要 nums[1]*answer[1] 而不是 nums[0] * nums[1] 呢

这里你需要知道 乘积 肯定时连乘的 ，可以这样理解 answer数组 里面存放 的每一个阶段的乘积（其实就是每个nums数组对应的前缀的乘积）

nums[3]

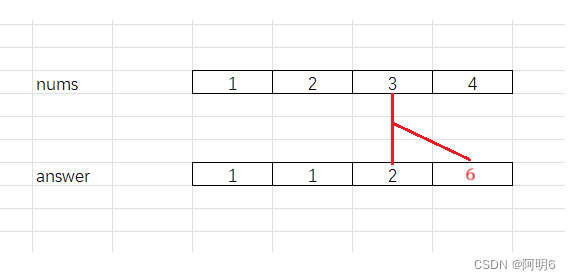
 后缀乘积

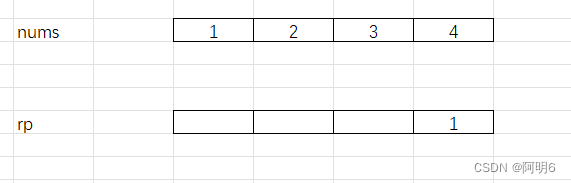
    //后缀积int rp[numsSize];//用来记录后缀积rp[numsSize-1] = 1;//因为最后边的数的后缀只能是1for(i = numsSize -1-1;i>=0;i--){rp[i] = rp[i+1] * nums[i+1]; }

这提前声明了一个rp数组用来记录后缀积，数组最后的一个元素的后置缀之积 是1

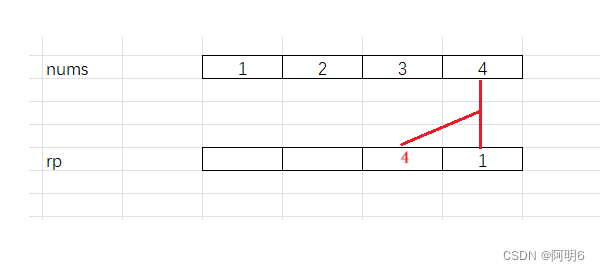
rp[1]

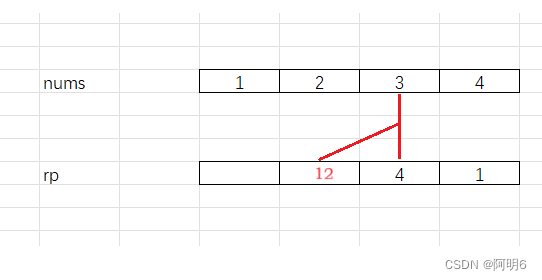
 rp[2]

rp[3]

前缀积*后缀积

    for(i = 0;i<numsSize;i++){answer[i] = answer[i] * rp[i];//前缀积*后缀积}

最后 answer数组与rp数组对应元素做乘积（answer[i] = answer[i] * rp[i]）

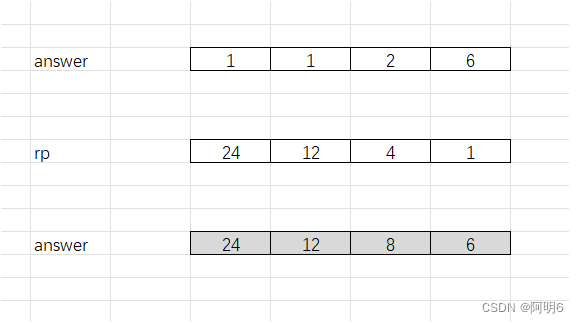
 这的answer数组的大小与 nums 的数组大小一致 返回 numsSize ，数组返回 answer