LeetCode538. 把二叉搜索树转换为累加树

538. 把二叉搜索树转换为累加树

文章目录

- - [538. 把二叉搜索树转换为累加树](https://leetcode.cn/problems/convert-bst-to-greater-tree/)
  - - 一、题目
    - 二、题解
    - - 方法一：递归（中序遍历与节点更新）
      - 方法二：反向中序遍历与累加更新：更简洁的解法
      - 方法三：迭代（反向中序遍历）

一、题目

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。

示例 1：

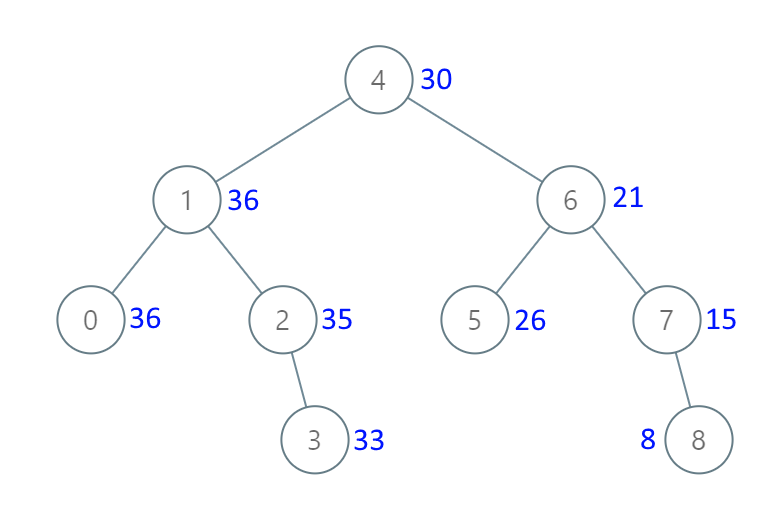
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

树中的节点数介于 0 和 104 之间。
每个节点的值介于 -104 和 104 之间。
树中的所有值 互不相同 。
给定的树为二叉搜索树。

二、题解

方法一：递归（中序遍历与节点更新）

针对这个问题，我们可以考虑通过中序遍历来获取有序的节点值，然后从大到小更新节点的值，以满足累加树的要求。

算法思路

创建一个空的向量 array 用于存储中序遍历得到的有序节点值。
执行中序遍历函数 traversal_vec(root, array)，该函数会将二叉搜索树的节点值按照从小到大的顺序存储在 array 中。
从 array 的倒数第二个元素开始，将每个元素与其后一个元素相加，以便得到累加和。这一步保证了在累加树中，每个节点的值等于原树中大于或等于该节点值的所有节点值之和。
执行函数 traversal_res(root, array)，该函数会将更新后的累加和值赋给二叉搜索树的每个节点。
返回更新后的二叉搜索树。

具体实现

以下是对每个步骤的详细实现：

class Solution {
public:int i = 0;// 中序遍历获取有序节点值并存储在array中void traversal_vec(TreeNode *root, vector<int> &array){if(root == nullptr) return;traversal_vec(root->left, array);array.push_back(root->val);traversal_vec(root->right, array);}// 更新节点值为累加和void traversal_res(TreeNode *root, vector<int>& array){if(root == nullptr) return;traversal_res(root->left, array);root->val = array[i++];traversal_res(root->right, array);}TreeNode* convertBST(TreeNode* root) {if(root == nullptr) return nullptr;vector<int> array;// 获取有序节点值traversal_vec(root, array);// 计算累加和for(int j = array.size() - 2; j >= 0; j--){array[j] += array[j+1];}// 更新节点值为累加和traversal_res(root, array);return root;}
};

或者将i作为参数传入traversal_res()也行：

class Solution {
public:void traversal_vec(TreeNode *root, vector<int> &array) {if (root == nullptr) return;traversal_vec(root->left, array);array.push_back(root->val);traversal_vec(root->right, array);}int traversal_res(TreeNode *root, int i, const vector<int> &array) {if (root == nullptr) return i;i = traversal_res(root->left, i, array);root->val = array[i];i++;i = traversal_res(root->right, i, array);return i;}TreeNode* convertBST(TreeNode* root) {if (root == nullptr) return nullptr;vector<int> array;traversal_vec(root, array);for (int j = array.size() - 2; j >= 0; j--) {array[j] += array[j + 1];}traversal_res(root, 0, array);return root;}
};

算法分析

时间复杂度：算法的时间复杂度主要由两个部分构成：中序遍历和更新节点值。中序遍历需要访问每个节点一次，而更新节点值也需要访问每个节点一次。因此，算法的时间复杂度为 O(N)，其中 N 是节点的数量。
空间复杂度：算法的空间复杂度主要由中序遍历时存储节点值的数组 array 所占用的空间。在最坏的情况下，数组的大小为 N，因此空间复杂度为 O(N)。除此之外，递归调用栈也会占用一些空间，但是在二叉搜索树的情况下，递归调用栈的最大深度不会超过树的高度，因此额外空间的使用不会超过 O(log N)。

方法二：反向中序遍历与累加更新：更简洁的解法

算法思路

这个算法采用了一种不同的方法来实现二叉搜索树到累加树的转换。通过反向中序遍历（从右子树到左子树），我们可以更方便地得到大于当前节点值的节点值之和，然后直接更新节点值，从而获得累加树。

具体实现

class Solution {
public:// 反向中序遍历并更新节点值void convertBSTHelper(TreeNode* root, int& sum) {if(root == nullptr) return;convertBSTHelper(root->right, sum); // 先处理右子树sum += root->val; // 更新累加和root->val = sum; // 更新节点值convertBSTHelper(root->left, sum); // 处理左子树}TreeNode* convertBST(TreeNode* root) {if(root == nullptr) return nullptr;int sum = 0;convertBSTHelper(root, sum);return root;}
};

算法分析

时间复杂度：算法的时间复杂度主要由中序遍历和更新节点值组成。每个节点都会被访问一次且只访问一次，因此时间复杂度为 O(N)，其中 N 是节点的数量。
空间复杂度：算法的空间复杂度由递归调用栈所占用的空间决定。在二叉搜索树的情况下，递归调用栈的最大深度不会超过树的高度，因此额外空间的使用不会超过 O(log N)。

方法三：迭代（反向中序遍历）

算法思路

这个算法采用了反向中序遍历的方式，通过栈来实现，来构建累加树。遍历的过程中，我们从最大值开始，逐步向较小值移动，同时将大于等于当前节点值的所有节点值累加起来，然后将该累加值赋予当前节点，最终构建出累加树。

具体实现

class Solution {
private:int previousValue; // 记录前一个节点的值// 反向中序遍历并更新节点值void reverseInorderTraversal(TreeNode* root) {stack<TreeNode*> nodeStack;TreeNode* current = root;while (current != nullptr || !nodeStack.empty()) {if (current != nullptr) {nodeStack.push(current);current = current->right; // 右子树} else {current = nodeStack.top(); // 弹出栈顶节点nodeStack.pop();// 更新节点值current->val += previousValue;previousValue = current->val;current = current->left; // 左子树}}}public:TreeNode* convertBST(TreeNode* root) {previousValue = 0; // 初始化前一个节点的值reverseInorderTraversal(root); // 反向中序遍历更新节点值return root;}
};