1.非负 ODE 解
本博客说明如何将 ODE 解约束为非负解。施加非负约束不一定总是可有可无,在某些情况下,由于方程的物理解释或解性质的原因,可能有必要施加非负约束。仅在必要时对解施加此约束,例如不这样做积分就会失败或者解将不适用的情况。
如果解的特定分量必须为非负,则使用 odeset 来设置这些分量的索引的 NonNegative 选项。此选项不适用于 ode23s 、 ode15i ,也不适用于用来求解涉及质量矩阵的问题的隐式求解器( ode15s 、 ode23t、ode23tb )。特别是,不能对 DAE 问题施加非负性约束,DAE 问题一定有奇异质量矩阵。
1.1 示例:绝对值函数
考虑初始值问题
y′ = − | y |,
该问题使用初始条件 y (0) = 1 在区间 [0, 40] 上求解。此 ODE 的解将衰减到零。如果求解器生成负解值,则它会开始通过此值来跟踪 ODE 的解,随着计算得出的解逐渐发散为 − ࣛ,计算最终会失败。使用NonNegative 选项可防止此积分失败。
将 y ( t ) =  的解析解分别与使用不带额外选项的 ode45 得出的 ODE 解和设定 NonNegative 选项时得出的 ODE 解进行比较。
的解析解分别与使用不带额外选项的 ode45 得出的 ODE 解和设定 NonNegative 选项时得出的 ODE 解进行比较。
ode = @(t,y) -abs(y);
% Standard solution with |ode45|
options1 = odeset('Refine',1);
[t0,y0] = ode45(ode,[0 40],1,options1);
% Solution with nonnegative constraint
options2 = odeset(options1,'NonNegative',1);
[t1,y1] = ode45(ode,[0 40],1,options2);
% Analytic solution
t = linspace(0,40,1000);
y = exp(-t);
% 绘制这三个解进行比较。施加非负约束对于防止解向 − ࣛ 发展至关重要。
plot(t,y,'b-',t0,y0,'ro',t1,y1,'k*');
legend('Exact solution','No constraints','Nonnegativity', ...
'Location','SouthWest')运行结果如下:

1.2 示例:膝盖问题
另一个要求非负解的问题示例是在示例文件 kneeode 中编码的膝盖问题。方程是:
ϵy′ = (1 − x)y − y^ 2 ,
该问题使用初始条件 y (0) = 1 在区间 [0, 2] 上求解。通常采用参数 ϵ 以满足 0 < ϵ ԟ 1,并且此问题使用ϵ = 1 × 10^( −6) 。此 ODE 的解在 x < 1 时趋近于 y = 1 − x ,在 x > 1 时趋近于 y = 0。但通过使用默认容差计算数值解可以看到,解在整个积分区间中遵循 y = 1 − x 等倾线。施加非负约束会得到正确的解。
在使用和不使用非负值约束两种条件下解算膝盖问题。
epsilon = 1e-6;
y0 = 1;
xspan = [0 2];
odefcn = @(x,y,epsilon) ((1-x)*y - y^2)/epsilon;
% Solve without imposing constraints
[x1,y1] = ode15s(@(x,y) odefcn(x,y,epsilon), xspan, y0);
% Impose a nonnegativity constraint
options = odeset('NonNegative',1);
[x2,y2] = ode15s(@(x,y) odefcn(x,y,epsilon), xspan, y0, options);
% 绘制解进行比较。
plot(x1,y1,'ro',x2,y2,'b*')
axis([0,2,-1,1])
title('The "knee problem"')
legend('No constraints','Non-negativity')
xlabel('x')
ylabel('y')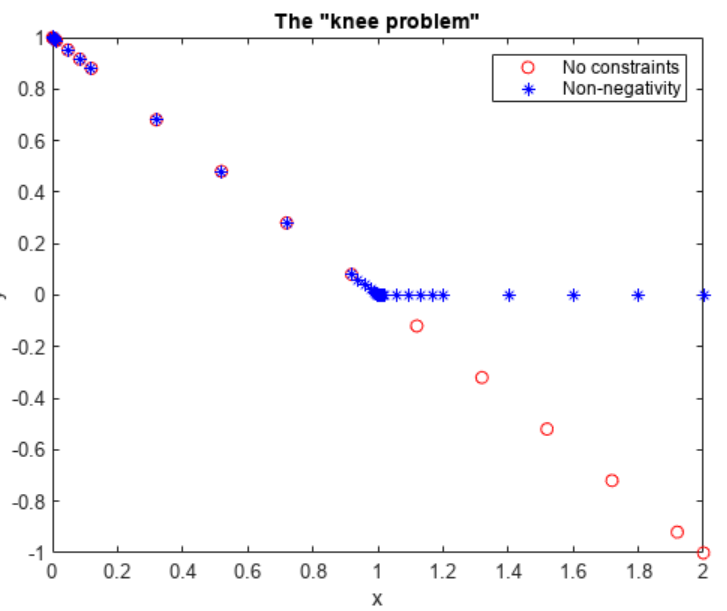
2.常见 ODE 问题及其解答
2.1 误差容限

2.2 问题规模


2.3 DOE的解


2.4 问题类型