【C++】关于fixed和setprecision的学习和介绍

前言

在学习swap函数的时候，偶然了解到了fixed和setprecision，这两条控制语句，在了解了之后，觉得很有用，于是写一篇文章来介绍fixed和setprecision这两条控制语句

fixed控制输出形式

使用fixed语句需要包含<iomanip>头文件

cout<<fixed

那么无论输入的是整数还是浮点数，最终在输出的时候都会是浮点型

下面给出一个例子

#include<iostream>
#include<iomanip>using namespace std;int main()
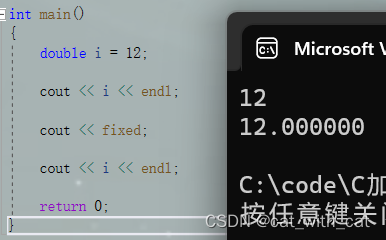
{double i = 12;cout << i << endl;cout << fixed;cout << i << endl;return 0;
}

运行结果
在这里插入图片描述

setprecision语句

使用setprecision语句需要包含<iomanip>头文件
这个语句的作用是，控制输出的数据的精度

语法格式：

cout << setprecision(n);

n就是控制输出的位数

提示；
这里不能输入变量，但是可以输入宏定义的常量或者const修饰的常变量

控制整数位 + 小数位

当并未使用fixed语句时，而是直接使用setprecision语句的话，他计算的位数是整数位 + 小数位

下面给出了一个例子

#include<iostream>
#include<iomanip>using namespace std;int main()
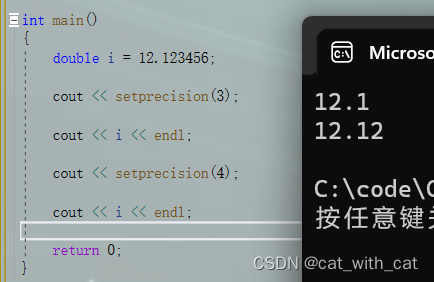
{double i = 12.123456;cout << setprecision(3);cout << i << endl;cout << setprecision(4);cout << i << endl;return 0;
}

运行结果：
在这里插入图片描述

控制小数位

当像下面这么使用时，

cout << fixed << setprecision(n);

在输出时，输出的小数小数点后面就有n位，

下面给出一个例子

#include<iostream>
#include<iomanip>using namespace std;int main()
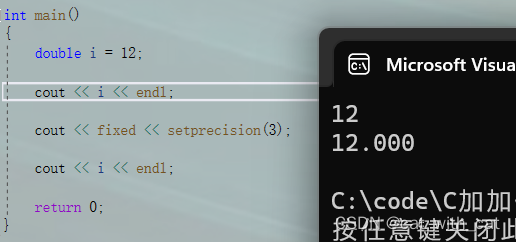
{double i = 12;cout << i << endl;cout << fixed << setprecision(3);cout << i << endl;return 0;
}

运行i结果：

在这里插入图片描述

注意

需要注意的是：这两个控制语句能控制这条语句后面的所有语句，当需要改变时，需要重新写一条语句

并且这两条语句只是控制输出格式，并不会对数据本身造成改变

可以看下面这个个例子，方便理解

#include<iostream>
#include<iomanip>using namespace std;int main()
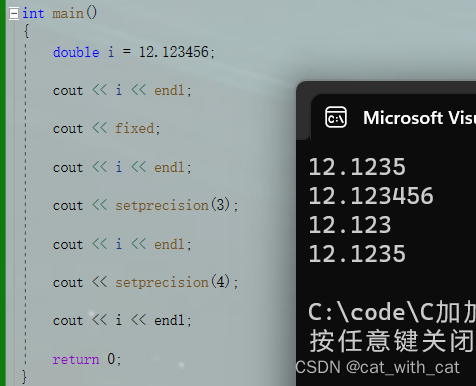
{double i = 12.123456;cout << i << endl;cout << fixed;cout << i << endl;cout << setprecision(3);cout << i << endl;cout << setprecision(4);cout << i << endl;return 0;
}

运行结果：
在这里插入图片描述

练习题

接下来，通过一道题目，来帮助大家更好地去理解fixed和setprecision这两条控制语句

题目:2165: π的火把

七夕节临近，数字王国中的单身狗数字都一个个举起了火把。已知，当数字a举起了b的火把，就变成了a的b次方。那么，如果数字们都举起π的火把会是什么景象呢？

输入

第一行是一个整数T，表示测试实例的个数；

然后是T行输入数据，每行包含两个正整数n和x，表示底数和保留位数。

（1 <= T <= 100，1 <= n <= 500，1 <= x <= 6）

输出

对于每一个n，输出它举起π的火把的样子，输出保留x位数。

样例输入

3
1 3
7 6
9 1

样例输出

1.000
451.807873
995.0

提示

你可以在程序中定义

#define PI acos(-1.0)

思路

首先，这道题的意思是，输入n个整数，分别求这n个整数的PI次方，并给定了精度（也就是输出的位数）

对于输出的位数，我们可以直接使用setprecision这条语句

代码实现

下面就是代码实现

#include<iostream>
#include<iomanip>
#include<cmath>using namespace std;#define pi acos(-1.0);int main()
{int n = 0;int k = 0;int a = 0;int i = 0;double num = 0;cin >> n;for (i = 0; i < n; i++){cin >> a >> k;num = pow(a, pi);cout << fixed << setprecision(k);cout << num;}return 0;
}