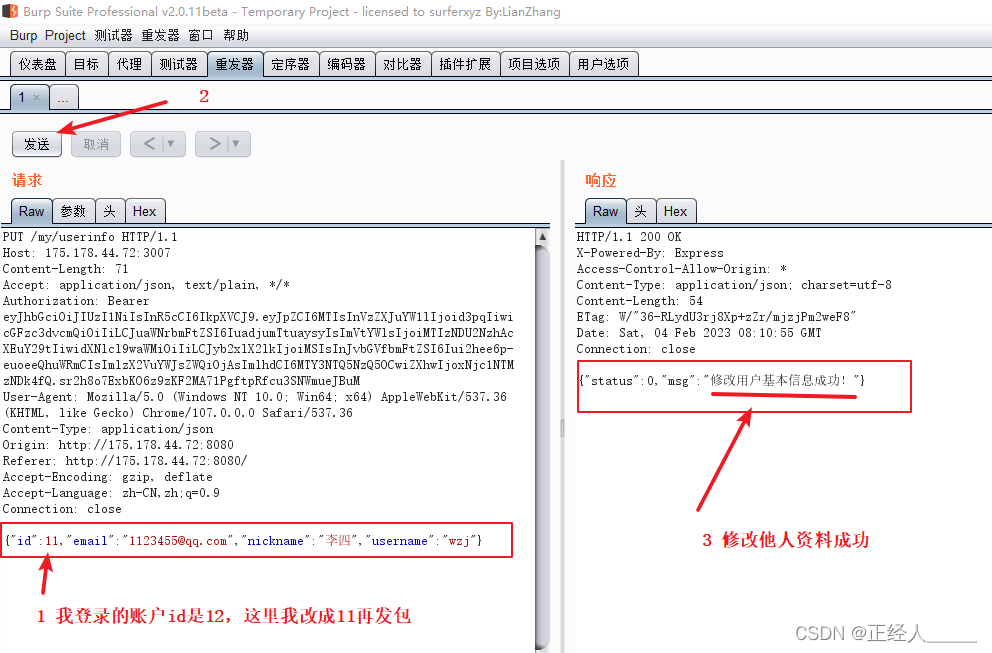
题目：

给你一个整数数组 nums 和一个整数 x 。每一次操作时，你应当移除数组 nums 最左边或最右边的元素，然后从 x 中减去该元素的值。请注意，需要 修改 数组以供接下来的操作使用。

如果可以将 x 恰好 减到 0 ，返回 最小操作数 ；否则，返回 -1 。

示例 1：

输入：nums = [1,1,4,2,3], x = 5
输出：2
解释：最佳解决方案是移除后两个元素，将 x 减到 0 。

示例 2：

输入：nums = [5,6,7,8,9], x = 4
输出：-1

示例 3：

输入：nums = [3,2,20,1,1,3], x = 10
输出：5
解释：最佳解决方案是移除后三个元素和前两个元素（总共 5 次操作），将 x 减到 0 。

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 104
• 1 <= x <= 109

算法原理：

正面入手解题，情况繁杂，一会是取左边一会是取右边，但是正难则反，反面入手解题：

题目要求可以转成：求最长一段连续的子数组区间，要求区间和为sum-x（sum是数组所有元素的和），那么最小操作数=数组所有元素个数-最长子数组长度

题目本来的要求是：求「左端+右端」两段连续的、和为 x 的最短数组

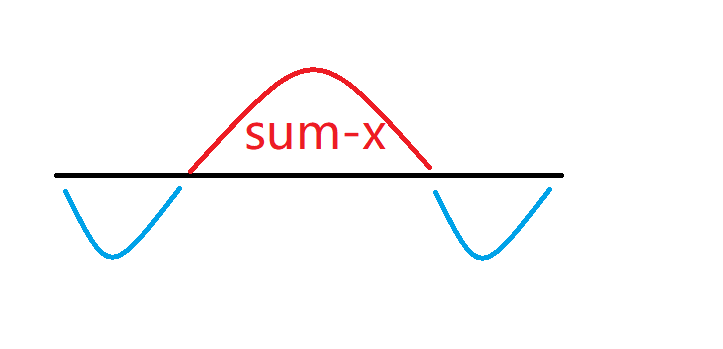
连续区间，可以考虑用滑动窗口来解题

1 求出数组所有元素的和sum 目标值target=sum-x

2 用滑动窗口，找出最长的子数组，使其和为target

   细节：target可能为负数（当sum<x时）但是题目提示中所有元素均不存在负数

             所以返回-1

   left=0（左边界） right=0（指向待进入窗口的元素） sum2统计区间和

   a 进窗口：sum2+=nums[right] 

   b 判断：    若是sum2>target 循环出窗口，直至sum<=target

                     若是循环结束后，sum2==target，则找到一组结果，若此次结果更优则更新结果

   c 出窗口：sum-=nums[left]，left++

代码实现：

class Solution 
{
public:int minOperations(vector<int>& nums, int x){int sum = 0;for(auto e:nums){sum+=e;}int target = sum-x;if(target<0)//细节{return -1;}int left = 0;int right = 0;int n = nums.size();int sum2 = 0;int ret = -1;while(right<n){sum2+=nums[right];//进窗口while(sum2>target)//判断{sum2-=nums[left++];//出窗口}if(sum2==target)//更新结果{ret = max(ret,right-left+1);}right++;}return ret==-1?ret: n-ret;}
};