引言:
树是一种非线性的结构,也是由一个一个的结点构成。
树的一些基本概念:
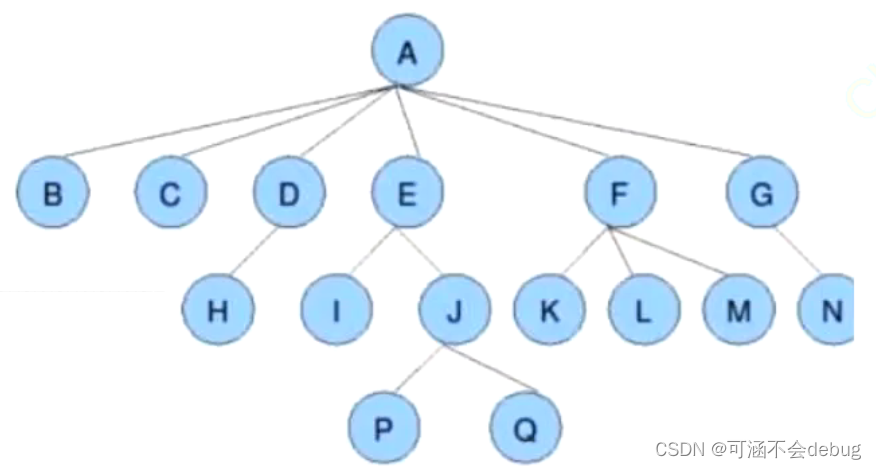
节点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的度为6
叶节点或终端节点:度为0的节点称为叶节点。
非终端节点或分支节点:度不为0的节点;
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。
孩子节点或子节点:如B是A的子节点。
兄弟节点:具有相同父节点的节点互称为兄弟节点
树的度:一棵树中,最大的节点的度称为树的度
节点的层次:从根开始定义,根为第一层,根的子节点是第二层,以此类推。
树的高度或深度:树中节点的最大层次,如上图:树的高度是4.(注意从1开始计数,同时也意味着空树就是0)
树的表示
左孩子右兄弟表示法:

二叉树概念及结构
概念:
- 每个结点最多有两颗子树,即二叉树不存在度大于2 的节点。
- 二叉树的子树有左右之分,其子树的次序不能颠倒。、
二叉树的定义
因为孩子最多有两个,所以直接定义左孩子,右孩子即可。
二叉树的前、中、后序


首先需要明确任何一个二叉树分为3个部分:
- 根节点
- 左子树
- 右子树
注意左子树和右子树都是一个整体,然后从这个整体中再细分根节点、左子树、右子树。
前序(先根):根 左子树 右子树
中序:左子树 根 右子树
后序:左子树 右子树 根
这个前中后的顺序是根据根的位置而决定的

下面是前、中、后序的原码(利用递归去求解)
void PrevOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%c ", root->val);PrevOrder(root->left);PrevOrder(root->right);
}void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%c ", root->val);InOrder(root->right);
}void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%c ", root->val);
}
特殊的二叉树

- 满二叉树:一个二叉树,如果每一个层的结点树都达到最大值,就称为满二叉树
- 完全二叉树:就是在满二叉树的基础上,前h-1层都是满的,但是最后一层不满,但是最后一层从左往右都是连续的。
二叉树的性质
- 如果规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点。
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点个数(也就是满二叉树的个数)是2^h-1
- 对任何一棵二叉树,如果度为0的叶节点的个数为n0,度为2的分支结点的个数为n2,则有n0 = n2+1.
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度h = LogN。
根据二叉树的性质进行解题
例题1:

由二叉树的性质3得到叶节点的个数是度为2的分支结点个数+1,所以直接199+1 = 200即可。
例题2:

选择题快速法:
直接假设n = 2,接着进行带入计算,与每个选项进行比较得到正确答案。
常规解法:
设未知数,度为0的结点个数有X0个,度为1的结点个数有X1个,度为2的结点个数有X2个.
就会得到X0+X1+X2 = 2n.
又因为X0和X2的关系X2+1 = X0.
又因为是一个完全二叉树所以度为1结点的个数要么是1要么是0,所以分两种情况,发现当X1 = 1时计算结果是小数,不符合题意,所以X1 = 0得出答案。
例题3:

解答:
假设这棵树的高度是h,假设最后一层缺了X个
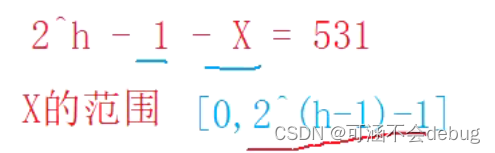
本题也是将选择题的答案带到题目中进行比较,然后得出正确答案。
如何求一棵二叉树中结点的个数?
解法一:
采用循环遍历的思想
遍历这棵树的每一个结点,如果不是空,就size++,否则不进行++。
注意运用这种方法时,因为可能需要计算多颗树的结点,所以每次传参时,需要传一个新的size地址,在主函数中直接打印输出size的值
原码:
void TreeSize(BTNode* root,int* psize)//直接传地址
{if (root == NULL)return;else{(*psize)++;TreeSize(root->left, psize);TreeSize(root->right, psize);}
}
解法二:
采用分治的思想。
何为分治的思想,就是将一个比较复杂的问题进行一层一层的分解,直到分解到简单的层次。将大问题分解为小问题。
例如校长想要统计整个学校的人数,校长将这个任务分配给院长,院长再分配给每个班的班主任,每个班主任再分配给每个宿舍的宿舍长。
本题思路也是如此,统计整棵树的结点个数,将这颗树分为左子树和右子树,左子树再分为小的左子树和小的右子树,层层递归,直到最后一层加1。
原码:
int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;/*if (root == NULL)return 0;else{return TreeSize(root->left) + TreeSize(root->right) + 1;}*/
}如何求二叉树叶子节点的个数?
按照上面分支的思想,咱们举一反三~
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;elsereturn TreeLeafSize(root->left) + TreeLeafSize(root->right);
}TIP:
只需要给出中序+任何一个前序或者后序,就可以将一个完整的二叉树还原出来。
原因:
前序和中序都是知道根节点是哪个,但是并不知道左子树和右子树。
如果有了中序后,并且已知根节点,那么在中序排列中,在根节点的左边就是左子树,在根节点的右边就是右子树,就可以轻松将树还原出来。
关于二叉树的一些经典例题
例题1:二叉树的前序遍历
144. 二叉树的前序遍历 - 力扣(LeetCode)
题目描述:

注意事项:
利用递归的思想去进行前序遍历,注意在递归时,计数器一般需要传址,防止局部变量出生命周期就自动销毁。
假设计数器用全局变量,是不行的。
因为函数接口会被多次调用,全局变量会一直累加!
原码:
//提前计算好树的结点的个数,方便创建动态数组的个数
int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}void _PrevOrder(struct TreeNode* root,int* arr,int* pcnt)
{//前序递归遍历,将遍历的结点存储到动态数组中if(root == NULL)return;arr[*pcnt] = root->val;(*pcnt)++;_PrevOrder(root->left,arr,pcnt);_PrevOrder(root->right,arr,pcnt);
}int* preorderTraversal(struct TreeNode* root, int* returnSize){int size = TreeSize(root);int* arr = (int*)malloc(sizeof(int) * size);int cnt = 0;//注意传地址,递归调用一般需要传址操作_PrevOrder(root,arr,&cnt);*returnSize = cnt;return arr;
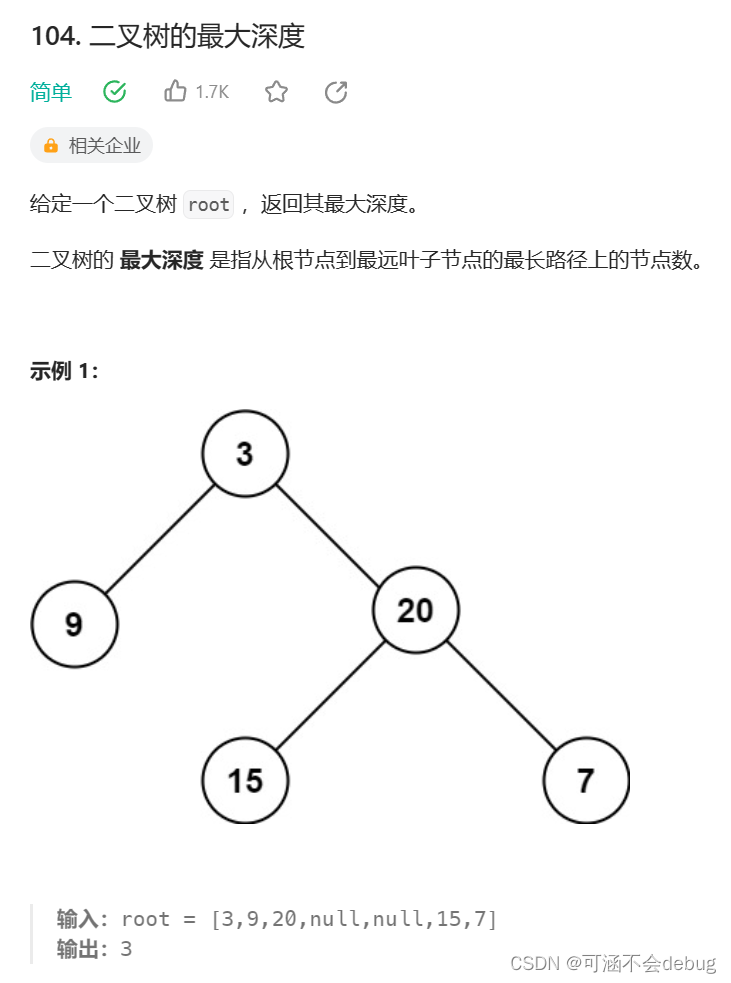
}例题二:二叉树的最大深度
104. 二叉树的最大深度 - 力扣(LeetCode)
题目描述:
解题思路:
同样采用分治的思想,求二叉树的最大深度,就是求左子树和右子树的最大深度,接着继续分治,求左子树中的小左子树和小右子树的最大深度,直到不可分解进行+1即可
原码:
int maxDepth(struct TreeNode* root){if(root == NULL)return 0;int leftmax = maxDepth(root->left) + 1;int rightmax = maxDepth(root->right) + 1;return leftmax > rightmax ? leftmax : rightmax;
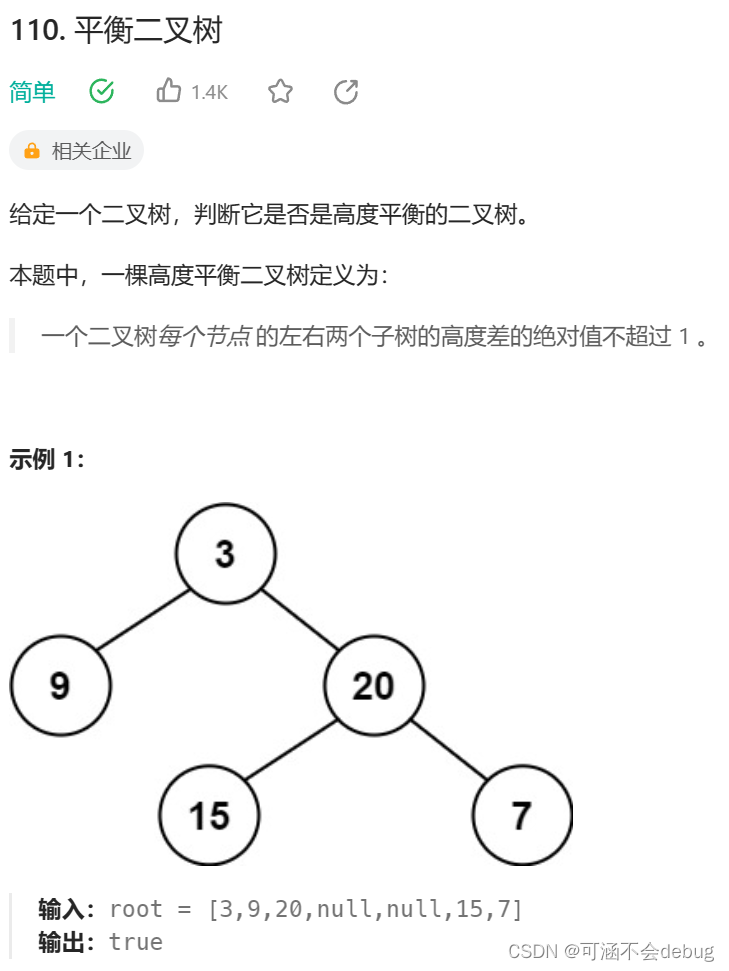
}例题3:判断平衡二叉树
110. 平衡二叉树 - 力扣(LeetCode)
题目描述:
解题思路:
本题要求二叉树的每一个结点都要满足左右两个子树的高度差的绝对值不超过1,所以先判断头结点的左右子树是否满足,如果头结点都不满足,那么直接就返回false。
如果头结点满足,则继续向下递归左右子树的结点是否满足。
原码:
int MaxDepth(struct TreeNode* root)
{if(root == NULL)return 0;int leftDepth = MaxDepth(root->left);int rightDepth = MaxDepth(root->right);return leftDepth > rightDepth ? leftDepth+1 : rightDepth+1;
}bool isBalanced(struct TreeNode* root){if(root == NULL)return true;//先判断头结点,接着再判断子节点int leftDepth = MaxDepth(root->left);int rightDepth = MaxDepth(root->right);return abs(leftDepth-rightDepth) < 2 && isBalanced(root->left) && isBalanced(root->right);
}