Problem - C - Codeforces

题意：

思路：

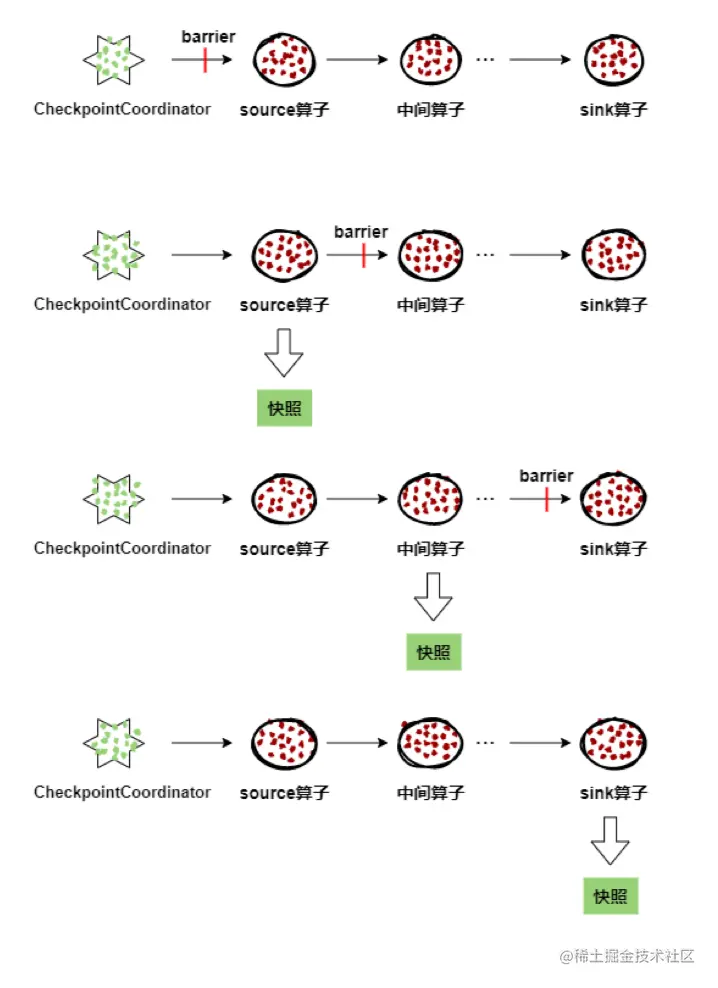
首先，观察样例可知

这种是等效的

推广一下

0000.....111111

..l..............r......

这种是等效的

容易想到维护后面第一个1的位置和前面第一个0的位置，然后把所有区间都等效一下，开一个二元组的set

但是有点问题，考虑一些特殊case

0001111

这样的，很明显等效之后左端点在右端点后面

1

这种的也是

这些特殊case有什么共同点呢？这些区间一个区间sort之后对应一种情况

因此直接插入 {-1， -1}即可

111100000

那么这种呢？等效前和等效后的区间是一样的，直接插入即可

Code：

#include <bits/stdc++.h>#define int long longusing i64 = long long;constexpr int N = 2e5 + 10;
constexpr int M = 2e5 + 10;
constexpr int P = 2600;
constexpr i64 Inf = 1e18;
constexpr int mod = 1e9 + 7;
constexpr double eps = 1e-6;std::string s;int n, m;
int a[N];
int pre0[N];//前面第一个0的位置
int suf1[N];//后面第一个1的位置void solve() {std::cin >> n >> m >> s;s = " " + s;for (int i = 1; i <= n; i ++) {a[i] = s[i] - '0';}pre0[0] = 0;suf1[n + 1] = n + 1;for (int i = 1; i <= n; i ++) {if (a[i] == 0) pre0[i] = i;else pre0[i] = pre0[i - 1];}for (int i = n; i >= 1; i --) {if (a[i] == 1) suf1[i] = i;else suf1[i] = suf1[i + 1];}std::set<std::pair<int,int> > S;for (int i = 1; i <= m; i ++) {int l, r;std::cin >> l >> r;int tl = suf1[l];int tr = pre0[r];if (tl > tr) S.insert({-1, -1});else S.insert({tl, tr});}std::cout << S.size() << "\n";
}
signed main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);int t = 1;std::cin >> t;while (t--) {solve();}return 0;
}