Android 的View动画、属性动画都可以设置动画插值器，以此来实现不同的动画效果。

这篇文章 Android View动画整理有介绍各种插值器的效果，这一篇专访 PathInterpolator 。

参考官网添加曲线动作，

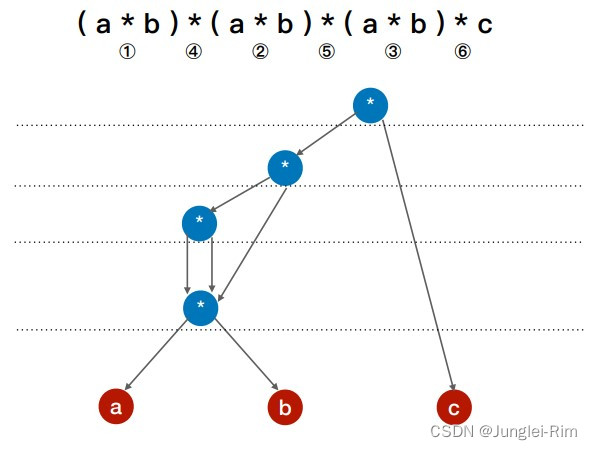
PathInterpolator 基于 贝塞尔曲线 或 Path 对象。此插值器在一个 1x1 的正方形内指定一个动作曲线，定位点位于 (0,0) 和 (1,1)，而控制点则使用构造函数参数指定。

简单来说就是，通过控制点来构造出 (0,0) 到 (1,1) 之间的任意曲线，让动画按照构造出的曲线来执行。

PathInterpolator 和其他动画插值器的使用是一样的，PathInterpolator 的优势是可以创建任意曲线来实现不同的动画效果，劣势是比较难绘制出满意的曲线，毕竟涉及了数学公式。

贝塞尔曲线

贝塞尔曲线的相关说明：
贝塞尔曲线_百度百科
从零开始学图形学：10分钟看懂贝塞尔曲线
曲线篇: 贝塞尔曲线

贝塞尔曲线在线测试网站：
Bezier Curve Demos
cubic-bezier
贝塞尔曲线在线绘制🚀

PathInterpolator 的构造函数，

PathInterpolator(Path path) ：利用 Path 对象创建插值器。
PathInterpolator(float controlX, float controlY) ：传入一个控制点坐标（controlX，controlY），构造二维贝塞尔曲线插值器。
PathInterpolator(float controlX1, float controlY1, float controlX2, float controlY2) ：传入两个控制点坐标（controlX1，controlY1 ）、（controlX2, controlY2），构造三维贝塞尔曲线插值器。
PathInterpolator(Context context, AttributeSet attrs) ：通过 AttributeSet 加载插值器。

1. PathInterpolator(Path path)

先看通过 PathInterpolator(Path path) 构建。

1.1 Path

构造函数，直接 new Path 创建即可。

	/*** Create an empty path*/public Path() {mNativePath = nInit();sRegistry.registerNativeAllocation(this, mNativePath);}

1.2 Path.moveTo

移动到指定坐标

/*** Set the beginning of the next contour to the point (x,y).** @param x The x-coordinate of the start of a new contour* @param y The y-coordinate of the start of a new contour*/public void moveTo(float x, float y) {nMoveTo(mNativePath, x, y);}

1.3 Path.lineTo(float x, float y)

从上一个点绘制一条线到给定的点（x,y），显而易见，给的坐标决定了动画效果。

	/*** Add a line from the last point to the specified point (x,y).* If no moveTo() call has been made for this contour, the first point is* automatically set to (0,0).** @param x The x-coordinate of the end of a line* @param y The y-coordinate of the end of a line*/public void lineTo(float x, float y) {isSimplePath = false;nLineTo(mNativePath, x, y);}

走直线

看如下代码，X 轴、Y 轴都移动一段距离，X 轴、Y 轴都用 LinearInterpolator ，

ObjectAnimator animationX = ObjectAnimator.ofFloat(imageViewIcon, "translationX",imageViewIcon.getWidth() * 5);
animationX.setInterpolator(new LinearInterpolator());ObjectAnimator animationY = ObjectAnimator.ofFloat(imageViewIcon, "translationY",imageViewIcon.getWidth() * 5);
animationY.setInterpolator(new LinearInterpolator());AnimatorSet set = new AnimatorSet();
set.playTogether(animationX, animationY);
set.setDuration(5000).start();

动画效果， imageViewIcon 按照对角线移动。
在这里插入图片描述
动画轨迹是起点、终点之间的直线，Path.lineTo 画线正合适，用 PathInterpolator 来实现同样的效果， Go ~

		Path path = new Path();path.moveTo(0f,0f);path.lineTo(0.25f,0.25f);path.lineTo(0.5f,0.5f);path.lineTo(0.75f,0.75f);path.lineTo(1f,1f);PathInterpolator pathInterpolator = new PathInterpolator(path);ObjectAnimator animationX = ObjectAnimator.ofFloat(imageViewIcon, "translationX",imageViewIcon.getWidth() * 5);animationX.setInterpolator(pathInterpolator);ObjectAnimator animationY = ObjectAnimator.ofFloat(imageViewIcon, "translationY",imageViewIcon.getWidth() * 5);animationY.setInterpolator(new LinearInterpolator());AnimatorSet set = new AnimatorSet();set.playTogether(animationX,animationY);set.setDuration(5000).start();

使用也简单，三大步：

创建 Path ，选取了 5 个点（可以更多）来绘制 (0f,0f) 到 (1f,1f) 的曲线（效果是直线，直线 ∈ 曲线）。
通过 Path 创建 PathInterpolator 。
动画指定用创建的 pathInterpolator 。控制变量法，X 轴用新创建的 pathInterpolator ， Y 轴继续用 LinearInterpolator 。

效果，
在这里插入图片描述
肉眼看不出和 LinearInterpolator 的差别。

走折线

走折线就是走多条直接嘛，
例，

		Path path = new Path();path.moveTo(0,0);path.lineTo(322,0);//path.lineTo(322,322);path.lineTo(-322,322);path.lineTo(-322,-322);path.lineTo(322,-322);path.lineTo(322,0);path.lineTo(0,0);ObjectAnimator animationX = ObjectAnimator.ofFloat(imageViewRed, "translationX","translationY", path);animationX.setDuration(8000).start();

图
在这里插入图片描述

1.4 Path.arcTo(float left, float top, float right, float bottom, float startAngle,float sweepAngle, boolean forceMoveTo)

画弧，

通过前4个参数确定矩形，从而得到椭圆圆心，

startAngle 是起始位置相对于圆心的角度，sweepAngle 是相对于圆心需要旋转的角度，两者可以确定起始角度，

有圆心，有角度，弧形不就出来了。

	/*** Append the specified arc to the path as a new contour. If the start of* the path is different from the path's current last point, then an* automatic lineTo() is added to connect the current contour to the* start of the arc. However, if the path is empty, then we call moveTo()* with the first point of the arc.** @param startAngle  Starting angle (in degrees) where the arc begins* @param sweepAngle  Sweep angle (in degrees) measured clockwise, treated*                    mod 360.* @param forceMoveTo If true, always begin a new contour with the arc*/public void arcTo(float left, float top, float right, float bottom, float startAngle,float sweepAngle, boolean forceMoveTo) {isSimplePath = false;nArcTo(mNativePath, left, top, right, bottom, startAngle, sweepAngle, forceMoveTo);}

如下代码，走个半圆的动画，
（icon 宽度和黑色线的位置是计算好距离的）

Path path = new Path();
path.arcTo(-imageViewGreen.getWidth()*4, 0, imageViewGreen.getWidth()*4, imageViewGreen.getWidth()*8, 270f, 180f, true);
ObjectAnimator animator = ObjectAnimator.ofFloat(imageViewIcon, View.X, View.Y, path); // 注释1
animator.setDuration(5000);
animator.start();

看注释1 处，用的是 View.X, View.Y 参数，这个例子下和用 “translationX”, “translationY” 是一样的效果。

运行效果，
在这里插入图片描述

附图说明，
在这里插入图片描述

图解，
解释下 path.arcTo(-imageViewGreen.getWidth()*4, 0, imageViewGreen.getWidth()*4, imageViewGreen.getWidth()*8, 270f, 180f, true); 代码参数，

点 A ：图片原始位置，也是动画开始位置。（注意：动画开始位置可以不是图片原始位置）
绿色箭头 j3 ：动画轨迹，本例是半圆。
点 B ：动画结束位置。
黄色框左上角 P1 ：点 P1 由点A 来确定，以动画开始位置为（0,0），它的坐标是（-imageViewGreen.getWidth()*4, 0）。
黄色框右下角 P2 ：点 P2 由点A 来确定，以动画开始位置为（0,0），
它的坐标是（imageViewGreen.getWidth()*4, imageViewGreen.getWidth()*8）。
蓝色线交汇点 O ：黄色框左上角点 P1 和黄色框右下角点 P2 确定了矩形（本例是正方向，正方形 ∈ 矩形），得到了最大内切红色椭圆（本例是正圆，正圆 ∈ 椭圆），确定了圆心点 O 。这个圆心是弧形的圆心，也就是动画旋转的中心。
动画坐标系：以点 O 为圆心得到了动画坐标系，点O 的右方向是 0° ，下方向是 90° 。
按照 j1 旋转为正角度，顺时针旋转为正角度，逆时针旋转为负角度。
startAngle 是 A 点对于圆心O来说需要转 270° ，本例就是 270f 。
sweepAngle 是需要旋转的角度，按照 j1 旋转为正角度，本例是 180f ，即顺时针旋转 180° 。

很绕，捋一捋。如果错误，也请指正。

1.5 Path.arcTo(RectF oval, float startAngle, float sweepAngle)

arcTo 方法的重载，通过 android.graphics.RectF 画弧。

RectF 的构造函数如下，也是通过给定的四个点来确定矩形，然后画弧。

	/*** Create a new rectangle with the specified coordinates. Note: no range* checking is performed, so the caller must ensure that left <= right and* top <= bottom.** @param left   The X coordinate of the left side of the rectangle* @param top    The Y coordinate of the top of the rectangle* @param right  The X coordinate of the right side of the rectangle* @param bottom The Y coordinate of the bottom of the rectangle*/public RectF(float left, float top, float right, float bottom) {this.left = left;this.top = top;this.right = right;this.bottom = bottom;}

示例，

Path path = new Path();
path.arcTo(new RectF(-imageViewGreen.getWidth() * 3,0,imageViewGreen.getWidth() * 3,imageViewGreen.getWidth() * 6),270,-359);
ObjectAnimator animator = ObjectAnimator.ofFloat(imageViewGreen, "translationX", "translationY", path);//注释 2
animator.setDuration(5000);
animator.start();

看注释2 处，用的是 “translationX”, “translationY” 参数，这个例子下和用 View.X, View.Y 是不一样的效果。

效果，绿球绕着红球逆时针旋转 359° ，
在这里插入图片描述

相关参数说明和 1.4 章节的一样。

最后一个参数 sweepAngle 有限制，

传 -360 无动画效果，传 -450 实际上是旋转 -90 的效果。
传 360 无动画效果，传 450 实际上是旋转 90 的效果。

就想要无限循环怎么办？na~ ： animator.setRepeatCount(ValueAnimator.INFINITE);

1.5 Path.quadTo

Path.quadTo ，绘制二阶贝塞尔曲线。起点是 (0,0)，终点是(x2,y2)，控制点是(x1,y1) ，

/*** Add a quadratic bezier from the last point, approaching control point* (x1,y1), and ending at (x2,y2). If no moveTo() call has been made for* this contour, the first point is automatically set to (0,0).** @param x1 The x-coordinate of the control point on a quadratic curve* @param y1 The y-coordinate of the control point on a quadratic curve* @param x2 The x-coordinate of the end point on a quadratic curve* @param y2 The y-coordinate of the end point on a quadratic curve*/public void quadTo(float x1, float y1, float x2, float y2) {isSimplePath = false;nQuadTo(mNativePath, x1, y1, x2, y2);}

例

		Path path = new Path();path.moveTo(0,0);//二阶贝塞尔曲线path.quadTo(400,1300,imageViewGreen.getWidth()*5,imageViewGreen.getWidth()*5);ObjectAnimator animator = ObjectAnimator.ofFloat(imageViewIcon, View.X, View.Y, path);animator.setDuration(5000);animator.start();

图
在这里插入图片描述

1.6 Path.cubicTo

Path.cubicTo，绘制三阶阶贝塞尔曲线，起点是 (0,0)，终点是(x3,y3)，控制点是(x1,y1) 和 (x2,y2) 。

	/*** Add a cubic bezier from the last point, approaching control points* (x1,y1) and (x2,y2), and ending at (x3,y3). If no moveTo() call has been* made for this contour, the first point is automatically set to (0,0).** @param x1 The x-coordinate of the 1st control point on a cubic curve* @param y1 The y-coordinate of the 1st control point on a cubic curve* @param x2 The x-coordinate of the 2nd control point on a cubic curve* @param y2 The y-coordinate of the 2nd control point on a cubic curve* @param x3 The x-coordinate of the end point on a cubic curve* @param y3 The y-coordinate of the end point on a cubic curve*/public void cubicTo(float x1, float y1, float x2, float y2,float x3, float y3) {isSimplePath = false;nCubicTo(mNativePath, x1, y1, x2, y2, x3, y3);}

例

		Path path = new Path();path.moveTo(0,0);path.rCubicTo(1500,100,700,1300,imageViewGreen.getWidth()*5,imageViewGreen.getWidth()*5);ObjectAnimator animator = ObjectAnimator.ofFloat(imageViewIcon, View.X, View.Y, path);animator.setDuration(5000);animator.start();

图
在这里插入图片描述

2. PathInterpolator(float controlX, float controlY)

绘制二阶贝塞尔曲线。起点是 (0,0)，终点是(1,1)，控制点是(controlX, controlY) ，

	/*** Create an interpolator for a quadratic Bezier curve. The end points* <code>(0, 0)</code> and <code>(1, 1)</code> are assumed.** @param controlX The x coordinate of the quadratic Bezier control point.* @param controlY The y coordinate of the quadratic Bezier control point.*/public PathInterpolator(float controlX, float controlY) {initQuad(controlX, controlY);}// ...private void initQuad(float controlX, float controlY) {Path path = new Path();path.moveTo(0, 0);path.quadTo(controlX, controlY, 1f, 1f);initPath(path);}

例，

		PathInterpolator interpolator = new PathInterpolator(0.1f,0.9f);ObjectAnimator animationX = ObjectAnimator.ofFloat(imageViewIcon, "translationX",imageViewIcon.getWidth() * 5);animationX.setInterpolator(interpolator);ObjectAnimator animationY = ObjectAnimator.ofFloat(imageViewIcon, "translationY",imageViewIcon.getWidth() * 5);animationY.setInterpolator(new LinearInterpolator());AnimatorSet set = new AnimatorSet();set.playTogether(animationX,animationY);set.setDuration(5000).start();

图
在这里插入图片描述

3. PathInterpolator(float controlX1, float controlY1, float controlX2, float controlY2)

绘制三阶阶贝塞尔曲线，起点是 (0,0)，终点是(1, 1)，控制点是(controlX1,controlY1) 和 (controlX2,controlY2) 。

	/*** Create an interpolator for a cubic Bezier curve.  The end points* <code>(0, 0)</code> and <code>(1, 1)</code> are assumed.** @param controlX1 The x coordinate of the first control point of the cubic Bezier.* @param controlY1 The y coordinate of the first control point of the cubic Bezier.* @param controlX2 The x coordinate of the second control point of the cubic Bezier.* @param controlY2 The y coordinate of the second control point of the cubic Bezier.*/public PathInterpolator(float controlX1, float controlY1, float controlX2, float controlY2) {initCubic(controlX1, controlY1, controlX2, controlY2);}// ...private void initCubic(float x1, float y1, float x2, float y2) {Path path = new Path();path.moveTo(0, 0);path.cubicTo(x1, y1, x2, y2, 1f, 1f);initPath(path);}

例，

		PathInterpolator interpolator = new PathInterpolator(0, 1f ,1f,0);ObjectAnimator animationX = ObjectAnimator.ofFloat(imageViewIcon, "translationX",imageViewIcon.getWidth() * 5);animationX.setInterpolator(interpolator);ObjectAnimator animationY = ObjectAnimator.ofFloat(imageViewIcon, "translationY",imageViewIcon.getWidth() * 5);animationY.setInterpolator(new LinearInterpolator());AnimatorSet set = new AnimatorSet();set.playTogether(animationX,animationY);set.setDuration(5000).start();

图，
在这里插入图片描述