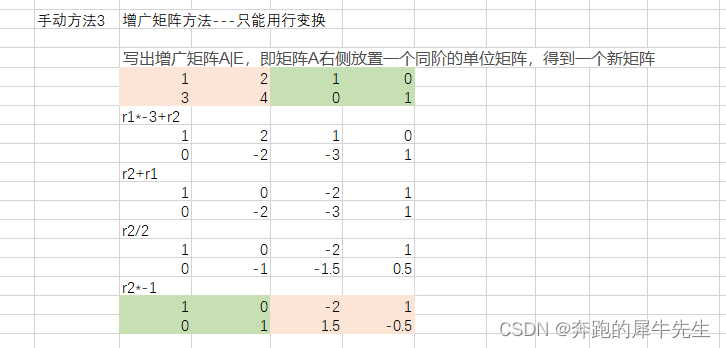
贝叶斯神经网络 - 捕捉现实世界的不确定性 Bayesian Neural Networks 生活本质上是不确定性和概率性的,贝叶斯神经网络 (BNN) 旨在捕获和量化这种不确定性
在许多现实世界的应用中,仅仅做出预测是不够的;您还想知道您对该预测的信心有多大。例如,在医疗保健领域,如果模型表示患者有 70% 的机会患上某种特定疾病,那么其信息量就低于表示患者有 70% 的机会但误差范围为 ±10% 的模型。
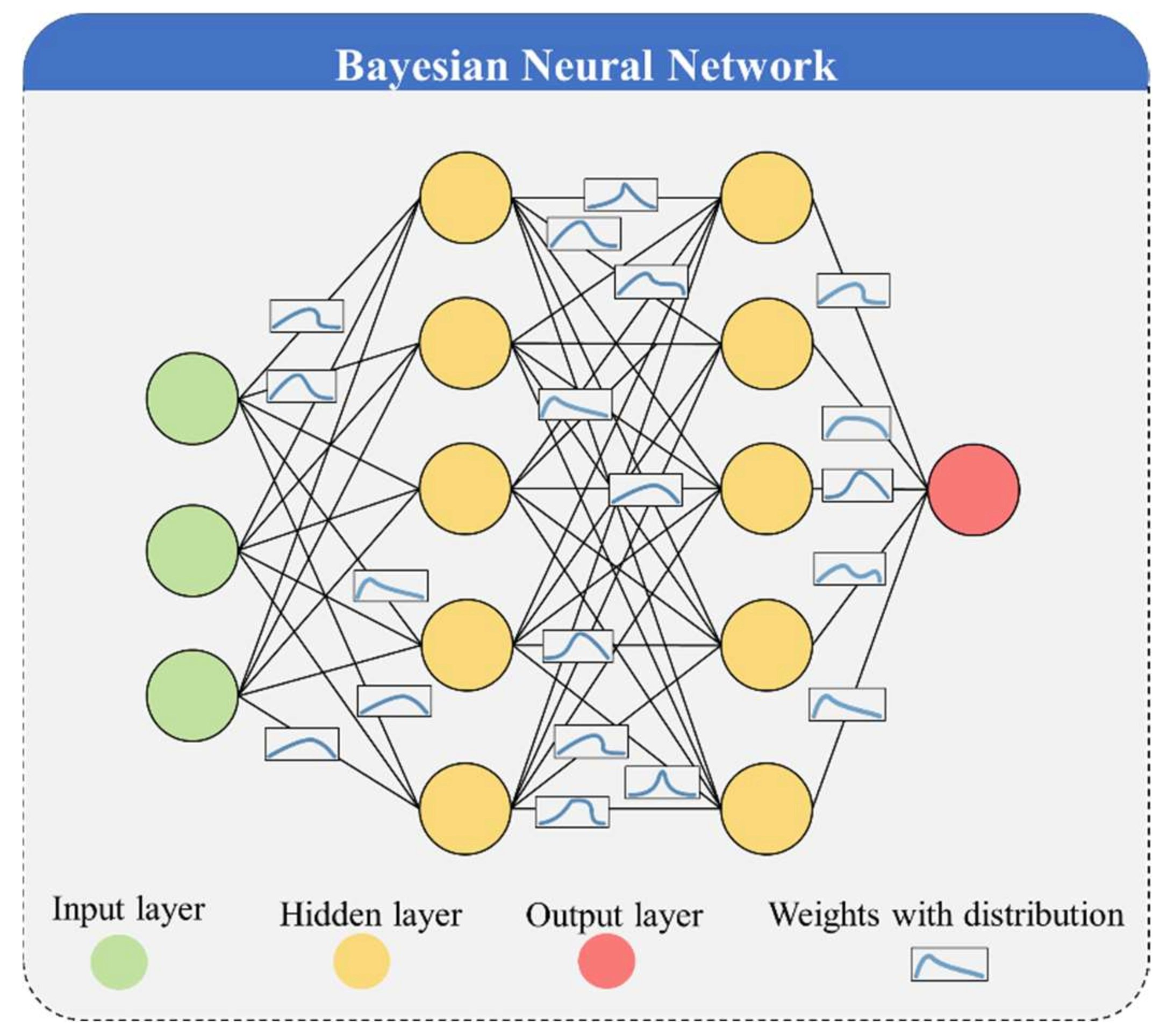
BNN 不太容易过度拟合,可以提高数据效率,因为它们可以合并先验,并且可以输出每个预测的概率分布。了解特定预测准确的不确定性或概率可以建立业务用户的信任和信心。
那么贝叶斯网络是如何工作的呢? 核心思想是用概率分布 P (w) 代替标准神经网络中的固定权重 w
贝叶斯著名的方程是:
P (A| B)= P (B|A) P (A) / P(B)
在 BNN 的背景下:
A 是模型参数(权重和偏差)。 B 是观测数据。 P (A ∣B)是给定数据的参数的后验分布。 P (B ∣ A) 是给定参数的数据的可能性。 P (A) 是参数的先验分布。 P (B)是证据,通常被认为是归一化常数。
先验分布 - 您从权重的先验分布 P (w) 开始。这代表您在看到任何数据之前对模型参数的最初信念。
后验分布 - 目标是计算后验分布 P (w ∣D) ,它表示观察数据 D 后关于权重的更新信念。贝叶斯定理以及一些近似方法用于计算该分布。
预测 - 最后,为了对新输入 x 进行预测,您可以对所有可能的权重进行平均,并按后验概率进行加权:
P (y ∣ x, D)=∫ P (y ∣ x,w)×P (w ∣D) dw
这不仅为您提供了点估计,还为您提供了可能输出 y 的分布,从而捕获了模型的不确定性。
例如:BNN 可以应用于 MRI 扫描数据集,其中每次扫描都标记为“癌症”或“无癌症”。目标是建立一个模型,可以预测新的、未标记的 MRI 扫描的这些标签。 BNN 可以说,“我 80% 确定这是癌症,但有 20% 的可能性不是”,这对临床医生来说是很有价值的信息。
当不确定性量化很重要时,BNN 非常有用,包括疾病诊断、风险评估、能源预测和实时决策
本文由 mdnice 多平台发布