【LeetCode-中等题】208. 实现 Trie (前缀树)

文章目录

- 题目
- 方法一：利用数组构建26叉树
- 方法二：利用哈希表构建26叉树

题目

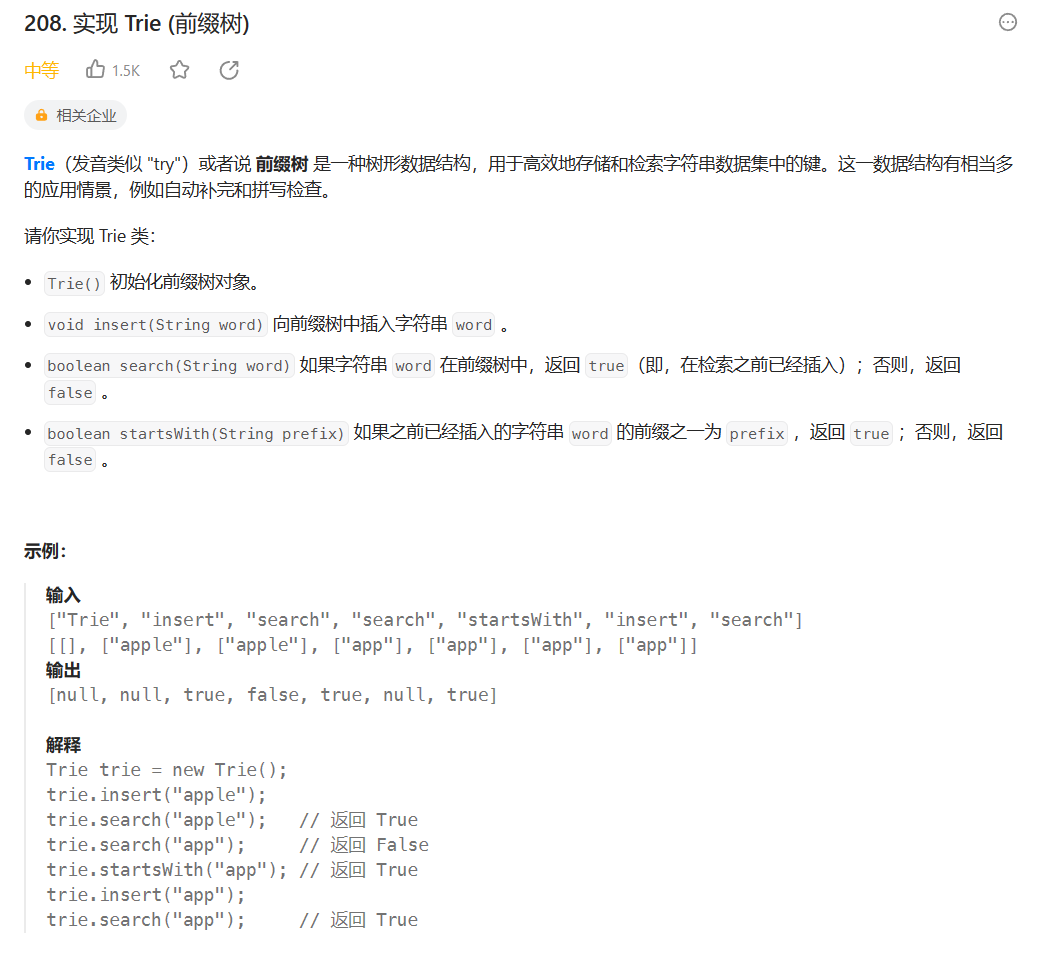
在这里插入图片描述

方法一：利用数组构建26叉树

插入图示：
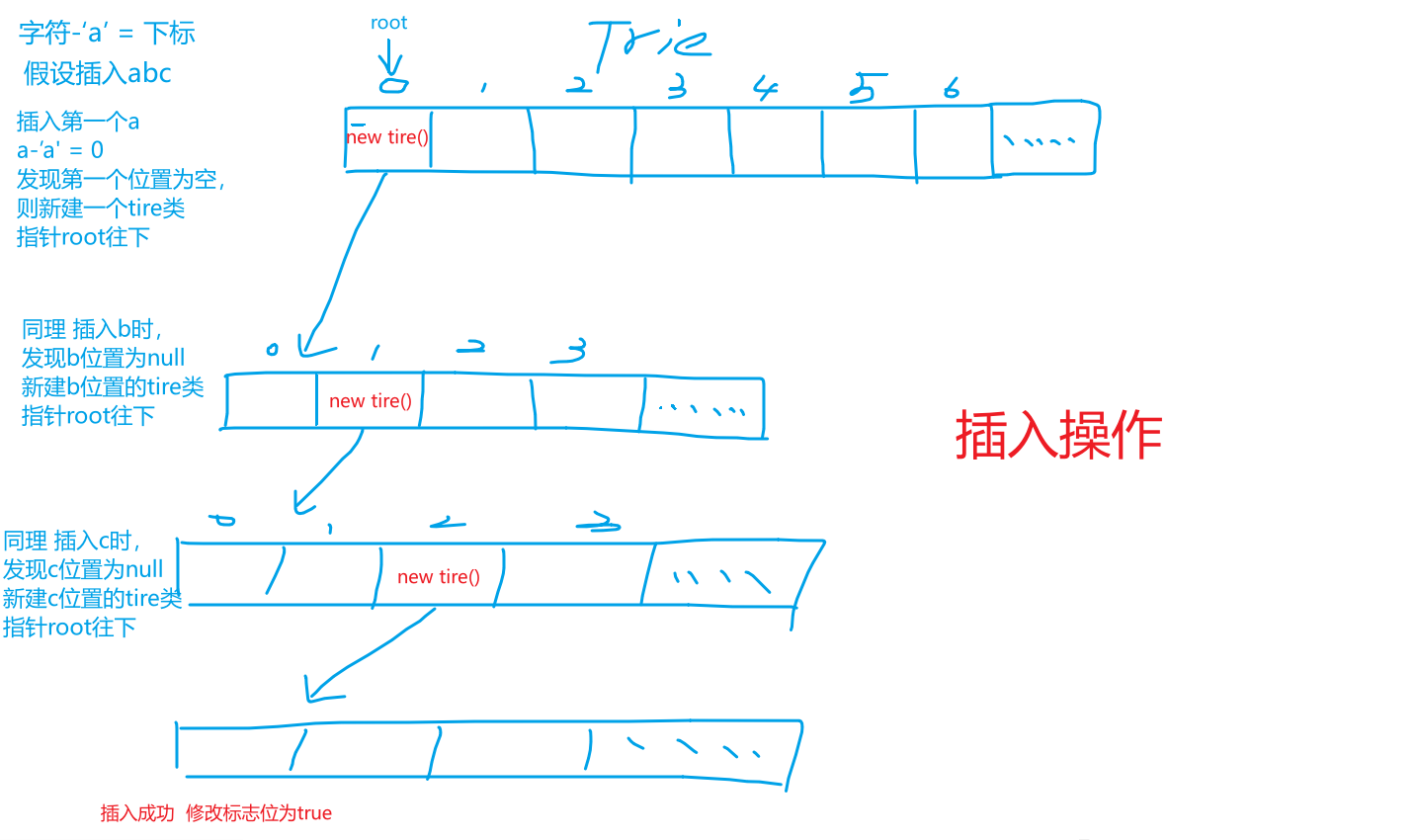
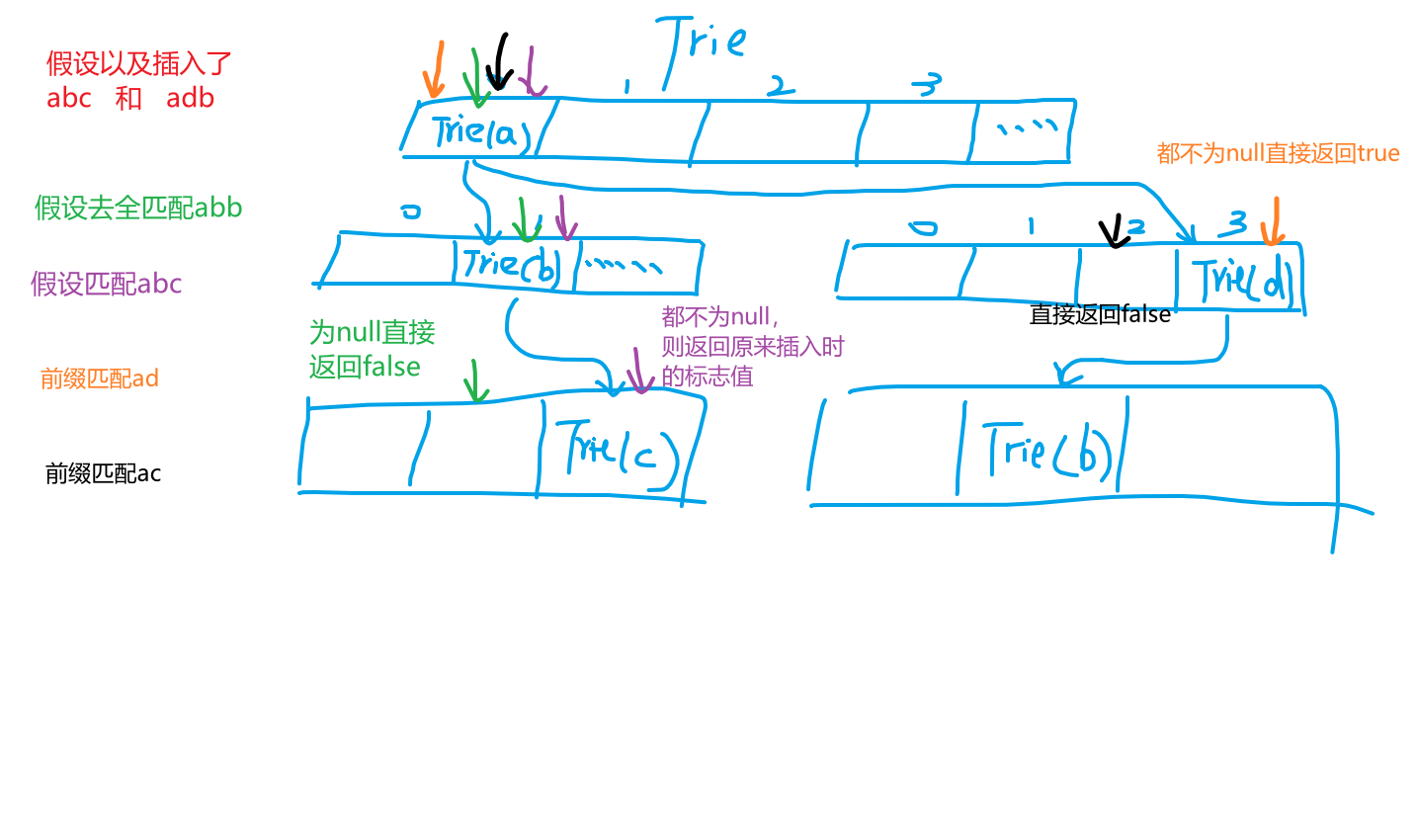
在这里插入图片描述
全搜索和前缀搜索：
注意：全局匹配匹配完直接返回插入时的标志位
而前缀匹配时，匹配成功后直接返回true 因为不需要往下匹配了

匹配到空trie都统统直接返回false
在这里插入图片描述

// 方法一  ： 利用数组存储孩子节点private Trie[] children ; //孩子数组  private boolean isWord ; //标志位public Trie() {//构造函数children = new Trie[26];// 初始化为大小为26的数组isWord = false;//标志位初始化为false}//插入操作public void insert(String word) {Trie root  = this;//给祖先节点赋空对象//此时 孩子数组为空  标志位默认falsefor(int i = 0 ; i<word.length() ; i++){//一个一个拆分字符串，将字符 - 'a' 转换为坐标char ch = word.charAt(i);int idx = ch - 'a';if(root.children[idx] == null){  //如果发现当前位置 为null  则是第一次插入，创建新的trieroot.children[idx] = new Trie();}root = root.children[idx]; //如果当前位置存在，那么将指针指向下一层}root.isWord = true;  //插入完成  标记为true}//全匹配操作public boolean search(String word) {Trie root  = this;//获得当前对象for(int i = 0 ; i<word.length() ; i++){//一个一个拆分字符串，将字符 - 'a' 转换为坐标char ch = word.charAt(i);int idx = ch - 'a';if(root.children[idx] == null){  //如果发现当前位置 为null  说明搜索不到  直接return faslereturn false;}root = root.children[idx]; //如果当前位置存在，那么将指针指向下一层继续搜索}return root.isWord;//如果能搜索到 则直接就是返回本来的状态值}// 前缀匹配public boolean startsWith(String prefix) {Trie root  = this;//获得当前对象for(int i = 0 ; i<prefix.length() ; i++){//一个一个拆分字符串，将字符 - 'a' 转换为坐标`在这里插入代码片`char ch = prefix.charAt(i);int idx = ch - 'a';if(root.children[idx] == null){  //如果发现当前位置 为null  说明搜索不到  直接return faslereturn false;}root = root.children[idx]; //如果当前位置存在，那么将指针指向下一层继续搜索}return true;//如果能搜索到 则直接就是返回true}

方法二：利用哈希表构建26叉树

相比较上面的用数组构建26叉树，其实也可以采用哈希表存储子节点

在这里插入图片描述

方法二  ： 利用hashmap存储孩子节点private Map<Character,Trie> children ; //孩子哈希表  key 为父节点  value为子trie节点  private boolean isWord ; //标志位public Trie() {//构造函数children = new HashMap<>();// 初始化哈希表isWord = false;//标志位初始化为false}//插入操作public void insert(String word) {Trie root  = this;//给祖先节点赋空对象for(int i = 0 ; i<word.length() ; i++){//一个一个拆分字符串，将字符 - 'a' 转换为坐标char ch = word.charAt(i);Trie node = root.children.get(ch);if(node == null){  //如果发现当前位置 为null  则是第一次插入，创建新的trieroot.children.put(ch,new Trie());}root = root.children.get(ch); //如果当前位置存在，那么将指针指向下一层}root.isWord = true;  //插入完成  标记为true}//全匹配操作public boolean search(String word) {Trie root  = this;//获得当前对象for(int i = 0 ; i<word.length() ; i++){//一个一个拆分字符串，将字符 - 'a' 转换为坐标char ch = word.charAt(i);Trie node = root.children.get(ch);if(node == null){  //如果发现当前位置 为null  说明搜索不到  直接return faslereturn false;}root = root.children.get(ch); //如果当前位置存在，那么将指针指向下一层继续搜索}return root.isWord;//如果能搜索到 则直接就是返回本来的状态值}// 前缀匹配public boolean startsWith(String prefix) {Trie root  = this;//获得当前对象for(int i = 0 ; i<prefix.length() ; i++){//一个一个拆分字符串，将字符 - 'a' 转换为坐标char ch = prefix.charAt(i);Trie node = root.children.get(ch);if(node == null){  //如果发现当前位置 为null  说明搜索不到  直接return faslereturn false;}root = root.children.get(ch); //如果当前位置存在，那么将指针指向下一层继续搜索}return true;//如果能搜索到 则直接就是返回true}