2023年数维杯数学建模A题河流-地下水系统水体污染研求解全过程文档及程序

2023年数维杯数学建模

A题河流-地下水系统水体污染研

原题再现：

河流对地下水有着直接地影响，当河流补给地下水时，河流一旦被污染，容易导致地下水以及紧依河流分布的傍河水源地将受到不同程度的污染，这将严重影响工农业的正常运作、社会经济的发展和饮水安全。在地下水污染中最难治理和危害最大的是有机污染，因而对有机污染物在河流-地下水系统中的行为特征进行研究具有十分重要的理论意义和实际价值。另外，已有研究表明在河流地下水系统中有机污染物的行为特征主要涉及对流迁移、水动力弥散、吸附及阻滞等物理过程、化学反应过程以及生物转化过程等。现设地下水渗流场为各向同性均质的稳态流，对有机污染物的迁移和转化规律进行研究和探索，并完成以下问题。
问题1 通过查阅相关文献和资料，分析并建立河流-地下水系统中有机污染物的对流、弥散及吸附作用的数学模型。
问题2 试利用下面介绍的内容和表中试验参数以及数据依据数学模型研究某有机污染物在河流-地下水系统中的迁移转化机理。
1) 对流、弥散试验参数
通过试验测得河流-地下水系统中某有机污染物的对流、弥散有关参数见表1。
在这里插入图片描述
2)吸附动力学试验结果
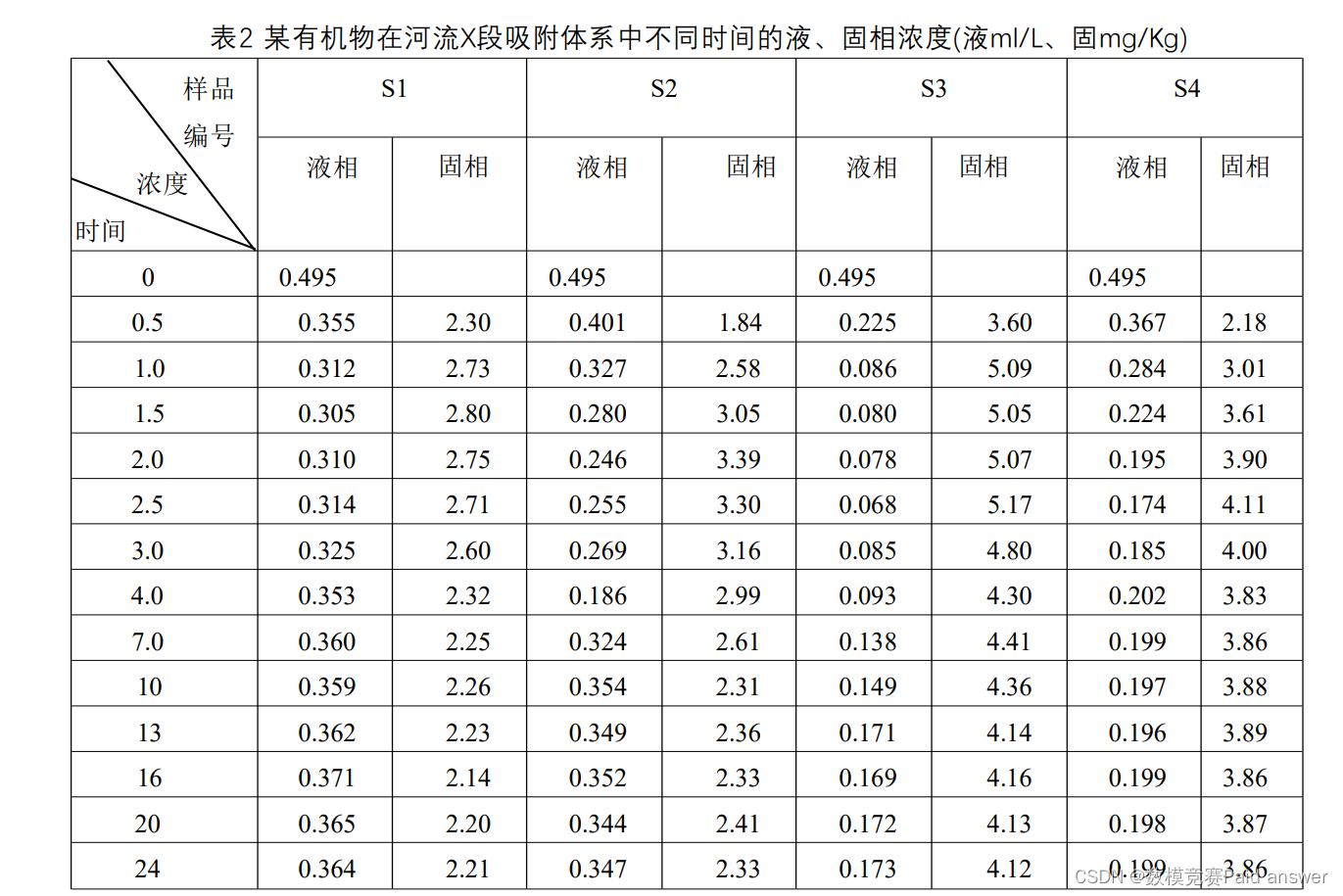
四种不同河流沉积物对初始浓度为0.5mg/L左右的某有机污染物吸附体系的吸附动力学过程及不同吸附时间测得固、液相某有机物的浓度列于表2中.

在这里插入图片描述
3)等温平衡吸附试验结果
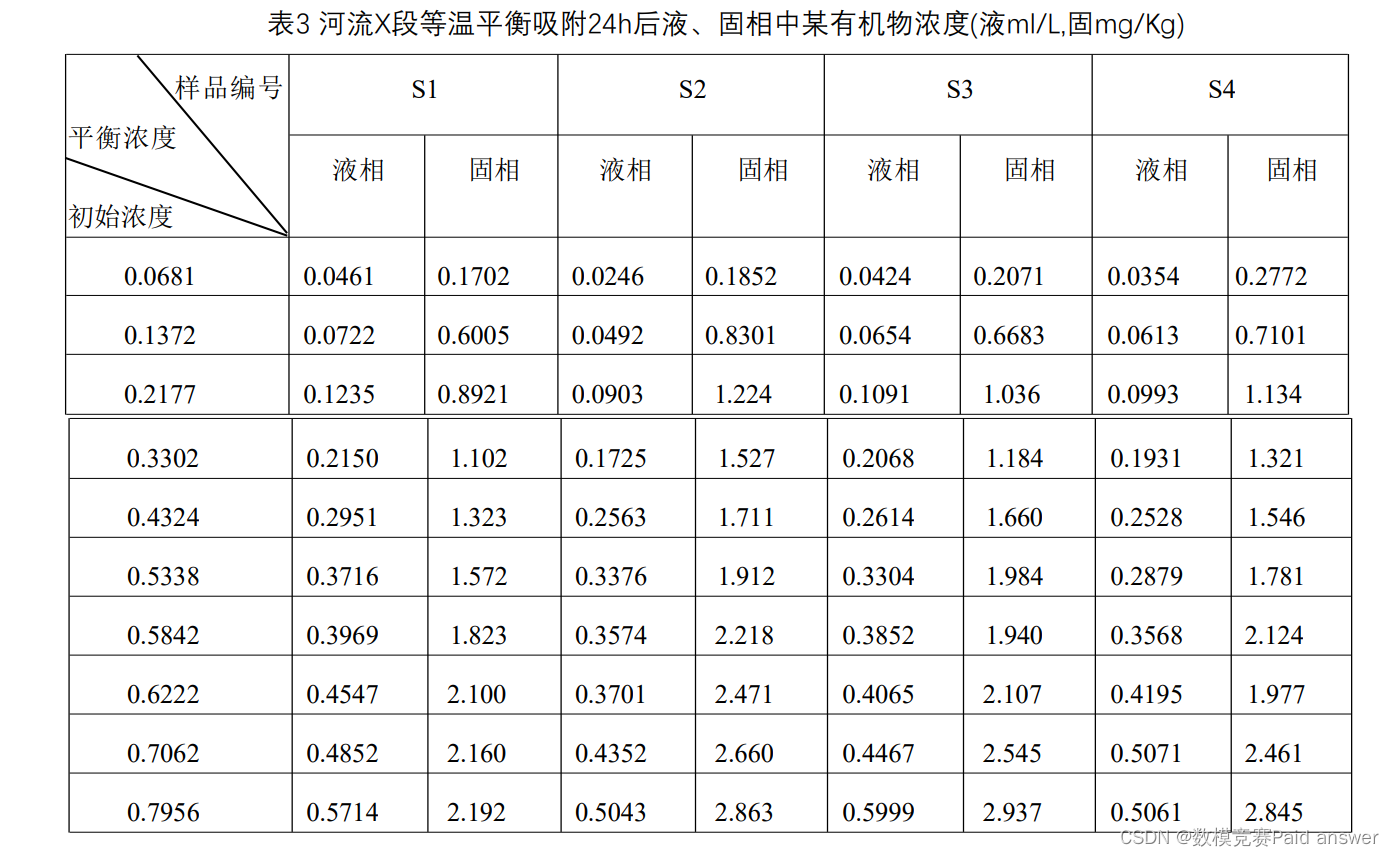
地下水中有机污染物的吸附行为采用等温平衡吸附的数学模型描述，四种不同沉积物对10种不同初始浓度的某有机污染物24小时的等温平衡吸附试验结果列于表3中.

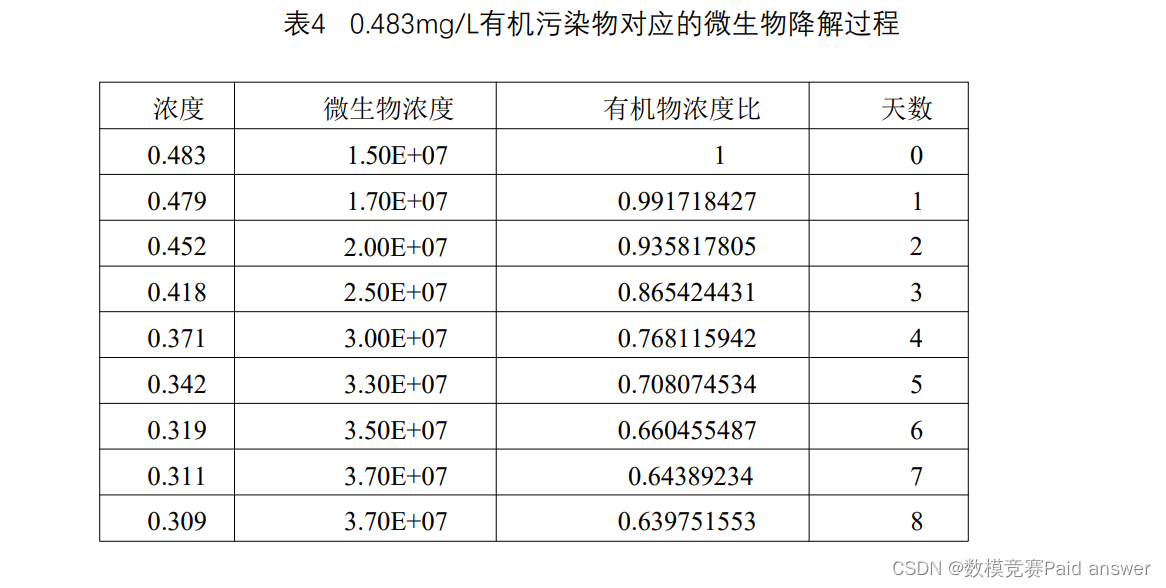
问题3 生物降解是污染物一个很重要的转化过程，考虑生物降解作用对有机污染物转化的影响，建立适当的数学模型，试结合表4中的试验数据分析微生物对该有机污染物的降解特性。
在这里插入图片描述

整体求解过程概述(摘要)

党的二十大报告指出，“深入推进环境污染防治，统筹水资源、水环境、水生态治理，推动重要江河湖库生态保护治理，基本消除城市黑臭水体”。其中河流和地下水系统在人类生活中发挥关键作用。当污染发生时，河流对地下水的补给可能导致周边水源受污，影响工农业运作、社会发展及饮水安全。在地下水污染中，有机污染物的问题最为棘手。为了解这类污染物在河流-地下水系统中的行为，我们需要深入研究其物理、化学反应和生物转化过程。本研究将以各向同性均质的稳态流作为地下水渗流场，探究有机污染物的迁移与转化规律。
对于问题一，我们查阅相关文献资料分别得出对流方程、弥散方程以及吸附作用方程。我们将基于质量守恒方程与一些假设条件，建立描述有机污染物浓度变化的一维及多维对流-弥散-吸附微分方程，接着通过有限差分法求解该一维微分方程，以便直观地观察模型参数对有机污染物迁移转化过程的影响。
对于问题二，我们将基于给定的四种有机物液、固相实验数据，对模型进行参数调整和检验。首先，基于对流、弥散试验参数，更新微分方程的模型参数，以更准确地描述有机污染物的迁移转化过程；然后，根据四种不同河流沉积物的吸附动力学数据，重新计算吸附系数k值，由于给定的时间数据比较离散，本文使用插值方法进行数值模拟，将更新后的k值用于微分方程求解;最后，基于四种有机物液、固相状态下的初始浓度与平衡浓度数据，通过匹配对可以迭代计算出初始浓度与等温吸附24小时后平衡的浓度的吸附系数k值。然后求均值作为吸附系数k，更新微分方程模型参数。
对于问题三，我们将在微分方程模型中引入生物降解过程，以研究微生物对有机污染物的降解特性，假设生物降解速率与微生物浓度M和有机物浓度C之间存在线性关系，则可在原有的对流弥散-吸附模型中添加生物降解项，形成新的数学模型一对流-弥散-吸附-生物降解的微分方程。

问题分析：

问题1要求我们从已有的相关理论研究和实证分析中找到适用于本题的数学模型，用以描述河流-地下水系统中有机污染物的对流、弥散及吸附作用。由于团队相关专业知识的了解程度较低，我们决定将问题简化，建立描述河流-地下水系统中有机污染物变化的一维对流—弥散—吸附微分方程，并通过有限差分法求解该方程，以便能够直观地呈现出模型参数对有机物污染物迁移转化过程的影响，同时有利于求解问题2。
对于第二个问题，我们将基于给定的实验数据，对模型进行参数调整和验证。首先，我们将优化微分方程的模型参数，以更准确地描述有机污染物的迁移转化过程。然后，我们将根据四种不同河流沉淀物的吸附动力学数据，重新计算吸附系数k 值。由于给定的时间数据比较离散，我们将考虑结合插值方法进行数值模拟，最后，我们将对每种有机物在不同状态下的浓度变化情况进行模拟，以验证我们的模型和参数调整的有效性。
对于第三个问题，我们将在微分方程模型中引入生物降解过程，以研究微生物对有机污染物的降解特性。具体地，我们将在原有的对流-弥散-吸附模型中添加生物降解项，形成新的数学模型。然后，我们将根据河流等温平衡吸附24小时后的浓度变化数据，通过迭代计算方法求解吸附系数k值。最后，我们将求得的k值的均值作为新模型的吸附系数k，以此来更新我们的数学模型。

模型假设：

1．一维空间假设:将河流-地下水系统近似为一维空间，忽略横向扩散和纵向非均匀性；
2．连续性假设:假设有机污染物的浓度分布在空间上具有一定的连续性和平滑性，可以用微分方程来描述；
3．线性生物降解假设:假设生物降解速率与微生物浓度和有机物浓度之间存在线性关系，用生物降解速率常数上表示；
4．稳态吸附假设:假设吸附过程处于稳态，吸附系数k不随时间变化；
5．地下水流速相对于孔隙流速u来说较小，因此可以忽略其对流的影响。

论文缩略图：

在这里插入图片描述

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"]
plt.rcParams["axes.unicode_minus"]=False
for dd in range(1,13,3):
# 模型参数
L = 100 # 系统长度（单位：m）
Nx = 24 # 空间离散化点数
T = 24 # 模拟时间（单位：天）
Nt = 1000 # 时间离散化步数
dx = L / (Nx - 1) # 空间步长
dt = T / Nt # 时间步长
v = 0.1 # 水流速度（单位：m/day）
D = 0.01 # 弥散系数（单位：m²/day）
k = 0.001 # 吸附系数（单位：1/day）
# 初始条件
C0 = np.zeros(Nx) # 初始浓度分布
C0[int(Nx / 2)] =dd # 在中心位置设置初始浓度为1.0
# 数值求解
C = np.zeros((Nt, Nx)) # 存储浓度分布的数组
C[0, :] = C0
for t in range(1, Nt)
for x in range(1, Nx - 1):
# 对流项
convective = -v * (C[t-1, x] - C[t-1, x-1]) / dx
# 弥散项
dispersive = D * (C[t-1, x+1] - 2 * C[t-1, x] + C[t-1, x-1]) / (dx**2)
# 吸附项
adsorption = -k * C[t-1, x]
# 数值更新
C[t, x] = C[t-1, x] + dt * (convective + dispersive + adsorption)
# 绘制浓度随时间和空间的分布图
x = np.linspace(0, L, Nx)
t = np.linspace(0, T, Nt)
X, T = np.meshgrid(x, t)
plt.contourf(X, T, C, cmap='cool')
plt.colorbar(label='浓度')
plt.xlabel('距离 (m)')
plt.ylabel('天数 (days)')
plt.title('浓度为%s_污染物浓度'%dd)
plt.savefig('./Q1/浓度为%s_污染物浓度.jpg'%dd)
plt.show()

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"]
plt.rcParams["axes.unicode_minus"]=False
for dd in range(1,13,3):
# 模型参数
L = 100 # 系统长度（单位：m）
Nx = 24 # 空间离散化点数
T = 24 # 模拟时间（单位：天）
Nt = 1000 
dx = L / (Nx - 1) # 空间步长
dt = T / Nt # 时间步长
v = 0.1 # 水流速度（单位：m/day）
D = 0.01 # 弥散系数（单位：m²/day）
k = 0.001 # 吸附系数（单位：1/day）
# 初始条件
C0 = np.zeros(Nx) # 初始浓度分布
C0[int(Nx / 2)] =dd # 在中心位置设置初始浓度为1.0
# 数值求解
C = np.zeros((Nt, Nx)) # 存储浓度分布的数组
C[0, :] = C0
for t in range(1, Nt):
for x in range(1, Nx - 1):
# 对流项
convective = -v * (C[t-1, x] - C[t-1, x-1]) / dx
# 弥散项
dispersive = D * (C[t-1, x+1] - 2 * C[t-1, x] + C[t-1, x-1]) / (dx**2)
# 吸附项
adsorption = -k * C[t-1, x]
# 数值更新
C[t, x] = C[t-1, x] + dt * (convective + dispersive + adsorption)
# 绘制浓度随时间和空间的分布图
x = np.linspace(0, L, Nx)
t = np.linspace(0, T, Nt)
X, T = np.meshgrid(x, t)
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, T, C, cmap='viridis')
ax.set_xlabel('距离 (m)')
ax.set_ylabel('天数 (days)')
ax.set_zlabel('浓度')
ax.set_title('浓度为%s_污染物浓度' % dd)
plt.savefig('./Q2_1/_浓度为%s_污染物浓度.jpg' % dd)
plt.show()

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
plt.rcParams['font.sans-serif'] = ['STSong']
plt.rcParams['axes.unicode_minus'] = False
# 创建数据集
data3 = pd.DataFrame({
'初始浓度': [0.0681, 0.1372, 0.2177, 0.3302, 0.4324, 0.5338, 0.5842, 0.6222, 0.7062, 0.7956],
'S1液相': [0.0461, 0.0722, 0.1235, 0.2150, 0.2951, 0.3716, 0.3969, 0.4547, 0.4852, 0.5714],
'S1固相': [0.1702, 0.6005, 0.8921, 1.102, 1.323, 1.572, 1.823, 2.100, 2.160, 2.192],
'S2液相': [0.0246, 0.0492, 0.0903, 0.1725, 0.2563, 0.3376, 0.3574, 0.3701, 0.4352, 0.5043],
'S2固相': [0.1852, 0.8301, 1.224, 1.527, 1.711, 1.912, 2.218, 2.471, 2.660, 2.863],
'S3液相': [0.0424, 0.0654, 0.1091, 0.2068, 0.2614, 0.3304, 0.3852, 0.4065, 0.4467, 0.5999],
'S3固相': [0.2071, 0.6683, 1.036, 1.184, 1.660, 1.984, 1.940, 2.107, 2.545, 2.937],
'S4液相': [0.0354, 0.0613, 0.0993, 0.1931, 0.2528, 0.2879, 0.3568, 0.4195, 0.5071, 0.5061],
'S4固相': [0.2772, 0.7101, 1.134, 1.321, 1.546, 1.781, 2.124, 1.977, 2.461, 2.845]
})
# 创建数据集
data4 = pd.DataFrame({
'浓度': [0.483, 0.479, 0.452, 0.418, 0.371, 0.342, 0.319, 0.311, 0.309],
'微生物浓度': [1.50E+07, 1.70E+07, 2.00E+07, 2.50E+07, 3.00E+07, 3.30E+07, 3.50E+07, 3.70E+07, 3.70E+07],
'有机物浓度比': [1, 0.991718427, 0.935817805, 0.865424431, 0.768115942, 0.708074534, 0.660455487, 0.64389234, 0.639751553],
'天数': [0, 1, 2, 3, 4, 5, 6, 7, 8]
})
from scipy.interpolate import interp1d
for ii in data3.columns[1:]:
# 模型参数
L = 100 # 系统长度（单位：m）
Nx = 24 # 空间离散化点数
T = 24 # 模拟时间（单位：天）
Nt = 1000 # 时间离散化步数
dx = L / (Nx - 1) # 空间步长
dt = T / Nt # 时间步长
# 河流-地下水参数
u = 38.67 * 0.01 # 平均孔隙流速（单位：m/day），将单位转换为cm/d
ν = 5.01 * 0.01 # 地下水渗流流速（单位：m/day），将单位转换为cm/d
D = 0.38 * (1 / 1440) * 0.01**2 # 弥散系数（单位：cm²/min 转换为 m²/d）
k = 6.32 * 0.01 # 渗透系数（单位：m/day），将单位转换为cm/d
μ = 0.01 # 生物降解速率常数
# 含水层样品的干密度和孔隙度
ρ = 1.67 # 干密度（单位：g/cm³）
n = 0.375 # 孔隙度
print(ii)
temp=data3[['初始浓度',ii]]
k_list=[]
for i in range(temp.shape[0]):
# 计算吸附系数
C_max =temp.iloc[i,0] # 最大吸附浓度
Ce = temp.iloc[i,1] # 平衡浓度
k = C_max / (Ce - C_max) * (ρ * n)
k_list.append(k)
k=np.mean(k_list)
# 初始条件
C0 = np.zeros(Nx) # 初始浓度分布
C0[int(Nx / 2)] =0.483# 在中心位置设置初始浓度为1.0
# 数值求解
C = np.zeros((Nt, Nx)) # 存储浓度分布的数组
C[0, :] = C0
# 创建插值函数
# 时间插值
interp_func = interp1d(data4['天数'], data4['浓度'], kind='quadratic')
time_interp = np.linspace(0, T, Nt)
for t in range(1, Nt):
for x in range(1, Nx - 1):
# 对流项
convective = -(u + ν) * (C[t-1, x] - C[t-1, x-1]) / dx
# 弥散项
dispersive = D * (C[t-1, x+1] - 2 * C[t-1, x] + C[t-1, x-1]) / (dx**2)
# 吸附项
adsorption = -k * (ρ * n * C[t-1, x])
# 生物降解项
bio_degradation = -μ * C[t-1, x] * interp_func(np.clip([t * dt], 0, data4["浓
度"].iloc[-1]))
# 数值更新
C[t, x] = C[t-1, x] + dt * (convective + dispersive + adsorption +
bio_degradation)
# # 数值更新
# C[t, x] = C[t-1, x] + dt * (convective + dispersive + adsorption)
# 绘制浓度随时间和空间的分布图
x = np.linspace(0, L, Nx)
t = np.linspace(T, 0, Nt)
if '固' in ii:
# 绘制浓度随时间和空间的分布图
x = np.linspace(0, L, Nx)
t = np.linspace(0, T, Nt)
else:
# 绘制浓度随时间和空间的分布图
x = np.linspace(0, L, Nx)
t = np.linspace(T, 0, Nt)
X, T = np.meshgrid(x, t)
plt.contourf(X, T, C, cmap='seismic')
plt.colorbar(label='浓度')
plt.xlabel('距离 (m)')
plt.ylabel('天数 (days)')
plt.title('%s 污染物浓度'%ii)
plt.savefig('./Q3/%s 污染物浓度.jpg'%ii)
plt.show()