阿丹解读：

之前的文章中写道了有关mysql底层索引，那么在数据量特别大的情况下。mysql采用了B+来管理索引。和存储的数据。

Mysql--技术文档--索引-《索引为什么查找数据快？》-超底层详细说明索引_一单成的博客-CSDN博客

B树解读：

Mysql--技术文档--B树-数据结构的认知_一单成的博客-CSDN博客

基本概念-B+树/B树

B树（B-tree）和B+树（B+ tree）是常见的自平衡搜索树数据结构，用于在存储和检索大量数据时提供高效的操作。它们具有一些共同的基本概念：

节点（Node）：B树和B+树的数据存储在节点中。节点可以包含多个关键字和对应的指针。在B树中，叶子节点和内部节点的结构相同，都存储数据和关键字。而在B+树中，叶子节点只存储关键字和指向数据的指针，而内部节点存储关键字和指向子节点的指针。

关键字（Key）：关键字是B树和B+树中用于对数据进行排序和搜索的值。关键字按照升序排列，并被存储在节点中。

指针（Pointer）：指针用于连接节点，形成树的结构。在B树和B+树中，指针可以指向子节点、父节点或兄弟节点，实现树的平衡。

根节点（Root Node）：根节点是B树和B+树的顶层节点。它是树的起点，通过根节点可以访问到整个树的结构。

叶节点（Leaf Node）：叶节点是树的最底层节点。在B树中，叶节点存储数据和关键字。而在B+树中，叶节点只存储关键字和指向数据的指针。叶节点之间通过指针进行连接，形成一个有序的双向链表。

内部节点（Internal Node）：内部节点是B树和B+树中非叶节点。它们用于指向子节点，并存储关键字。

B树和B+树作为自平衡的搜索树，具有增删改查的操作，每次操作后都会进行平衡以保持树的高度接近最小值。这样可以确保查询效率的稳定性，并提供高效的范围查询和区间搜索能力。

以上是B树和B+树的基本概念，它们在实际应用中有着广泛的应用，尤其在数据库和文件系统中用于管理和查找大量数据。

B+树

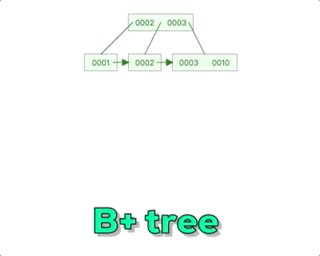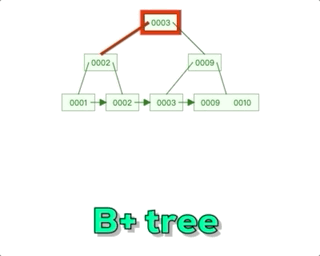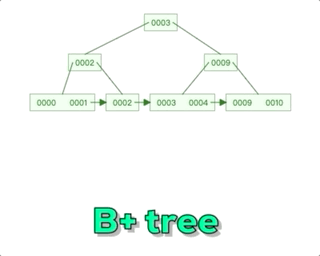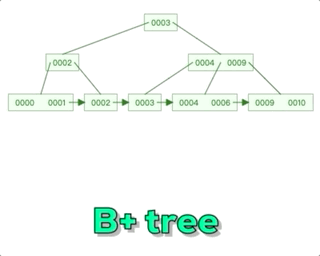
B+树相对于B树主要有一个关键区别，那就是在每个子节点之间添加了指针。在B+树中，所有的数据记录都存储在叶子节点上，而非叶子节点只存储索引信息。每个非叶子节点都有指向其子节点的指针，形成一个链表结构，这个链表结构使得在范围查询时更加高效。而对于B树，非叶子节点既存储索引信息又存储部分数据记录。所以可以说B+树的设计更适合在数据库等需要范围查询的场景中使用。这种设计有效地减少了磁盘I/O操作的次数，提高了查询效率。

当谈到B+树和B树的区别时，以下是一些重要的方面需要考虑：

数据记录存储：在B树中，每个节点都包含索引和对应的数据记录。而在B+树中，只有叶子节点包含数据记录，而非叶子节点只包含索引信息。这使得B+树的叶子节点形成了一个有序链表，便于范围查询操作。
非叶子节点的指针：在B树中，非叶节点包含指向子节点的指针。而在B+树中，非叶子节点只包含指向子节点的指针，并且这些指针形成了一个链表结构。这样的设计可以更快地在范围查询时遍历数据。
查询性能：由于B+树的叶子节点上存储了较多的数据记录，并且有序排列，所以范围查询效率更高。而B树需要在非叶子节点和叶子节点之间来回检索，相对而言，范围查询的性能较差。
插入和删除操作：对于B+树来说，由于只需调整叶子节点的指针，所以插入和删除操作相对较快。而B树在插入和删除时可能需要在非叶子节点之间进行调整。

总体来说，B+树在数据库系统中更为常见，尤其在需要范围查询和排序的场景中非常适用。对于大型数据库，B+树的使用可以提供更高的性能和效率。而B树在一些特殊场景中可能仍然有其应用，但在绝大多数情况下，B+树是更好的选择。

B+树复杂度

B+树的复杂度取决于具体的操作，下面是一些常见操作的复杂度分析：

插入和删除：B+树的插入和删除操作通常具有O(log N)的时间复杂度，其中N是树中的节点数。插入和删除通常需要在树的高度上进行搜索，并且在找到合适的位置后，可能需要进行节点的分裂或合并操作。
查找：B+树的查找操作也具有O(log N)的时间复杂度。通过从根节点开始，根据索引值逐级搜索子节点，直到叶子节点找到目标记录。
范围查询：由于B+树的叶子节点形成有序链表，使得范围查询操作非常高效。通过定位范围的起始和结束位置，可以在O(log N + M)的时间复杂度内定位到范围内的M个记录。

注意：这些复杂度分析是对平衡的B+树而言。在实际使用中，性能可能受到硬件、存储引擎、数据分布和索引设计等多个因素的影响。因此，在特定情况下，可能需要进一步考虑这些因素以获得更准确的性能评估。

提供一个网址可手动看见树的工作流程

B-Tree Visualization

详解工作流程

B+树的根节点是一个特殊的节点，存储在内存中，并且是树的入口点。根节点可以包含一些索引信息，指向下层节点。
当需要插入一条记录时，首先从根节点开始，按照索引值逐级向下搜索，找到合适的叶子节点。在叶子节点中，根据索引值的顺序将记录插入到合适的位置。
如果插入操作导致叶子节点超过了预设的容量，会进行节点的分裂操作。分裂会创建一个新的叶子节点，并将一部分记录移动到新节点中。同时，更新上层节点的索引信息以反映叶子节点的变化。
当需要删除一条记录时，同样从根节点开始搜索，找到包含目标记录的叶子节点，并将其删除。
如果删除操作导致叶子节点的记录数过少，会进行节点的合并操作。合并操作会将相邻的叶子节点合并为一个节点，并更新上层节点的索引信息。
在B+树中进行范围查询时，首先定位到起始位置和结束位置所在的叶子节点，然后按照链表结构遍历那些在范围内的叶子节点，找到满足条件的记录。

总之，B+树的工作流程是从根节点开始，按索引值逐级搜索，最终找到叶子节点来插入、删除或查询记录。在修改树的结构时，可能需要进行节点的分裂和合并操作，以保持树的平衡性。这种工作流程使得B+树在数据库中成为一种高效的索引结构，适用于大规模数据存储和高性能查询的场景。

相对于B树的升级点以及特性点

范围查询效率更高：B+树的叶子节点形成有序链表，使得范围查询操作更高效。通过链表结构，可以轻松地在范围内遍历叶子节点，从而实现更快速的范围查询。
只有叶子节点存储数据记录：在B+树中，只有叶子节点存储数据记录，而非叶子节点只存储索引信息。这种设计减少了冗余数据的存储，提高了数据存储的效率。
非叶子节点的指针：B+树的非叶子节点包含指向子节点的指针，并形成链表结构。这样的设计使得范围查询更高效，因为只需要在链表上遍历节点，而不需要返回到父节点进行下一步搜索。
插入和删除操作更高效：插入和删除操作只需要在叶子节点上进行操作，而不需要涉及到上层非叶子节点。这样可以减少操作的复杂性和开销，提高了插入和删除操作的效率。
有利于磁盘I/O的优化：B+树的有序链表结构有利于优化磁盘I/O操作。通过顺序读取叶子节点的数据记录，可以减少随机I/O的次数，提高磁盘访问的效率。
适用于大型数据库系统：由于B+树的优化特性，它更适用于大型数据库系统。B+树在处理大量数据和频繁查询时表现良好，具有更好的查询性能和数据存储效率。

总体而言，B+树相对于B树提供了更高效的范围查询、更高的插入和删除效率以及更好的存储效率。这使得B+树成为了许多数据库系统中常用的索引结构。

mysql中的B+树

在MySQL中，B+树被广泛应用于索引结构。B+树在数据库系统中解决了多个问题，并且成为了一种优秀的索引方案，这也是为什么它被使用的原因之一。

以下是MySQL中B+树的应用和解决的问题：

高效数据访问：B+树的有序链表结构和索引在叶子节点的使用，使得在数据库中高效地访问和查询数据成为可能。通过树的平衡和有序性，B+树的查询操作可以在最坏情况下以O(log N)的时间复杂度完成，这意味着即使对于大量数据，查询也可以很快完成。
范围查询优化：B+树的特性之一是叶子节点形成有序链表，这使得范围查询的执行非常高效。例如，对于给定的范围条件，可以直接定位到范围内的第一个叶子节点，并沿着链表顺序遍历到最后一个满足条件的叶子节点，从而减少了搜索的次数。
数据排序：B+树可以根据索引的有序性来对数据进行排序。当表使用B+树作为主键索引时，在插入新记录或更新现有记录时，B+树会自动维护有序性。
减少磁盘访问：B+树的有序链表结构和索引的使用有助于优化磁盘I/O操作。通过顺序读取叶子节点，可以减少磁盘随机I/O的次数，从而提高了查询性能。
支持快速插入和删除：B+树的插入和删除操作通常只需要操作叶子节点，不涉及上层非叶子节点。这减少了操作的复杂性和开销，提高了插入和删除操作的效率。

总的来说，MySQL中的B+树应用广泛，它解决了高效数据访问、范围查询优化、数据排序和减少磁盘访问等问题。使用B+树作为索引结构可以提供更好的查询性能、支持大型数据库系统，并且具备高效的数据插入和删除操作。