文章目录
- Acwing:前缀和示例
- 2845.统计趣味子数组的数目
- 思路
- 容易理解的写法:前缀和+两层循环
- 存在问题:超时
- 优化写法:两数之和思路,转换为哈希表
前缀和,就是求数组中某一段的所有元素的和。
求子数组中某一段数字的元素和,只需要转换成两个数字的差值就可以了。
注意:
- 只能求连续某一段区间的元素和
- 一般来说前缀和需要在前面加一个0,因为表示成两个数字的差的话,如果前面不加0,带有第一个数字的元素和无法表示成差值,例如下图

Acwing:前缀和示例
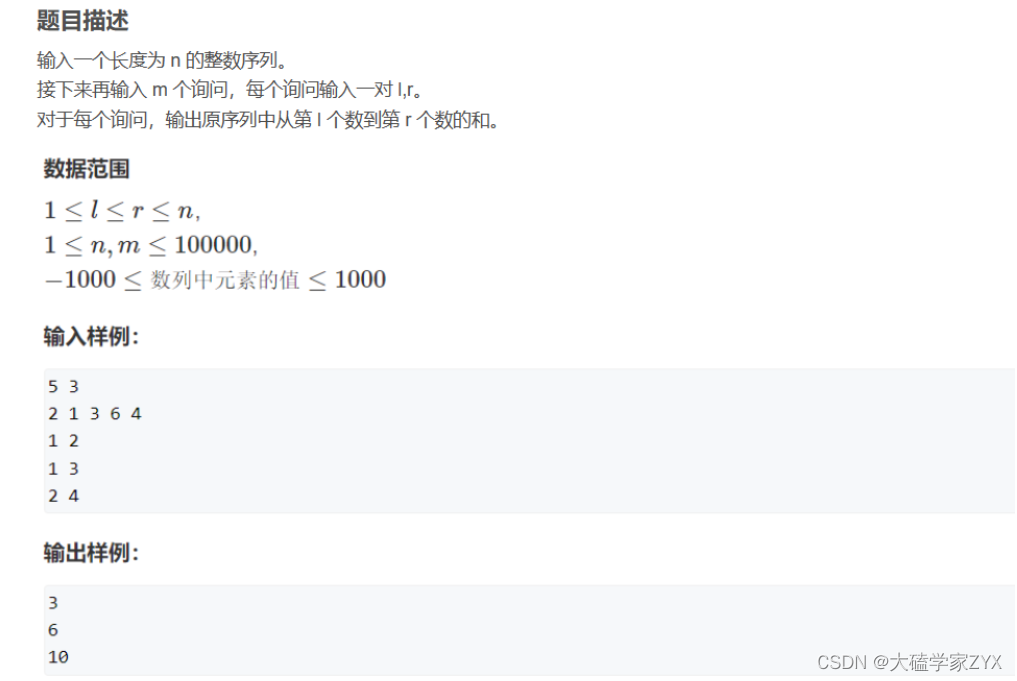
- 前缀和注意:需要在最前面加上一个0,所以前缀和数组大小是nums.size()+1
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int main()
{int n, m, l, r;scanf("%d%d", &n, &m);int a[n], sum[n + 1]; // s设置为n+1是为了后面计算方便for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);sum[0] = 0;for (int i = 0; i < n; i ++ ) sum[i + 1] = sum[i] + a[i];while (m -- ) {scanf("%d%d", &l, &r);printf("%d\n", sum[r] - sum[l - 1]); // 这里的l和r是1~n范围}return 0;
}- 读入两个整数
n和m。n是数组a的大小,m是查询的数量。 - 定义数组
a和sum。a用于存储输入的整数序列,sum用于存储前缀和。 - 初始化
sum[0]为0。 - 使用循环计算
sum数组,其中sum[i]存储了数组a的前i个元素的和。 - 循环进行
m次查询,每次查询读入两个整数l和r,然后输出区间[l, r]的和。这个和可以通过sum[r] - sum[l - 1]很快得到。注意,这里的l和r是1-based,也就是从1开始的,而数组索引是0-based。所以可以直接用sum[r]-sum[l-1],因为r本身已经是对应的下标+1了。
代码示例中的 sum[r] - sum[l - 1] 是核心点。为了理解它,考虑下面的例子:
a: 2 3 4 5
sum: 0 2 5 9 14
为了得到 [2, 4] (这里的下标r和l是从1开始的)子区间和 (即 3 + 4 + 5),我们可以使用 sum[4] - sum[2 - 1],结果为 12。
2845.统计趣味子数组的数目
给你一个下标从 0 开始的整数数组 nums ,以及整数 modulo 和整数 k 。
请你找出并统计数组中 趣味子数组 的数目。
如果 子数组 nums[l..r] 满足下述条件,则称其为 趣味子数组 :
- 在范围
[l, r]内,设cnt为满足nums[i] % modulo == k的索引i的数量。并且cnt % modulo == k。
以整数形式表示并返回趣味子数组的数目。
**注意:**子数组是数组中的一个连续非空的元素序列。
示例 1:
输入:nums = [3,2,4], modulo = 2, k = 1
输出:3
解释:在这个示例中,趣味子数组分别是:
子数组 nums[0..0] ,也就是 [3] 。
- 在范围 [0, 0] 内,只存在 1 个下标 i = 0 满足 nums[i] % modulo == k 。
- 因此 cnt = 1 ,且 cnt % modulo == k 。
子数组 nums[0..1] ,也就是 [3,2] 。
- 在范围 [0, 1] 内,只存在 1 个下标 i = 0 满足 nums[i] % modulo == k 。
- 因此 cnt = 1 ,且 cnt % modulo == k 。
子数组 nums[0..2] ,也就是 [3,2,4] 。
- 在范围 [0, 2] 内,只存在 1 个下标 i = 0 满足 nums[i] % modulo == k 。
- 因此 cnt = 1 ,且 cnt % modulo == k 。
可以证明不存在其他趣味子数组。因此,答案为 3 。
示例 2:
输入:nums = [3,1,9,6], modulo = 3, k = 0
输出:2
解释:在这个示例中,趣味子数组分别是:
子数组 nums[0..3] ,也就是 [3,1,9,6] 。
- 在范围 [0, 3] 内,只存在 3 个下标 i = 0, 2, 3 满足 nums[i] % modulo == k 。
- 因此 cnt = 3 ,且 cnt % modulo == k 。
子数组 nums[1..1] ,也就是 [1] 。
- 在范围 [1, 1] 内,不存在下标满足 nums[i] % modulo == k 。
- 因此 cnt = 0 ,且 cnt % modulo == k 。
可以证明不存在其他趣味子数组,因此答案为 2 。
提示:
1 <= nums.length <= 10^51 <= nums[i] <= 10^91 <= modulo <= 10^90 <= k < modulo
思路
首先思路就是运用前缀和,单独开一个x数组遍历所有的nums[i],满足条件计数为1,不满足条件计数为0。
这样的话,子数组[l,r]内满足条件的数字个数,直接就是子数组对应的x数组区间的和!
容易理解的写法:前缀和+两层循环
#include <vector>class Solution {
public:long countInterestingSubarrays(std::vector<int>& nums, int modulo, int k) {int n = nums.size();// 创建一个数组x来标记哪些数字模`modulo`后等于kstd::vector<int> x(n, 0);// 创建一个前缀和数组std::vector<int> sum(n + 1, 0);// ----------- 前缀和计算开始 -----------for (int i = 0; i < n; ++i) {// 如果当前数字模`modulo`后等于k,则在x数组中的对应位置标记为1if (nums[i] % modulo == k) x[i] = 1;// 计算前缀和:当前位置的前缀和等于上一个位置的前缀和加上x数组中的当前值sum[i + 1] = sum[i] + x[i];}// ----------- 前缀和计算结束 -----------// 初始化答案为0long ans = 0;// 使用两重循环来检查所有可能的子数组和for (int l = 0; l < n; ++l) { // 子数组的开始位置for (int r = l + 1; r <= n; ++r) { // 子数组的结束位置// 如果子数组的和模`modulo`后等于k,则增加答案的值if ((sum[r] - sum[l]) % modulo == k) ans++;}}// 返回答案return ans;}
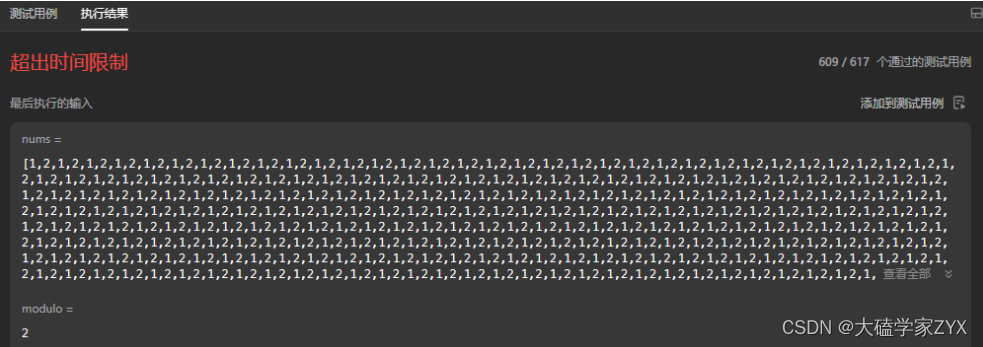
};存在问题:超时
这种写法因为子数组两边都不定,会超时,时间复杂度是O(n^2)。
优化写法:两数之和思路,转换为哈希表
因为上面写法出现了超时,我们可以用类似 两数之和 的套路,来优化时间复杂度,用map来减少一层循环。
-
两数之和的优化方法是,遍历到nums[i]的时候,先看看target-nums[i]是不是已经在map里面了。如果在直接返回,不在就加到map里面,继续遍历数字。遍历完了数组之后一定会收集所有的相加=目标和的两数组合。
-
本题的优化方法是,我们遍历sum[r]的时候,找满足sum[r] - sum[l]) % modulo == k条件的sum[l]是不是已经在哈希表里面了。哈希表map的作用是存放已经枚举过的sum。
#include <vector>
#include <unordered_map>class Solution {
public:long countInterestingSubarrays(std::vector<int>& nums, int modulo, int k) {int n = nums.size();// x是原始数组,sum是前缀和数组std::vector<int> x(n, 0);std::vector<int> sum(n + 1, 0);// 使用unordered_map存储各个余数的位置数量std::unordered_map<int, int> cnt;cnt[0] = 1;long ans = 0;for (int i = 0; i < n; ++i) {if (nums[i] % modulo == k) x[i] = 1;// 计算前缀和sum[i + 1] = (sum[i] + x[i]) % modulo;int r = sum[i + 1];// 此处的索引就是在找满足条件的sum[l],r就是之前版本的sum[r]//需要满足的式子是(sum[r] - sum[l]) % modulo == k//这里+modulo的目的是为了防止r-k是负数,+m再取余,结果还是0不会影响ans += cnt[(r - k + modulo) % modulo];// 更新哈希表中的计数,这里是在更新sum[r]进哈希表(对应之前版本)cnt[r]++;}return ans;}
};