文章目录
- 一、图的概述
- 1.1 图论的作用
- 1.2 图的分类
- 1.2.1 无向图
- 1.2.2 有向图
- 1.2.3 无权图
- 1.2.4 有劝图
- 1.3 图的基本概念
- 二、树的基本表示
- 2.1 邻接矩阵
- 2.1.1 邻接矩阵 表示图
- 2.1.2 邻接矩阵的复杂度
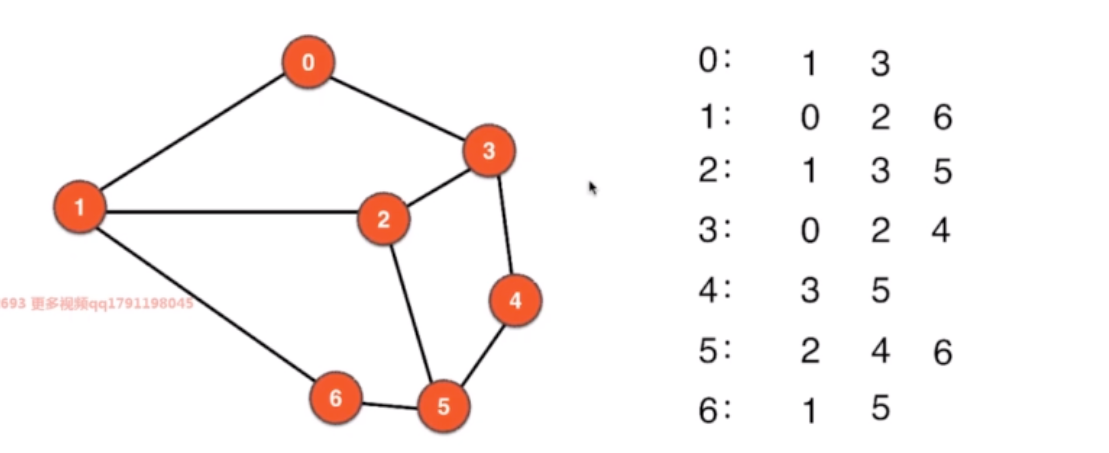
- 2.2 邻接表
- 2.2.1 邻接表的复杂度
- 2.2.2 邻接表By哈希表
- 三、图的深度优先遍历
- 3.1 图深度遍历过程
- 3.2 图遍历改进
- 3.3 先中后
- 3.4 复杂度
- 四、深度遍历的应用
- 4.1 求联通分量
- 4.2 单源路径问题
- 4.3 检测无向图中的环
- 4.4 二分图检测
- 五、图的广度优先遍历
- 六、图论问题的建模
- 七、图论和AI
- 十一、最小生成树
- 11.1 带权图
- 十二、最短路径
- 12.1 迪杰斯特拉算法
- 12.1.1 Dijkstra原理
一、图的概述
1.1 图论的作用






1.2 图的分类


1.2.1 无向图

1.2.2 有向图
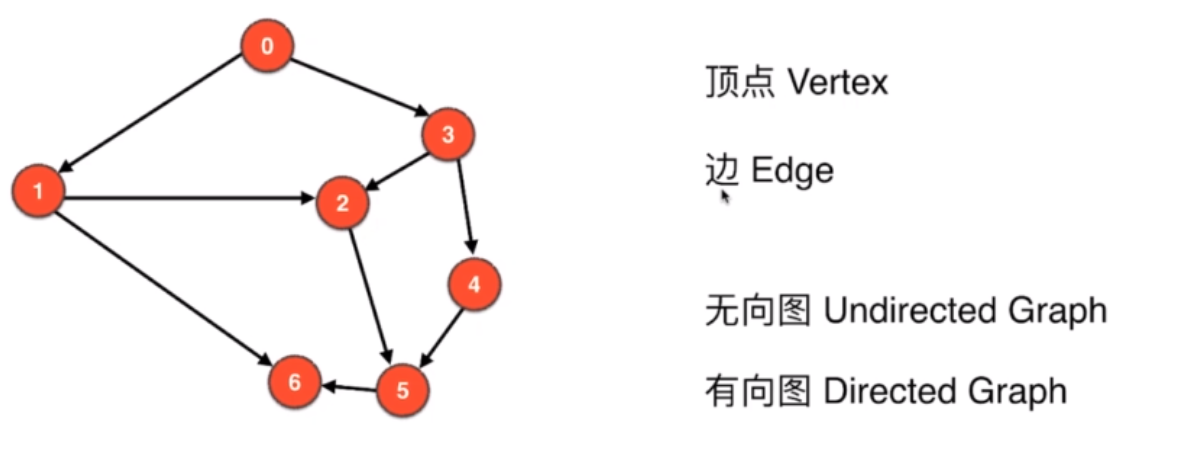
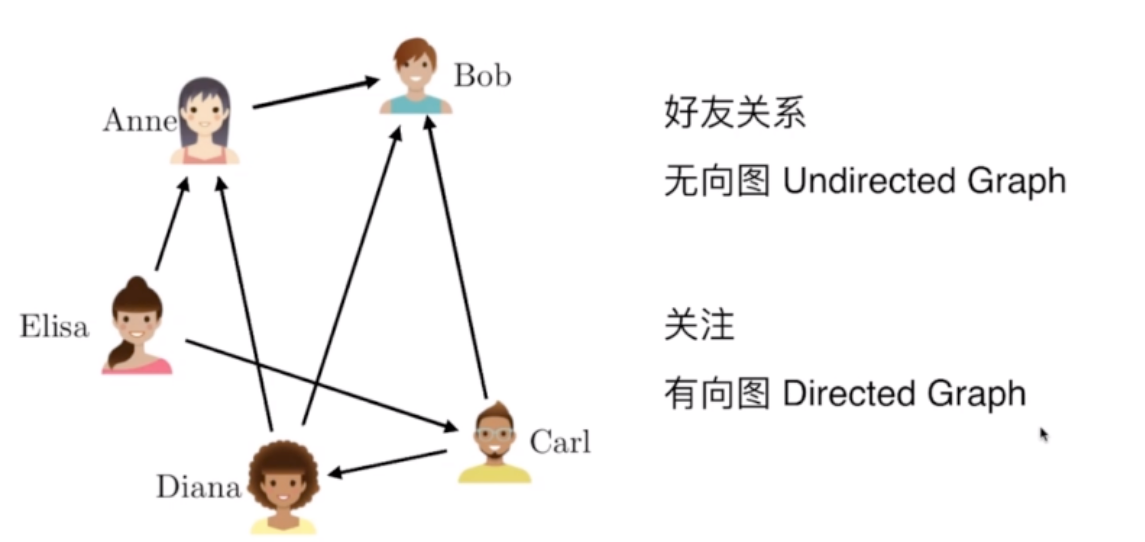
1.2.3 无权图

1.2.4 有劝图

1.3 图的基本概念
- 两点相邻
- 点的邻边
- 路径Path,从一个点到另一个点走过的路
- 环Loop,多个点围城一个圈
- 自环边,自己和自己形成环
- 平行边,重复的边

-
联通分量
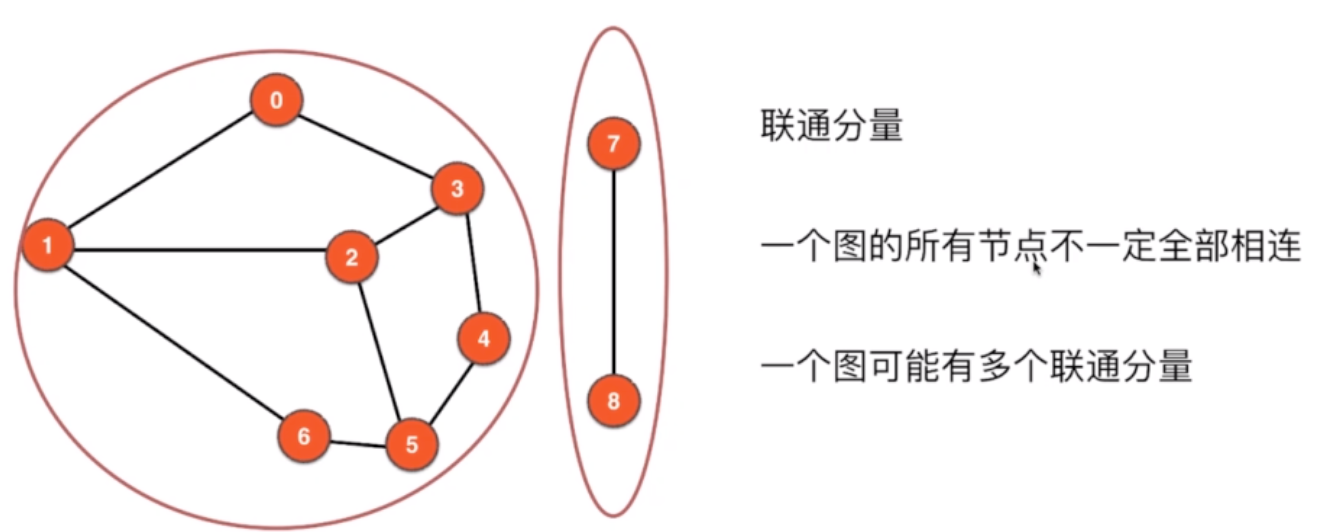
-
无环图

树是一种无环图,一个联通的无环图(一个联通分量)就是树 -
连通图的 生成树

V:顶点数

10) 顶点的度degree
顶点相邻的边数

二、树的基本表示
2.1 邻接矩阵
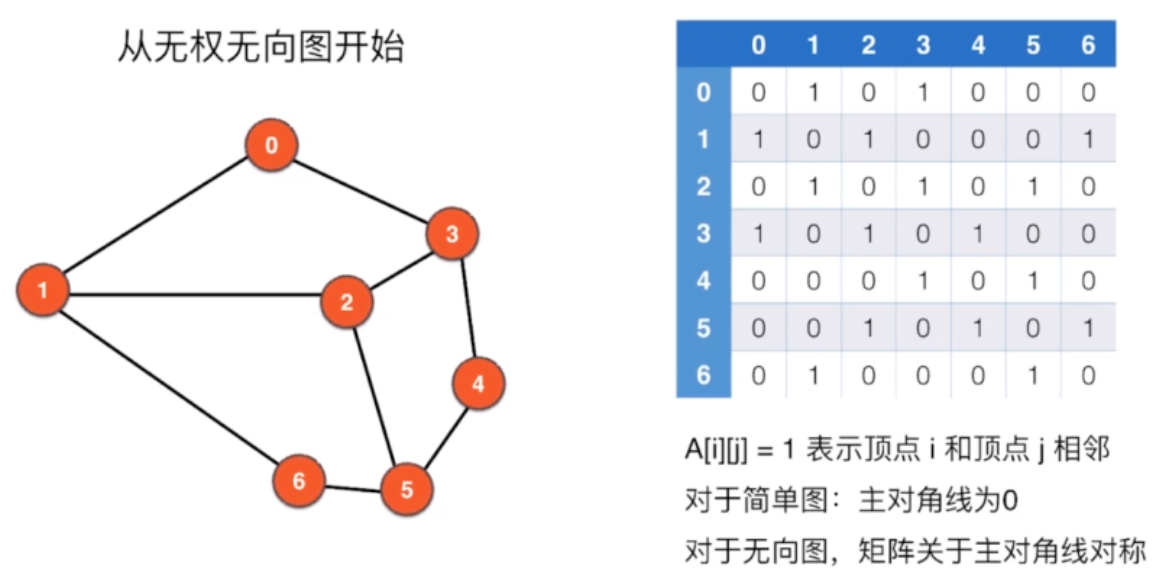

V:顶点数,E:边数
2.1.1 邻接矩阵 表示图
import java.io.*;
import java.util.Scanner;public class AdjMatrix {private int V;private int E;private int[][] adj;public AdjMatrix(String filename){File file = new File(filename);try(Scanner scanner = new Scanner(file)){V = scanner.nextInt();adj = new int[V][V];E = scanner.nextInt();for(int i = 0; i < E; i ++){int a = scanner.nextInt();int b = scanner.nextInt();adj[a][b] = 1;adj[b][a] = 1;}}catch(IOException e){e.printStackTrace();}}@Overridepublic String toString(){StringBuilder sb = new StringBuilder();sb.append(String.format("V = %d, E = %d\n", V, E));for(int i = 0; i < V; i ++){for(int j = 0; j < V; j ++)sb.append(String.format("%d ", adj[i][j]));sb.append('\n');}return sb.toString();}public static void main(String[] args){AdjMatrix adjMatrix = new AdjMatrix("src/main/java/hGraph/base/file/g.txt");System.out.print(adjMatrix);}
} public int V(){return V;}public int E(){return E;}//判断是否有边,两顶点是否相邻public boolean hasEdge(int v, int w){validateVertex(v);validateVertex(w);return adj[v][w] == 1;}
//查找和顶点v相连的顶点public ArrayList<Integer> adj(int v){validateVertex(v);ArrayList<Integer> res = new ArrayList<>();for(int i = 0; i < V; i ++)if(adj[v][i] == 1)res.add(i);return res;}
//查找顶点的度public int degree(int v){return adj(v).size();}
2.1.2 邻接矩阵的复杂度

空间复杂度 可以优化,
求一个点的相邻结点 可以优化
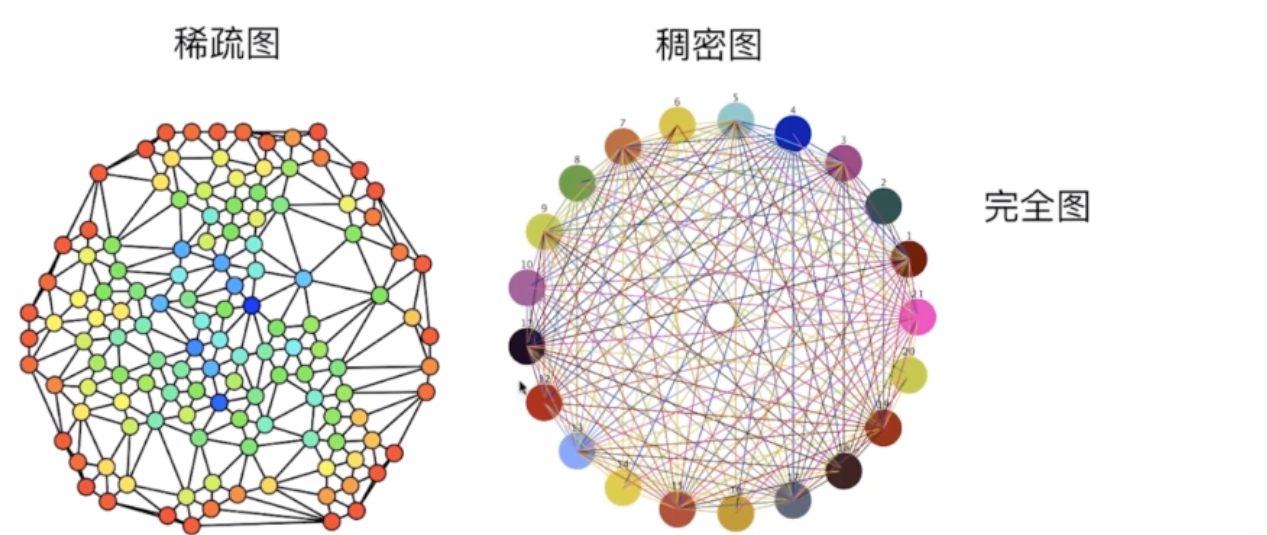
稀疏图&稠密图
根据边的多少
完全图 每个顶点都连接
2.2 邻接表
2.2.1 邻接表的复杂度


2.2.2 邻接表By哈希表

用红黑树实现图
import java.io.File;
import java.io.IOException;
import java.util.TreeSet;
import java.util.Scanner;public class AdjSet {private int V;private int E;private TreeSet<Integer>[] adj;public AdjSet(String pathStr){File file = new File(pathStr);try(Scanner scanner = new Scanner(file)){V = scanner.nextInt();if(V < 0) throw new IllegalArgumentException("V must be non-negative");adj = new TreeSet[V];for(int i = 0; i < V; i ++)adj[i] = new TreeSet<Integer>();E = scanner.nextInt();if(E < 0) throw new IllegalArgumentException("E must be non-negative");for(int i = 0; i < E; i ++){int a = scanner.nextInt();validateVertex(a);int b = scanner.nextInt();validateVertex(b);if(a == b) throw new IllegalArgumentException("Self Loop is Detected!");if(adj[a].contains(b)) throw new IllegalArgumentException("Parallel Edges are Detected!");adj[a].add(b);adj[b].add(a);}}catch(IOException e){e.printStackTrace();}}private void validateVertex(int v){if(v < 0 || v >= V)throw new IllegalArgumentException("vertex " + v + "is invalid");}public int V(){return V;}public int E(){return E;}public boolean hasEdge(int v, int w){validateVertex(v);validateVertex(w);return adj[v].contains(w);}public Iterable<Integer> adj(int v){// public TreeSet<Integer> adj(int v){validateVertex(v);return adj[v];}public int degree(int v){validateVertex(v);return adj[v].size();}@Overridepublic String toString(){StringBuilder sb = new StringBuilder();sb.append(String.format("V = %d, E = %d\n", V, E));for(int v = 0; v < V; v ++){sb.append(String.format("%d : ", v));for(int w : adj[v])sb.append(String.format("%d ", w));sb.append('\n');}return sb.toString();}public static void main(String[] args){AdjSet adjSet = new AdjSet("g.txt");System.out.print(adjSet);}
}三、图的深度优先遍历
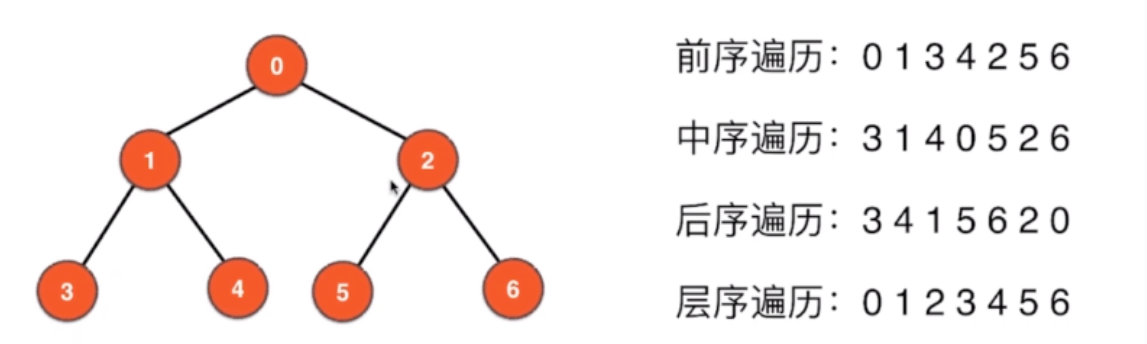
3.1 图深度遍历过程
之前描述过树的遍历
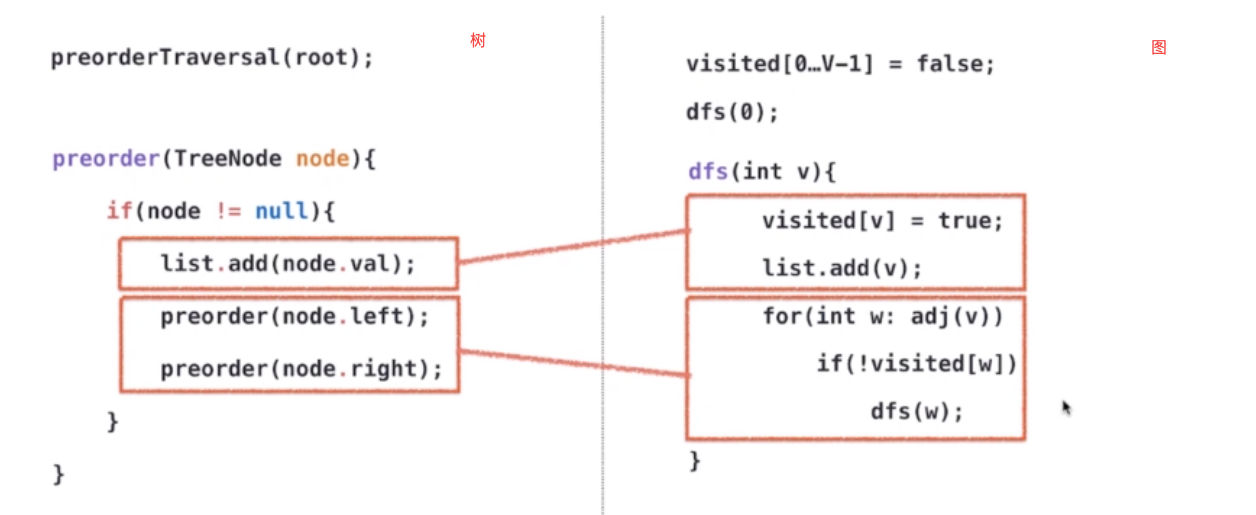



public GraphDFS(Graph G){this.G = G;visited = new boolean[G.V()];dfs(0);}private void dfs(int v){visited[v] = true;order.add(v);for(int w: G.adj(v))if(!visited[w])dfs(w);}
3.2 图遍历改进

不和0 相连 的顶点,就不会遍历
原因是只针对0 调用
改进:对每一个节点进行调用

public GraphDFS(Graph G){this.G = G;visited = new boolean[G.V()];for(int v = 0; v < G.V(); v ++)if(!visited[v])dfs(v);}private void dfs(int v){visited[v] = true;pre.add(v);for(int w: G.adj(v))if(!visited[w])dfs(w);post.add(v);}public Iterable<Integer> pre(){return pre;}public Iterable<Integer> post(){return post;}
3.3 先中后
在树中有先中后遍历

图也可以分为 先 后序遍历

3.4 复杂度
遍历的复杂度:O(V+E)
四、深度遍历的应用
4.1 求联通分量

4.2 单源路径问题
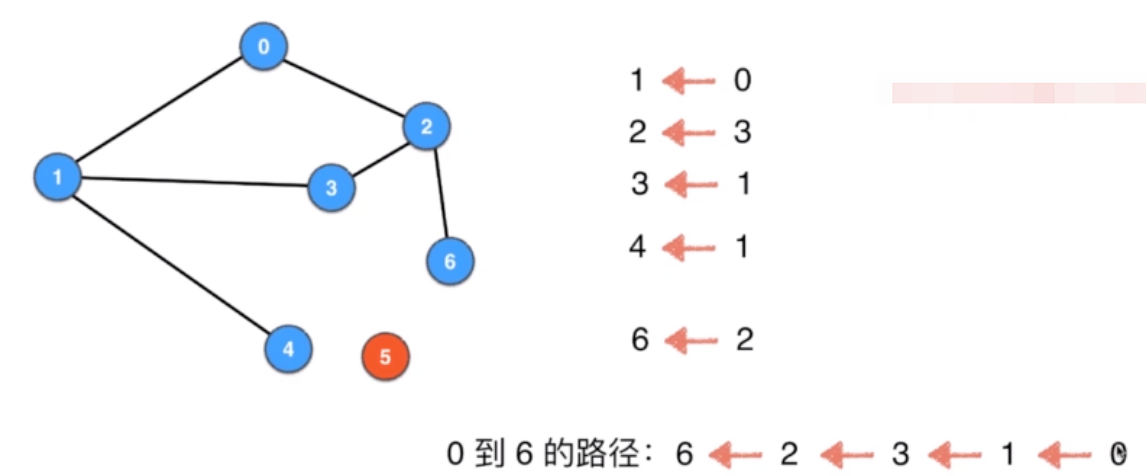
依然做了深度优先遍历,记录这个顶点的pre:从哪里来的
单源路径:从一个顶点出发的路径,不能反向查找
import java.util.ArrayList;
import java.util.Collections;public class SingleSourcePath {private Graph G;private int s;private boolean[] visited;private int[] pre;public SingleSourcePath(Graph G, int s){G.validateVertex(s);this.G = G;this.s = s;visited = new boolean[G.V()];pre = new int[G.V()];dfs(s, s);}private void dfs(int v, int parent){visited[v] = true;pre[v] = parent;for(int w: G.adj(v))if(!visited[w])dfs(w, v);}public boolean isConnectedTo(int t){G.validateVertex(t);return visited[t];}public Iterable<Integer> path(int t){ArrayList<Integer> res = new ArrayList<Integer>();if(!isConnectedTo(t)) return res;int cur = t;while(cur != s){res.add(cur);cur = pre[cur];}res.add(s);Collections.reverse(res);return res;}public static void main(String[] args){Graph g = new Graph("g.txt");SingleSourcePath sspath = new SingleSourcePath(g, 0);System.out.println("0 -> 6 : " + sspath.path(6));System.out.println("0 -> 5 : " + sspath.path(5));}
}
4.3 检测无向图中的环

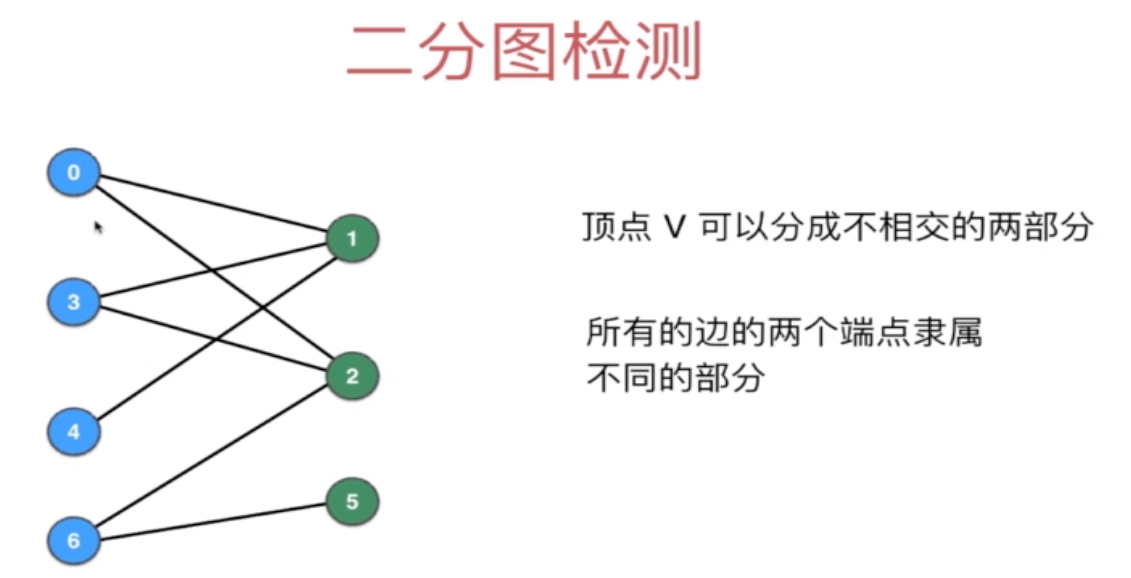
4.4 二分图检测
二分图:
五、图的广度优先遍历

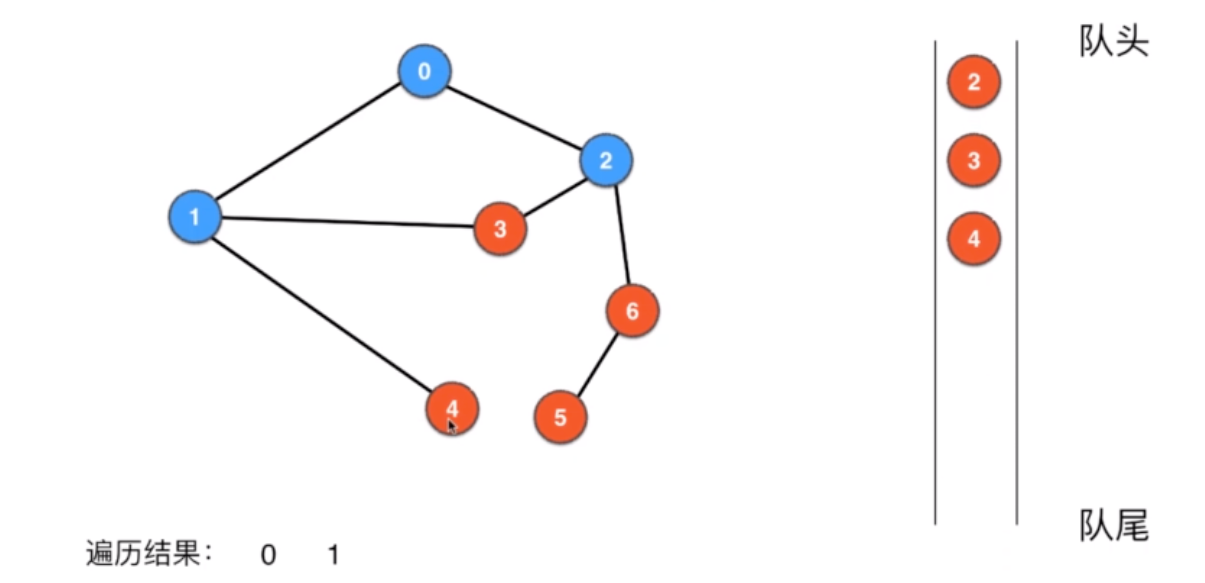

public GraphBFS(Graph G){this.G = G;visited = new boolean[G.V()];for(int v = 0; v < G.V(); v ++)if(!visited[v])bfs(v);}private void bfs(int s){Queue<Integer> queue = new LinkedList<>();queue.add(s);visited[s] = true;while(!queue.isEmpty()){int v = queue.remove();order.add(v);for(int w: G.adj(v))if(!visited[w]){queue.add(w);visited[w] = true;}}}public Iterable<Integer> order(){return order;}
复杂度:O(V+E)
六、图论问题的建模
七、图论和AI
十一、最小生成树
11.1 带权图
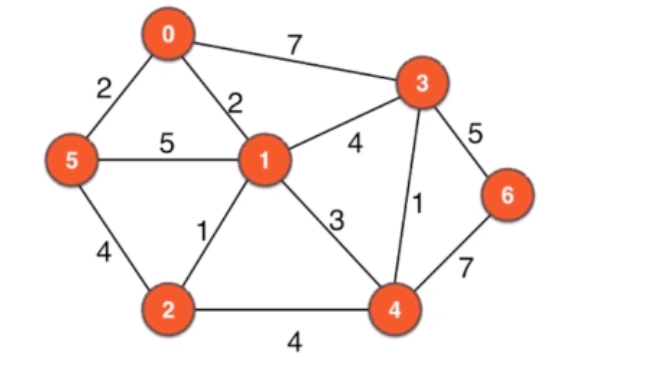
/// 暂时只支持无向带权图
public class WeightedGraph implements Cloneable{private int V;private int E;private TreeMap<Integer, Integer>[] adj;public WeightedGraph(String filename){File file = new File(filename);try(Scanner scanner = new Scanner(file)){V = scanner.nextInt();if(V < 0) throw new IllegalArgumentException("V must be non-negative");adj = new TreeMap[V];for(int i = 0; i < V; i ++)adj[i] = new TreeMap<Integer, Integer>();E = scanner.nextInt();if(E < 0) throw new IllegalArgumentException("E must be non-negative");for(int i = 0; i < E; i ++){int a = scanner.nextInt();validateVertex(a);int b = scanner.nextInt();validateVertex(b);int weight = scanner.nextInt();if(a == b) throw new IllegalArgumentException("Self Loop is Detected!");if(adj[a].containsKey(b)) throw new IllegalArgumentException("Parallel Edges are Detected!");adj[a].put(b, weight);adj[b].put(a, weight);}}catch(IOException e){e.printStackTrace();}}
十二、最短路径
带权图的最短路径不一定 走的边最少

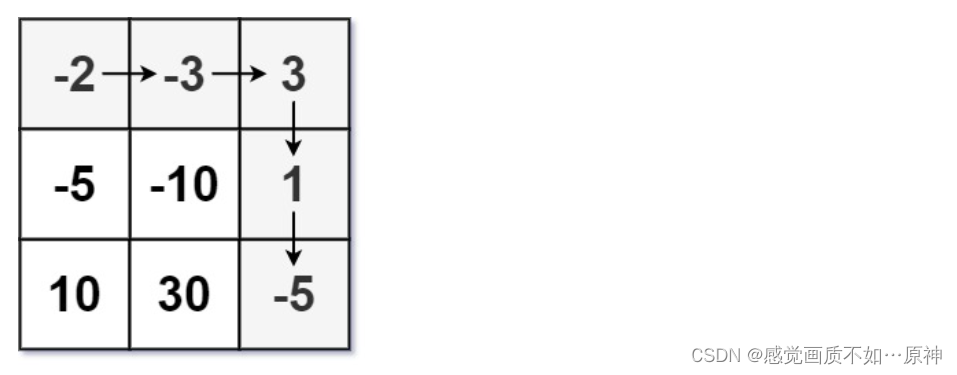
12.1 迪杰斯特拉算法
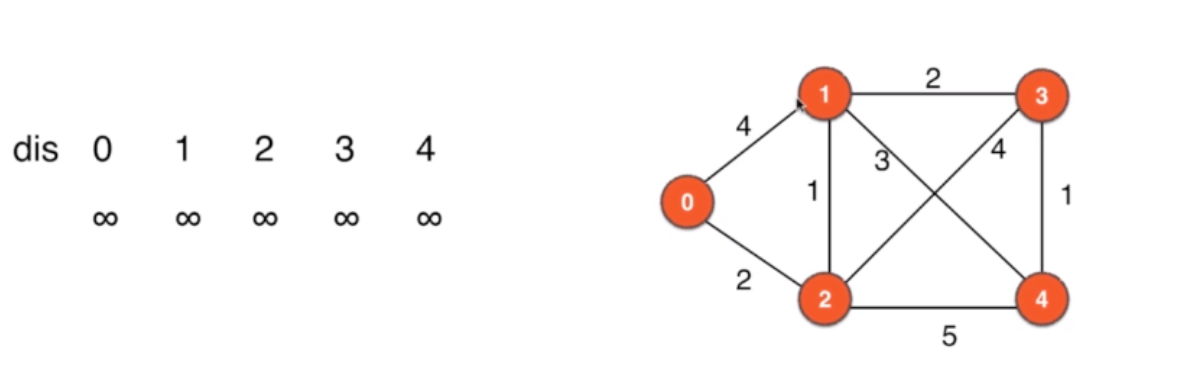
12.1.1 Dijkstra原理
-
指定dis:源到各个顶点的路径,先初始为MAX
-
找顶点,更新dis

-
找当前最短的路径,确定这个就是到顶点的最短路径:确定2位0到2的最短路径
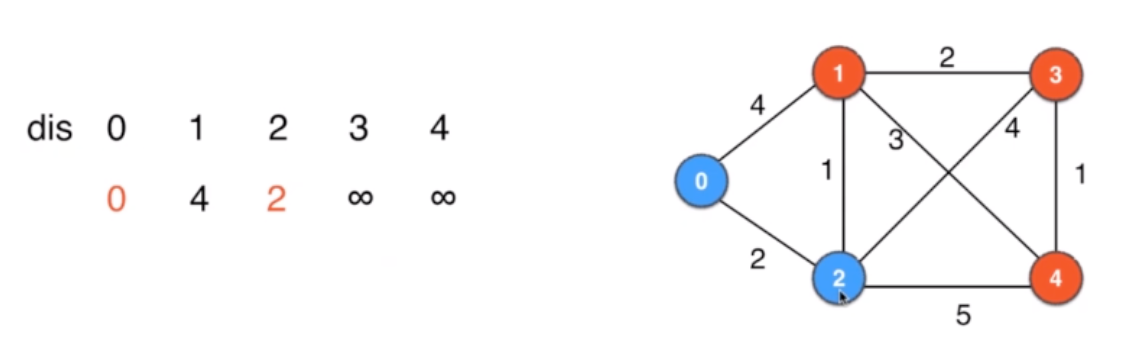
-
根据2顶点,来做更新
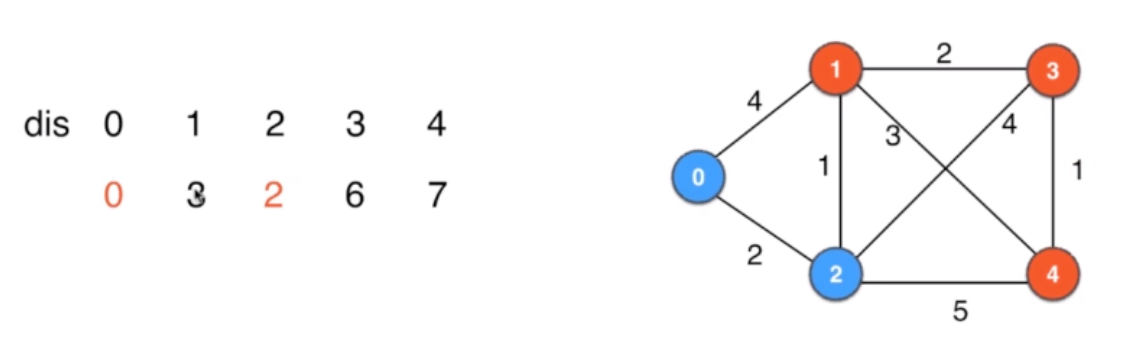
这里更新了2 到各个顶点的路径,1 从 4 更新到了3 -
再从当前的路径中找最小的,为3 顶点1,
所以确定顶点1 的最短路径为3

- 再根据顶点1 ,更新dis

- 确定当前最短的距离为5 ,顶点3

- 更新dis,到顶点4都为6

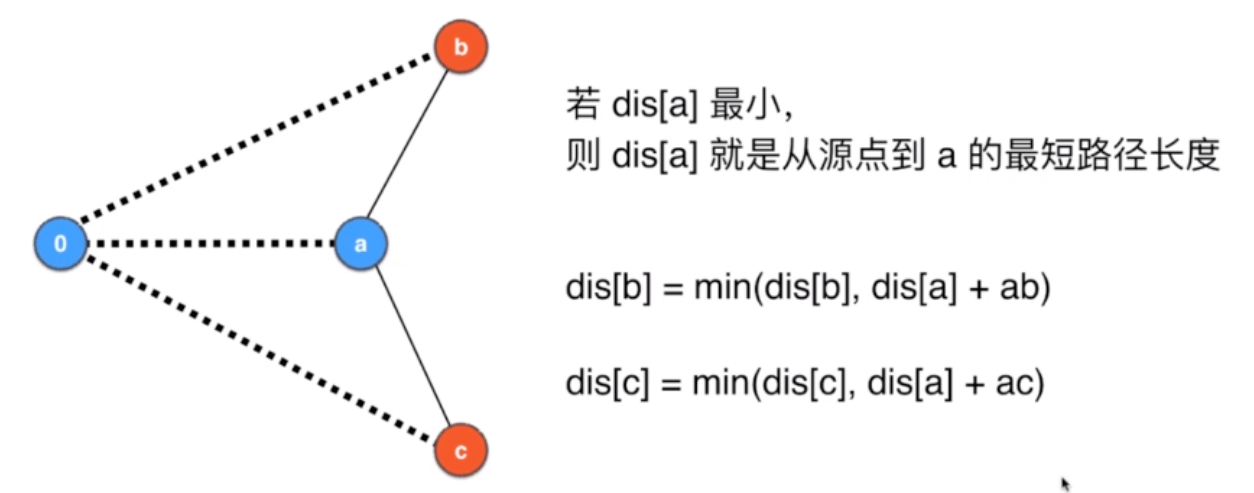
每轮循环:
- 初始化源到其他顶点的dis,默认都为MAX
- 找到当前没有访问的最短路节点
- 确定这个节点的最短路径就是当前大小
- 根据这个节点的最短路径大小,更新到其他节点的路径长度,如果比dis中的要小,那么就更新dis
#from ChatGPT
1.初始化距离数组dist和标记数组visited。将起始地点设置为起点,其他地点的距离初始化为无穷大,visited数组初始化为false。
2.从起点开始遍历所有地点,选择当前距离最小且未被访问过的地点u。
3.对于地点u,更新与其相邻的地点v的距离,如果新的距离小于原来的距离,则更新距离数组dist和路径数组path。
4.标记地点u为已访问,重复上述过程,直到所有地点都被访问。
5.最终得到起点到每个地点的最短距离和路径。