前言
经常会有面试题看到这样的问题 “ select count(*) ”, “ select count(field1) ”, “ select count(1) ” 的效率差异啥的
然后 我们这里 就来探索一下 这个问题
我们这里从比较复杂的 select count(field1) 开始看, 因为 较为复杂的处理过程 会留一下一些关键的调试的地点, 然后根据这些地点去参照看一下 其他的查询 在这些地点分别都是怎么做的?
“ select count(field1) ” 的实现
首先是语法解析这边, 将 field1 解析为一个 PTI_in_sum_expr 里面包含了 field1 的 token 和 location 等等
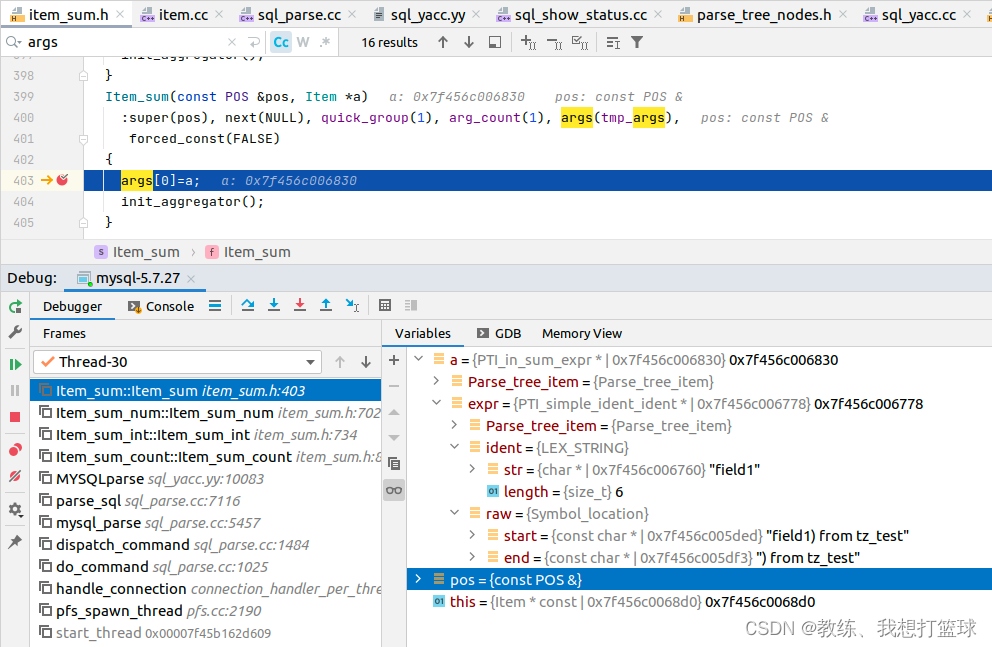
然后就是后面将 PTI_in_sum_expr resolve 成为 Item_field, 当然 这里也仅仅是维护了 field1 的 token 的相关信息, 后面才会填充 table 等等信息

然后是根据上下文填充目标字段的 table 的信息, field 的信息
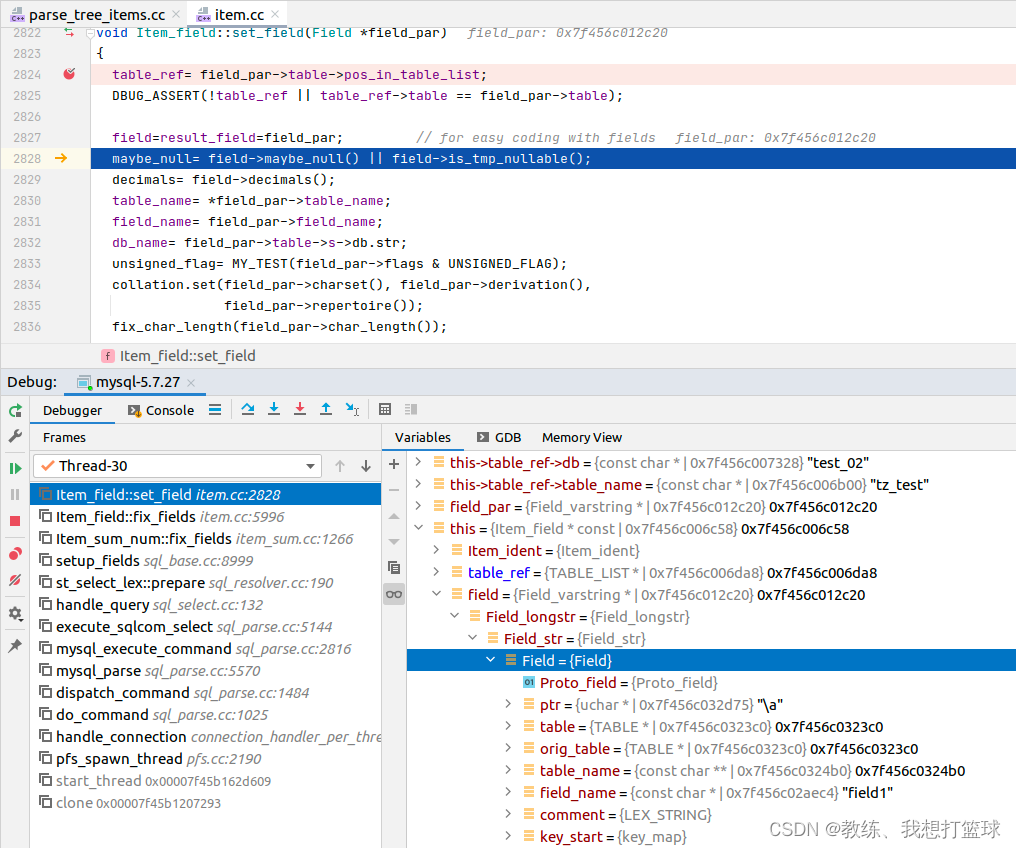
然后就是迭代符合条件的记录, 然后根据给定的字段是否为空的信息, 来判断是否统计计数
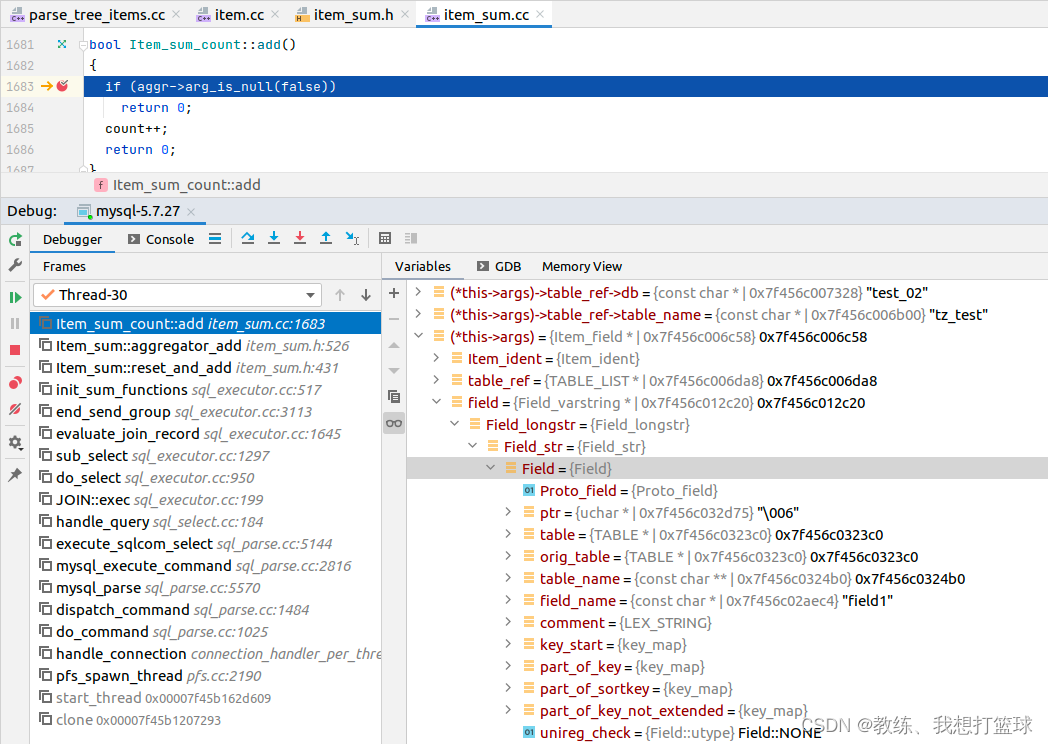
然后判断 是否为空的标准为, 字段值是否是 NULL
对应的处理方式如下
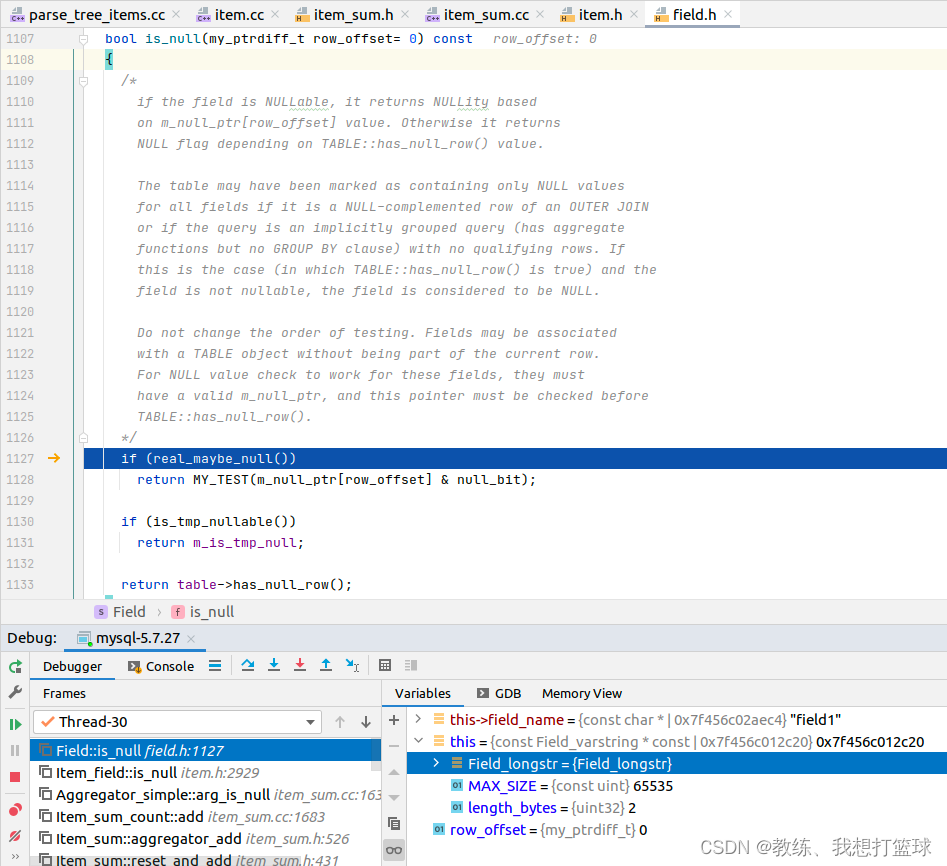
“ select count(*) ” 的实现
首先是语法解析这边, 将 * 解析为 NULL, 这里上下文包含了 location 的相关信息

sql 解析完成之后, args[0] 之前为 NULL, 被更新为了 “Item_int(0)”
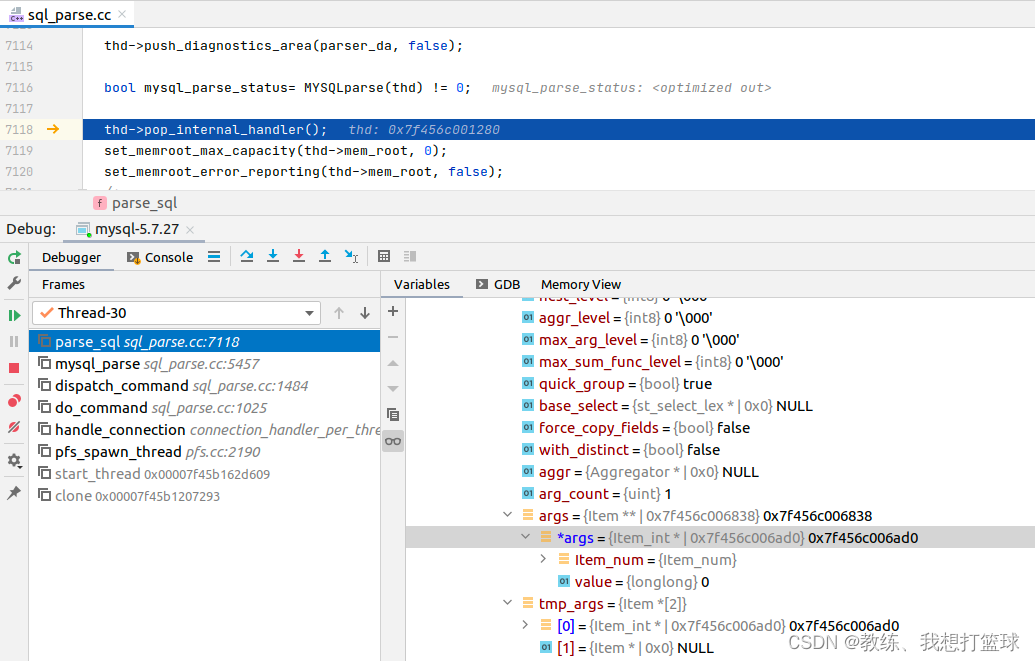
然后 setup_fields 这边, 没有做 太多的事情, Item_int 这边的 fix_fields 这边是走的默认处理 Item::fix_fields

Item::fix_fields 的处理如下, 仅仅是一个标记的更新
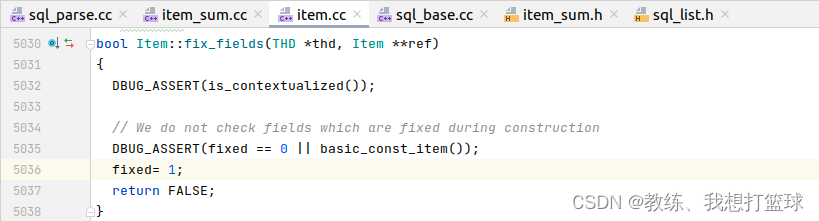
然后就是迭代符合条件的记录, 然后根据给定的字段是否为空的信息, 来判断是否统计计数
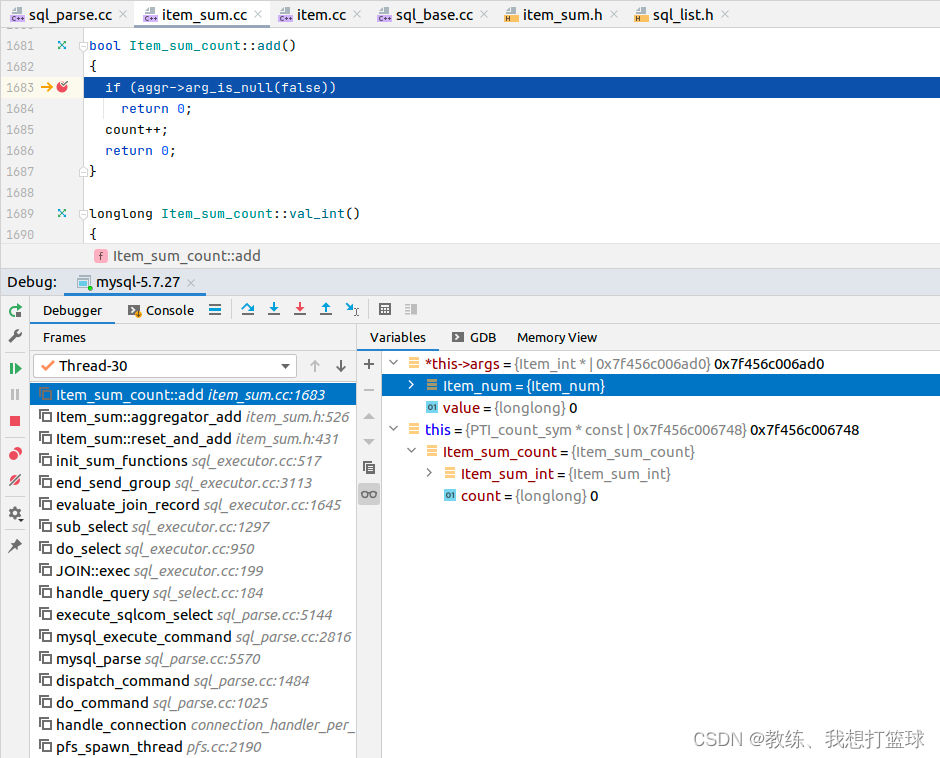
判断是否为空的判断标注哪位, 恒不为空
类似于一个基本数据类型的 int 值为 0, 恒不为 NULL
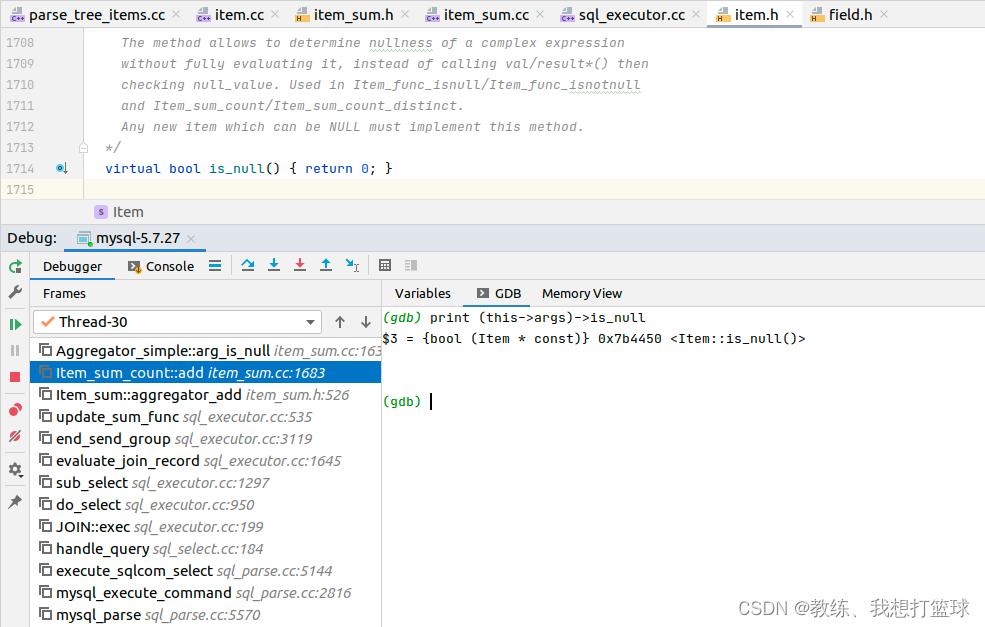
“ select count(1) ” 的实现
首先是语法解析这边, 将 1 解析为 PTI_in_sum_expr 里面 PTI_num_literal_num 包含了长了常量 ”1”, 这里上下文包含了 location 的相关信息
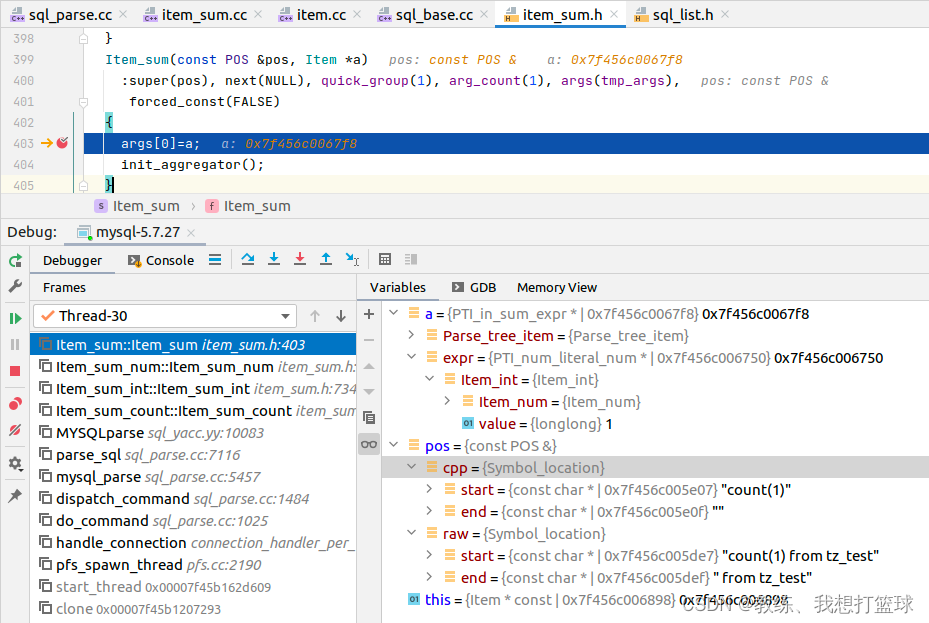
然后 setup_fields 这边, 没有做 太多的事情, Item_int 这边的 fix_fields 这边是走的默认处理 Item::fix_fields
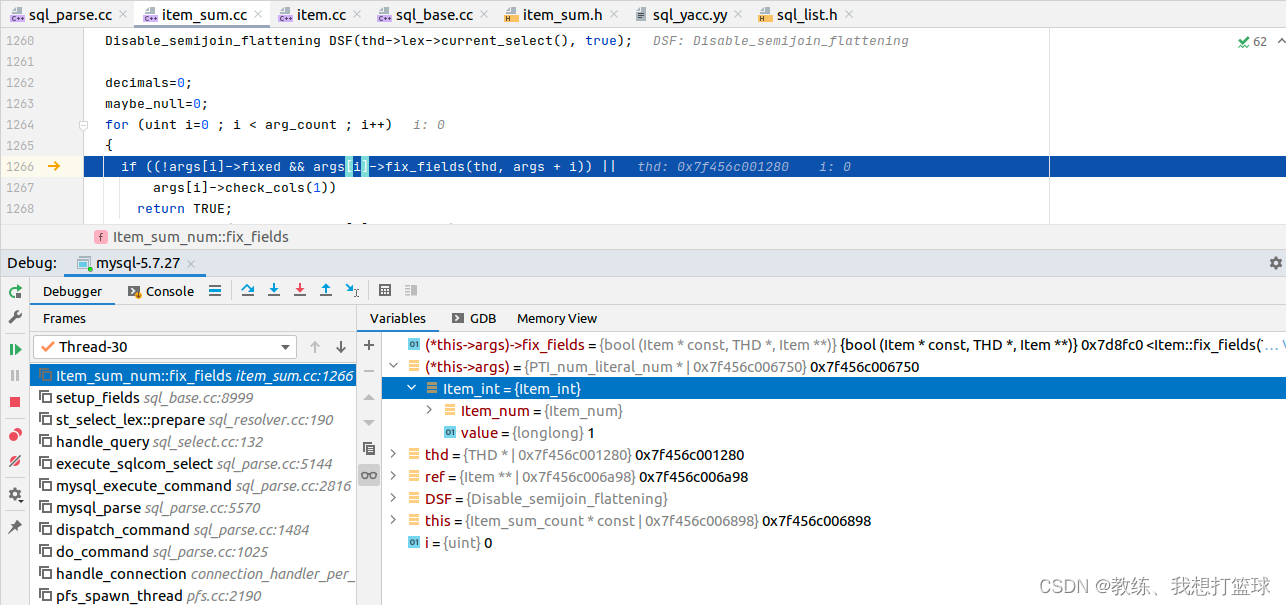
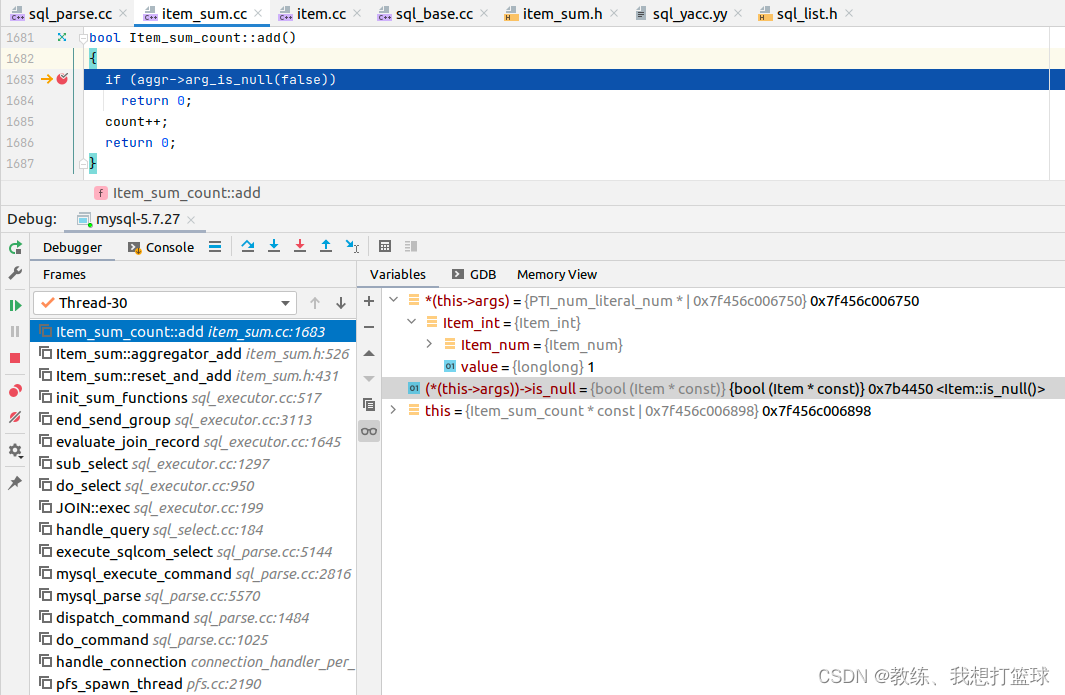
然后就是迭代符合条件的记录, 然后根据给定的字段是否为空的信息, 来判断是否统计计数
PTI_num_literal_num 这边判断为不为空的方式也是基于 Item::is_null, 也是恒不为空
“ select count(“1“) ” 的实现
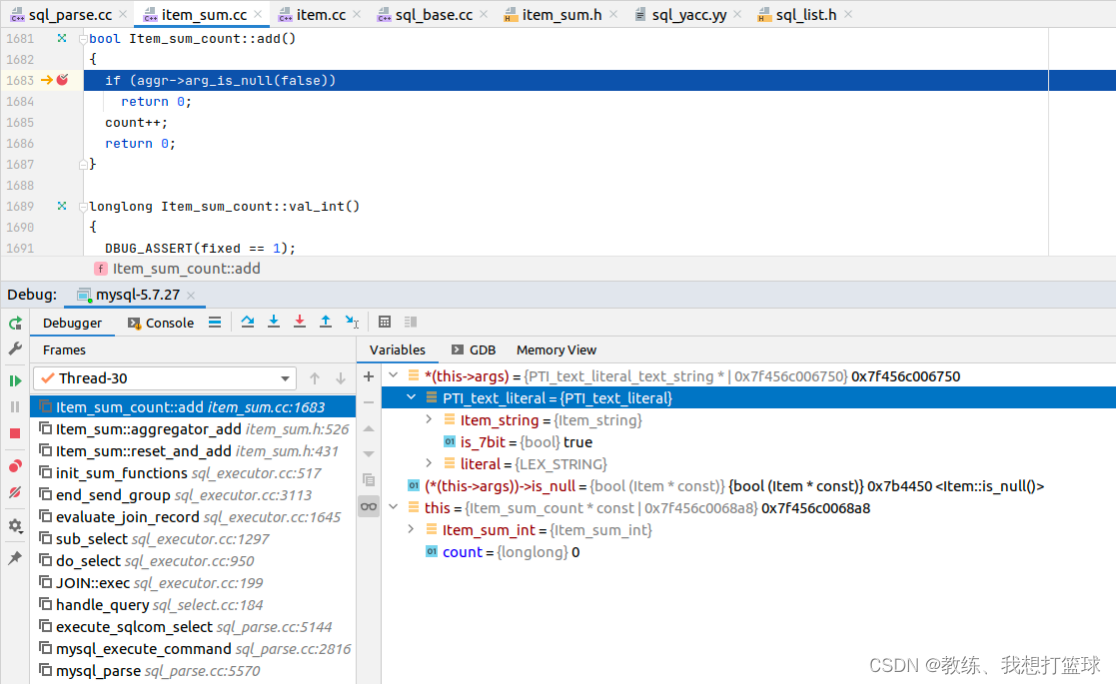
其他的我们就不去看了, 仅仅看一下 Item_sum_count::add 这边的上下文
解析出来的 对象有所调整, 但是结果不变, PTI_text_literal_text_string 这边判断为不为空的方式也是基于 Item::is_null, 也是恒不为空
“ select count(NULL) ” 的实现
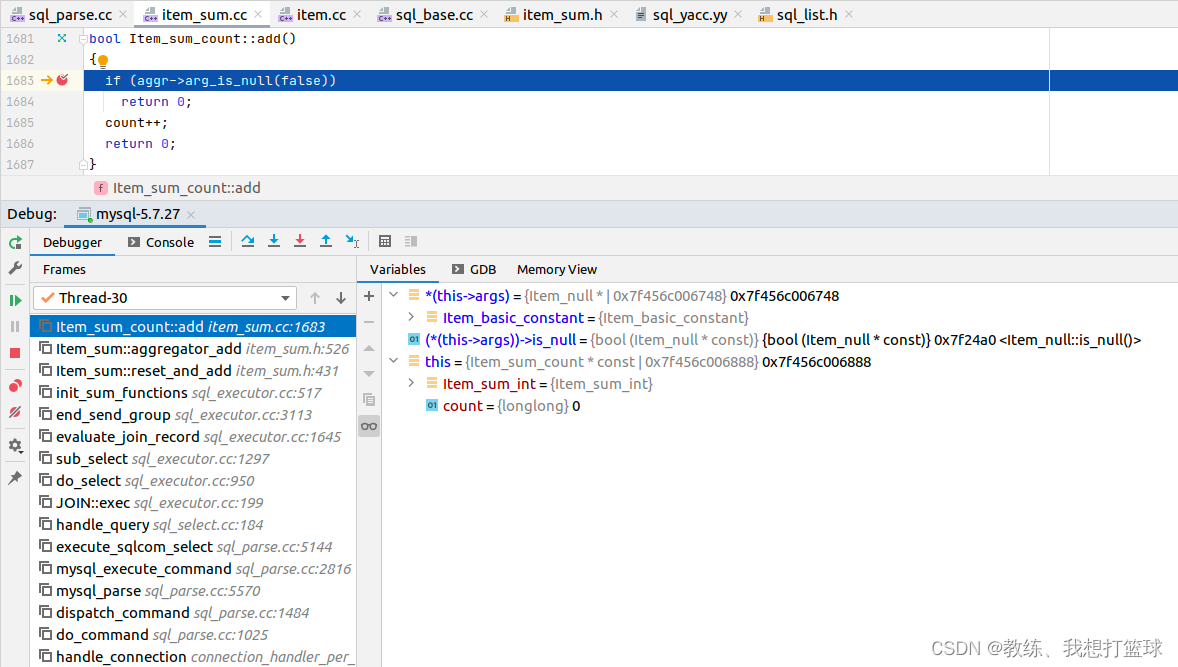
其他的我们就不去看了, 仅仅看一下 Item_sum_count::add 这边的上下文
解析出来的 对象有所调整, 但是结果不变, Item_null 这边判断为不为空的方式是基于 Item_null::is_null, 是恒为空
因此 最终的查询结果为 0
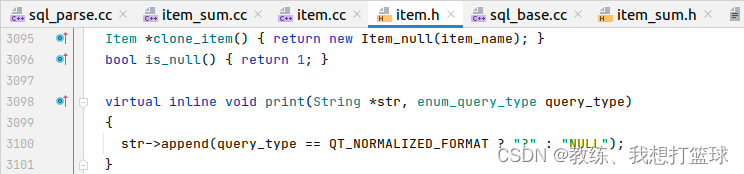
然后 Item_null::is_null 的处理方式如下, 恒为空
总结
大致可以分成两类, “ select count(field1) ” 和 ”其他select count”
影响效率的差异主要在于 是否是全表扫描, 扫描的是聚簇索引还是非聚簇索引
假设是索引扫描, 则几者的差异并不大, 主要的差异在于 比较的时候前者复杂一点, 后者快一点, 但是扫描的记录数量有限, 效率影响不大
假设是全表扫描, 主要的影响就是 “ select count(field1) ” 是走聚簇索引, 还是非聚簇索引了, 然后 “其他select count” 会优先选择较小的非聚簇索引, 造成的影响主要是 io 的开销, 走非聚簇索引所需要的 io 较小
完