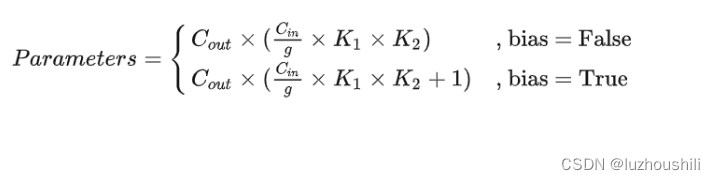方差是统计学中用来衡量数据集合中数值分散或离散程度的一种统计量。它表示了数据点与数据集合均值之间的差异程度,即数据的分散程度。方差越大,表示数据点更分散,而方差越小,表示数据点更集中。
方差的计算公式如下:
需要注意的是,总体方差的计算中除以的是总体数据点的数量 N,而样本方差的计算中除以的是 n−1(自由度,通常用来估计总体方差)。这是为了校正由于使用样本估计总体方差而引入的偏差。
方差是统计分析中的重要概念,它有助于了解数据的离散程度和变异性。在许多统计方法中,方差被用来进行假设检验和方差分析等分析。在实际应用中,方差通常与标准差(方差的平方根)一起使用,以更直观地表示数据的分散情况。
方差分析(Analysis of Variance,简称ANOVA)是一种统计方法,用于比较三个或三个以上组(或处理)之间的均值是否存在显著差异。它是一种用于处理多个组之间差异的方法,通常用于以下情况:
- 比较多个处理组(例如,不同药物的疗效,不同肥料的生长效果等)是否具有统计显著性。
- 比较多个因素对于一个连续的响应变量(因变量)是否有显著影响,例如,考察不同年份、不同地区和不同气象因素对于农作物产量的影响。
方差分析的主要思想是将总体方差分解为组内方差(Within-group variance)和组间方差(Between-group variance)。如果组间方差显著大于组内方差,那么就可以得出至少有一个组的均值存在显著差异。
在方差分析中,通常有三种常见的类型:
-
单因素方差分析(One-Way ANOVA):用于比较一个因素对于一个连续变量的影响,例如比较不同药物剂量对于治疗效果的影响。
-
双因素方差分析(Two-Way ANOVA):用于比较两个因素对于一个连续变量的影响,通常包括两个独立变量,例如考察不同肥料类型和不同浇水频率对于植物生长的影响。
-
多因素方差分析(Multifactor ANOVA):用于比较多个因素对于一个连续变量的影响,可以包括多个独立变量,以考察多个因素的联合影响。
进行方差分析时,需要注意以下几点:
-
方差分析依赖于方差齐性假设,即各组的方差相等。如果不满足方差齐性假设,可以考虑使用非参数方法或进行方差齐性的检验。
-
方差分析结果通常包括F统计量和p-value,用于判断组均值之间的差异是否显著。
-
如果ANOVA表明存在显著差异,通常需要进行进一步的事后比较(post hoc tests)来确定哪些组之间存在差异。常见的事后比较方法包括Tukey's Honestly Significant Difference(Tukey's HSD)和Bonferroni校正等。
方差分析是一种有用的统计工具,用于分析多个组之间的差异,但在使用时需要仔细考虑实验设计、假设检验和数据的前提条件。
方差分析的主要思想是通过将总体方差分解为组内方差和组间方差来检测组均值之间的显著性差异。这个思想是方差分析的核心概念,通常被称为"方差分解"。
具体来说,方差分析的基本原理是将观测值的变异性分为两部分:
-
组内变异性(Within-group variance):这是由于组内个体之间的随机变异所引起的差异。组内方差衡量了每个组内部的数据点与组内均值之间的离散程度。它反映了随机误差或未解释的变异性。
-
组间变异性(Between-group variance):这是由于不同组之间的差异所引起的差异。组间方差衡量了各组均值之间的差异,也就是不同组之间的离散程度。
如果组间方差显著大于组内方差,那么意味着不同组之间的均值差异较大,可以得出至少有一个组的均值存在显著差异。这时,我们可以拒绝原假设,认为组均值之间存在显著差异。
方差分析通常会生成F统计量(F-statistic),用来比较组间方差与组内方差的比值。通过F统计量和p-value,可以进行假设检验,以确定是否拒绝原假设,即组均值相等的假设。
方差分析是用于比较多个组均值之间差异的强大工具,它有助于确定哪些组或处理之间存在显著差异,从而帮助研究人员进行更深入的数据分析和假设检验。
F统计量是方差分析中的核心统计量,用于比较组间方差与组内方差的比值,以进行假设检验,以确定是否拒绝原假设。
F统计量的计算公式如下:
F=组间方差(Between-group variance)/ 组内方差(Within-group variance)
F统计量的值越大,意味着组间差异相对于组内差异更显著。在方差分析中,我们使用F统计量来进行以下假设检验:
- 原假设(H0):组均值相等,即各组之间没有显著差异。
- 备择假设(Ha):至少有一个组的均值存在显著差异。
我们通过计算F统计量的值以及对应的p-value来进行假设检验。如果F统计量的值远远大于1,而p-value小于显著性水平(通常为0.05),则我们可以拒绝原假设,得出至少有一个组的均值存在显著差异的结论。如果p-value大于显著性水平,我们则不拒绝原假设,认为没有足够的证据表明组均值之间存在显著差异。
方差分析中的F统计量和p-value提供了一个有效的方式来量化组均值之间的差异,这对于确定因素对于观察结果的影响是否显著具有重要意义。当进行方差分析时,通常还会进行事后比较以确定哪些组之间存在显著差异。
import pandas as pd
import scipy.stats as stats
import statsmodels.api as sm
from statsmodels.formula.api import ols
import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 防止中文标签乱码,还有通过导入字体文件的方法
plt.rcParams['axes.unicode_minus'] = False# 创建示例数据集
data = pd.DataFrame({'Method': ['A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'C', 'C', 'C', 'C'],'Size': [10.2, 10.5, 9.8, 10.0, 9.0, 9.2, 8.8, 9.1, 11.0, 11.2, 11.5, 11.1]
})# 数据摘要统计和可视化
summary = data.groupby('Method')['Size'].describe()
print(summary)# 箱线图可视化
plt.figure(figsize=(8, 6))
sns.boxplot(x='Method', y='Size', data=data)
plt.title('尺寸分布箱线图')
plt.xlabel('生产方法')
plt.ylabel('尺寸')
plt.show()# 方差分析
model = ols('Size ~ Method', data=data).fit()
anova_table = sm.stats.anova_lm(model, typ=2)
print("\n方差分析结果:\n", anova_table)# 方差分析结果可视化
plt.figure(figsize=(8, 6))
sns.barplot(x='Method', y='Size', data=data, ci=None)
plt.title('各生产方法下的平均尺寸')
plt.xlabel('生产方法')
plt.ylabel('平均尺寸')
plt.show()# 方差分析结果解释
alpha = 0.05
p_value = anova_table['PR(>F)'][0]
if p_value < alpha:print("\n在显著性水平0.05下,不同生产方法对产品尺寸存在显著影响。")
else:print("\n在显著性水平0.05下,不拒绝原假设,即不同生产方法对产品尺寸没有显著影响。")在这个示例中,我们首先创建了一个示例数据集,其中包含不同生产方法下的产品尺寸数据。然后,我们进行了数据摘要统计和可视化,包括描述性统计和箱线图。接下来,我们使用方差分析(ANOVA)来分析不同生产方法对产品尺寸是否存在显著影响。最后,我们根据方差分析结果解释了不同生产方法的影响。
这个示例展示了如何使用Python进行方差分析,并解释了结果,以确定不同因素对于产品尺寸的影响是否显著。根据结果,生产方法是否显著影响产品尺寸将决定制造过程是否需要进行调整或优化。