【分类】分类性能评价

评价指标

1、准确率、召回率、精确率、F-度量、ROC

属于各类的样本的并不是均一分布，甚至其出现概率相差很多个数量级，这种分类问题称为不平衡类问题。在不平衡类问题中，准确率并没有多大意义，我们需要一些别的指标。

通常在不平衡类问题中，我们使用F-度量来作为评价模型的指标。以二元不平衡分类问题为例，预测只可能出现4种状况：

a) 将正类样本预测为正类（True Positive, TP） b) 将负类样本预测为正类（False Positive, FP）

c) 将正类样本预测为负类（False Negative, FN） d) 将负类样本预测为负类（True Negative, TN）
在这里插入图片描述

对于测试集中 $N$ 个样本，有 $M$ 个被正确分类，则准确率(正确率)为：

$=\frac{M}{N}$

定义召回率（recall）：不能接受漏报,预测到所有想被预测到的样本

$召回率(recall)=\frac{被预测为正类的}{原本的正类}=\frac{|TP|}{|TP|+|FN|}$

定义精确率(precision)：不能接受误检,预测结果尽可能不出错
$精确率(precision)=\frac{被预测为正类的}{预测的正类}=\frac{|TP|}{|TP|+|FP|}$
$F$ -度量则是在召回率与精确率之间去调和平均数；
$F_{ \alpha}=\frac{(1+\alpha ^2)RP}{R+\alpha P}\\ F_{1}=\frac{2RP}{R+P}$

精确率：分母是预测到的正类，精确率的提出是让模型的现有预测结果尽可能不出错(宁愿漏检，也不能让现有的预测有错)

以地震模型为例说就是宁愿地震了没报，也不能误报地震，比如说为了不错报，只预测了第50天可能发生地震，此时的

1.精确率：1/1=100%

2.召回率：1/2=50%

虽然有一次地震没预测到，但是我们做出的预测都是对的。

召回率：分母是原本的正类，召回率的提出是让模型预测到所有想被预测到的样本(就算多预测一些错的，也能接受)

以地震模型为例说这100次地震，比如说为了不漏报，预测了第30天、50天、51天、70天、85天地震，此时的

1.精确率：2/5=40%

2.召回率：2/2=100%

虽然预测错了3次，但是我们把会造成灾难的2次地震全预测到了。

精确率和召回率有什么用？为什么需要它？通俗讲解(人话)

上面我们已经讲的很清楚了，这里以两种需求为例

预测地震 - 不能接受漏报
人脸识别支付(银行人脸支付) - 不能接受误检

人脸识别支付：主要提升精确率，更倾向于不能出现错误的预测。

应用场景：你刷脸支付时就算几次没检测到你的脸，最多会让你愤怒，对银行损失不大，但是如果把你的脸检测成别人的脸，就会出现金融风险，让别人替你买单，对银行损失很大。所以宁愿让你付不了钱，也不会让别人帮你付钱。

预测地震：主要提升召回率，更倾向于宁愿多预测一些错的也不能漏检。

应用场景：地震预测时宁愿多预测一些错的，也不想漏掉一次地震，预测错误最多会让大家多跑几趟，造成少量损失。只要预测对一次，就会挽回百亿级别的损失，之前所有的损失都值了。

ROC曲线(Receiver Operating Characteristic,受试者操作特征)
通常情况下，我们希望ROC曲线越靠近左上角，这表示模型在各种阈值下都表现良好，同时具有高的真正率和低的假正率，而AUC值（曲线下面积）也可以用来衡量模型的整体性能，越接近1表示模型性能越好。

画ROC曲线步骤：

根据分类模型得出每个样本属于正类的概率，根据概率将样本由高到低排列
将样本为正类的概率由高到低，依次作为阈值 $t$ ，大于等于 $t$ 则为正类，小于t视为反类
使用真正率 $TPR=\frac{TP}{TP+FN}$ 作为竖轴，假正率 $FPR=\frac{FP}{FP+TN}$ 作为横轴，对于每个选定的阈值均能产生一个对应的点。

例子：

样本编号	分类	预测为正类的概率	TPR	FPR
1	正类	0.98	$\frac{1}{1+14}=\frac{1}{15}$	$\frac{0}{0+5}=\frac{0}{5}$
2	正类	0.96	$\frac{2}{2+13}=\frac{2}{15}$	$\frac{0}{0+5}=\frac{0}{5}$
3	正类	0.92	$\frac{3}{3+12}=\frac{3}{15}$	$\frac{0}{0+5}=\frac{0}{5}$
4	正类	0.88	$\frac{4}{4+11}=\frac{4}{15}$	$\frac{0}{0+5}=\frac{0}{5}$
5	正类	0.85	$\frac{5}{5+10}=\frac{5}{15}$	$\frac{0}{0+5}=\frac{0}{5}$
6	正类	0.83	$\frac{6}{6+9}=\frac{6}{15}$	$\frac{0}{0+5}=\frac{0}{5}$
7	反类	0.82	$\frac{6}{6+9}=\frac{6}{15}$	$\frac{1}{1+4}=\frac{1}{5}$
8	正类	0.8	$\frac{7}{7+8}=\frac{7}{15}$	$\frac{1}{1+4}=\frac{1}{5}$
9	正类	0.78	$\frac{8}{8+7}=\frac{8}{15}$	$\frac{1}{1+4}=\frac{1}{5}$
10	反类	0.71	$\frac{8}{8+7}=\frac{8}{15}$	$\frac{2}{2+3}=\frac{2}{5}$
11	正类	0.68	$\frac{9}{9+6}=\frac{9}{15}$	$\frac{2}{2+3}=\frac{2}{5}$
12	正类	0.64	$\frac{10}{10+5}=\frac{10}{15}$	$\frac{2}{2+3}=\frac{2}{5}$
13	正类	0.59	$\frac{11}{11+4}=\frac{11}{15}$	$\frac{2}{2+3}=\frac{2}{5}$
14	正类	0.55	$\frac{12}{12+3}=\frac{12}{15}$	$\frac{2}{2+3}=\frac{2}{5}$
15	反类	0.52	$\frac{12}{12+3}=\frac{12}{15}$	$\frac{3}{3+2}=\frac{3}{5}$
16	正类	0.51	$\frac{13}{13+2}=\frac{13}{15}$	$\frac{3}{3+2}=\frac{3}{5}$
17	正类	0.5	$\frac{14}{14+1}=\frac{14}{15}$	$\frac{3}{3+2}=\frac{3}{5}$
18	反类	0.48	$\frac{14}{14+1}=\frac{14}{15}$	$\frac{4}{4+1}=\frac{4}{5}$
19	正类	0.42	$\frac{15}{15+0}=\frac{15}{15}$	$\frac{4}{4+1}=\frac{4}{5}$
20	反类	0.2	$\frac{15}{15+0}=\frac{15}{15}$	1

数字表示转折点对应样本编号

ROC曲线下方面积为 $A U C$ , $A U C$ 值越大，表示分类模型的预测准确性越高， $ROC$ 曲线越光滑，一般表示过拟合现象较轻（为什么？？

2.各项指标的python实现，以logistic回归为例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, precision_score, recall_score, roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
plt.rcParams['font.sans-serif']=['STKaiTi'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
# 创建一个示例分类数据集
X, y = make_classification(n_samples=1000, n_features=20, random_state=42)# 将数据集分成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 训练一个分类模型，例如Logistic回归
model = LogisticRegression(random_state=42)
model.fit(X_train, y_train)# 在测试集上进行预测
y_pred = model.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'准确率 (Accuracy): {accuracy:.2f}')# 计算召回率
recall = recall_score(y_test, y_pred)
print(f'召回率 (Recall): {recall:.2f}')# 计算精确率
precision = precision_score(y_test, y_pred)
print(f'精确率 (Precision): {precision:.2f}')# 计算F1指标
F1 = 2*recall*precision/(recall+ precision)
print(f'F1={F1}')#ROC曲线和AUC值
fpr, tpr, thresholds = roc_curve(y_test, model.predict_proba(X_test)[:, 1])
roc_auc = auc(fpr, tpr)# 可视化ROC曲线
plt.figure(figsize=(10, 6),dpi = 300)
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC曲线 (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正率 (False Positive Rate)')
plt.ylabel('真正率 (True Positive Rate)')
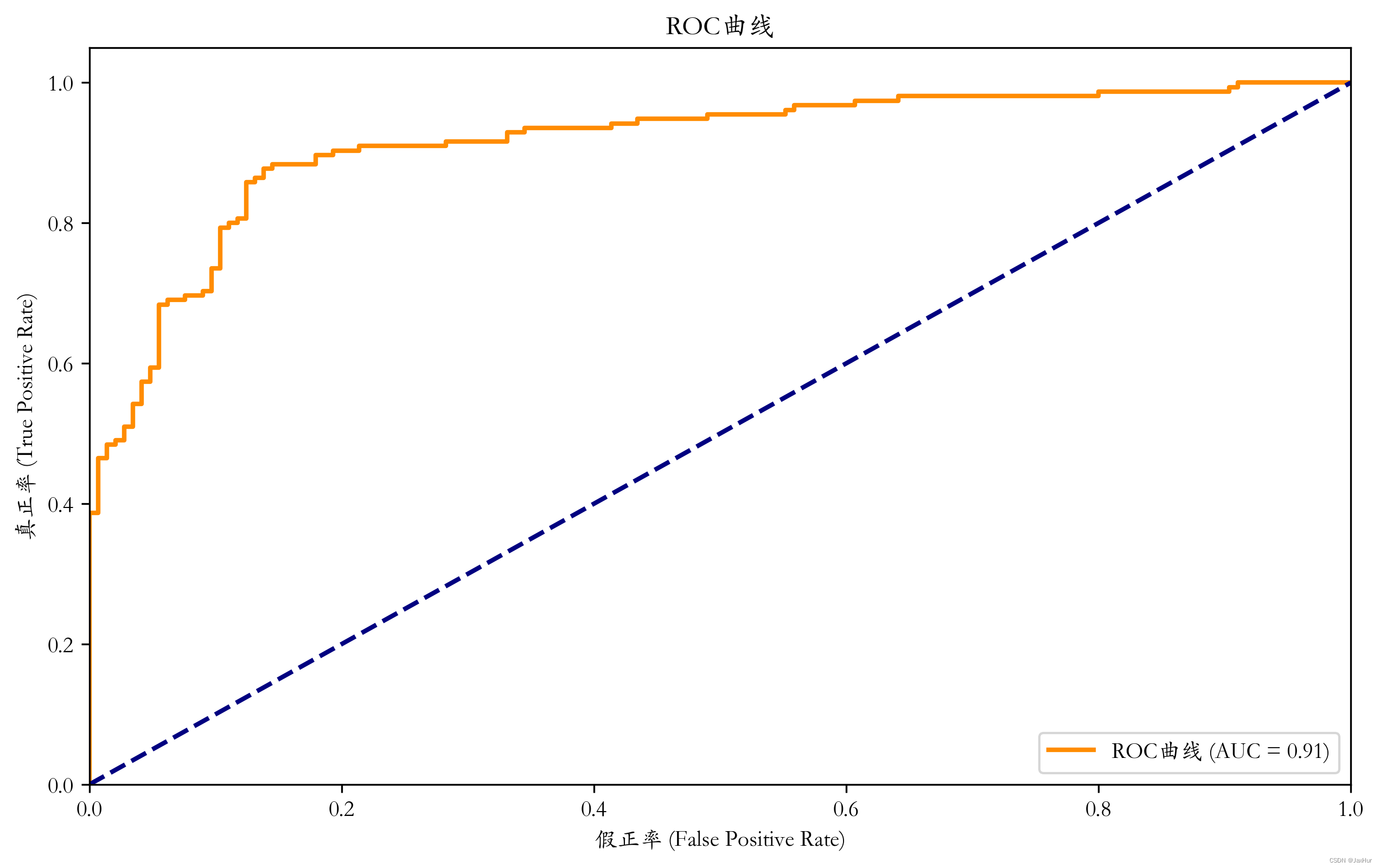
plt.title('ROC曲线')
plt.legend(loc='lower right')
plt.show()