一、RNN

1、场景引入

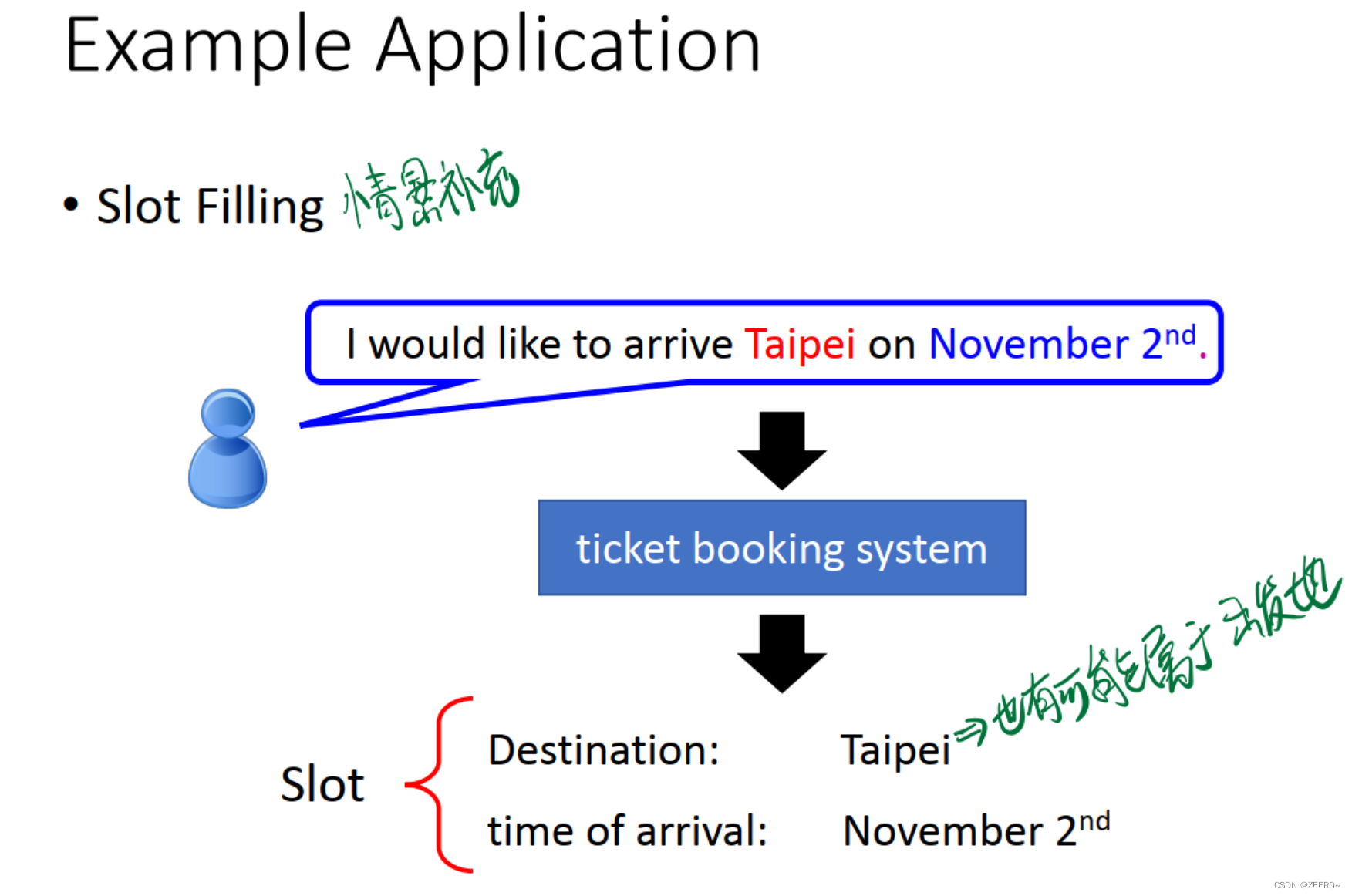
例如情景补充的情况，根据词汇预测该词汇所属的类别。这个时候的Taipi则属于目的地。但是，在订票系统中，Taipi也可能会属于出发地。到底属于目的地，还是出发地，如果不结合上下文，则很难做出判断。因此，使用传统的深度神经网络解决不了问题，必须引入RNN。

2、如何将一个单词表示成一个向量

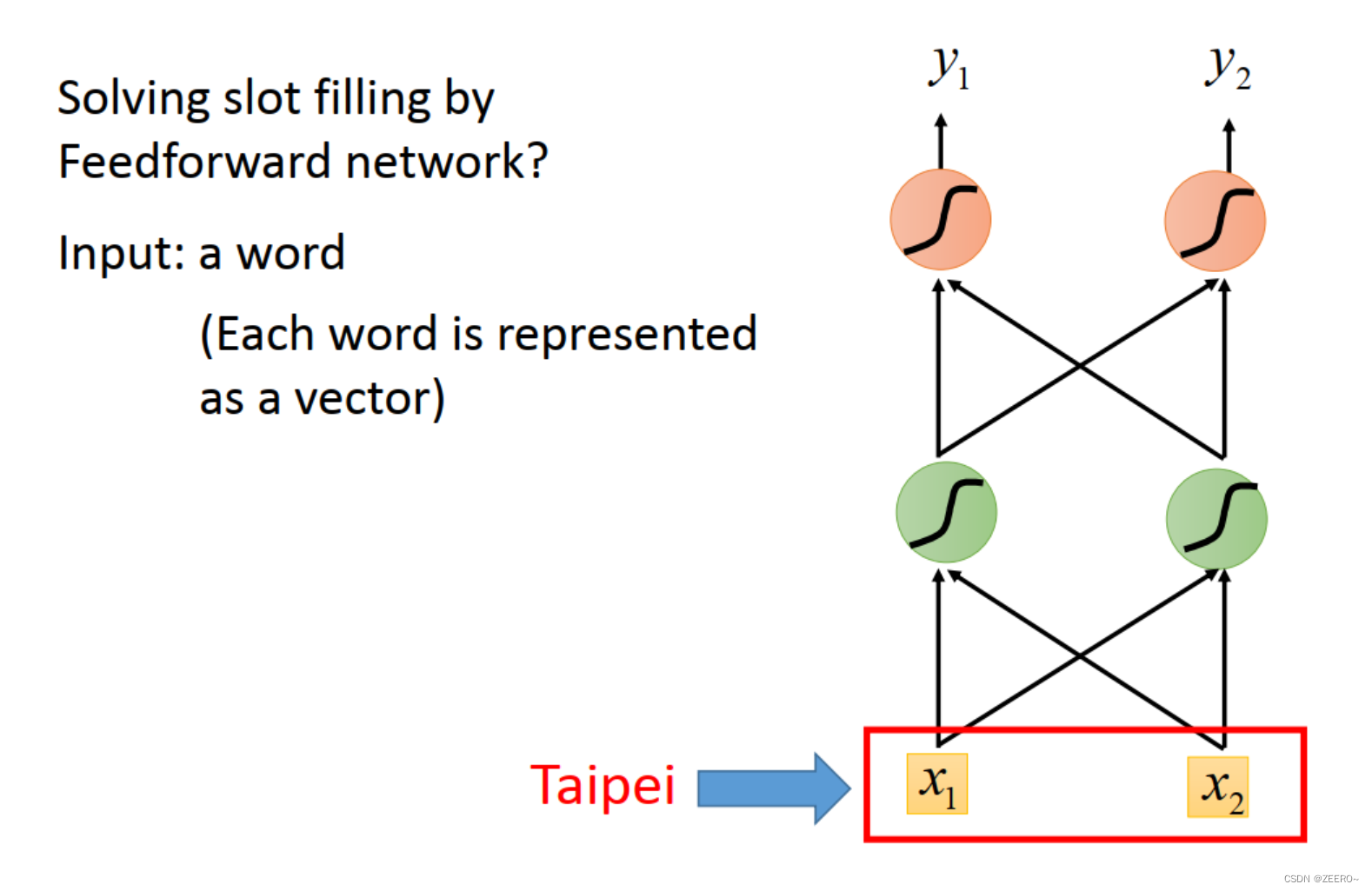
如上图所示，将词汇Taipi表示成[x1,x2]组成的向量。

一个最简单的方法是1-N encoding。思路是将所有的可能用到的词汇组成一个词典，然后假如我们一共只可能用到5个单词，则如上图所示，每个单词可以用1个五维向量来表示。

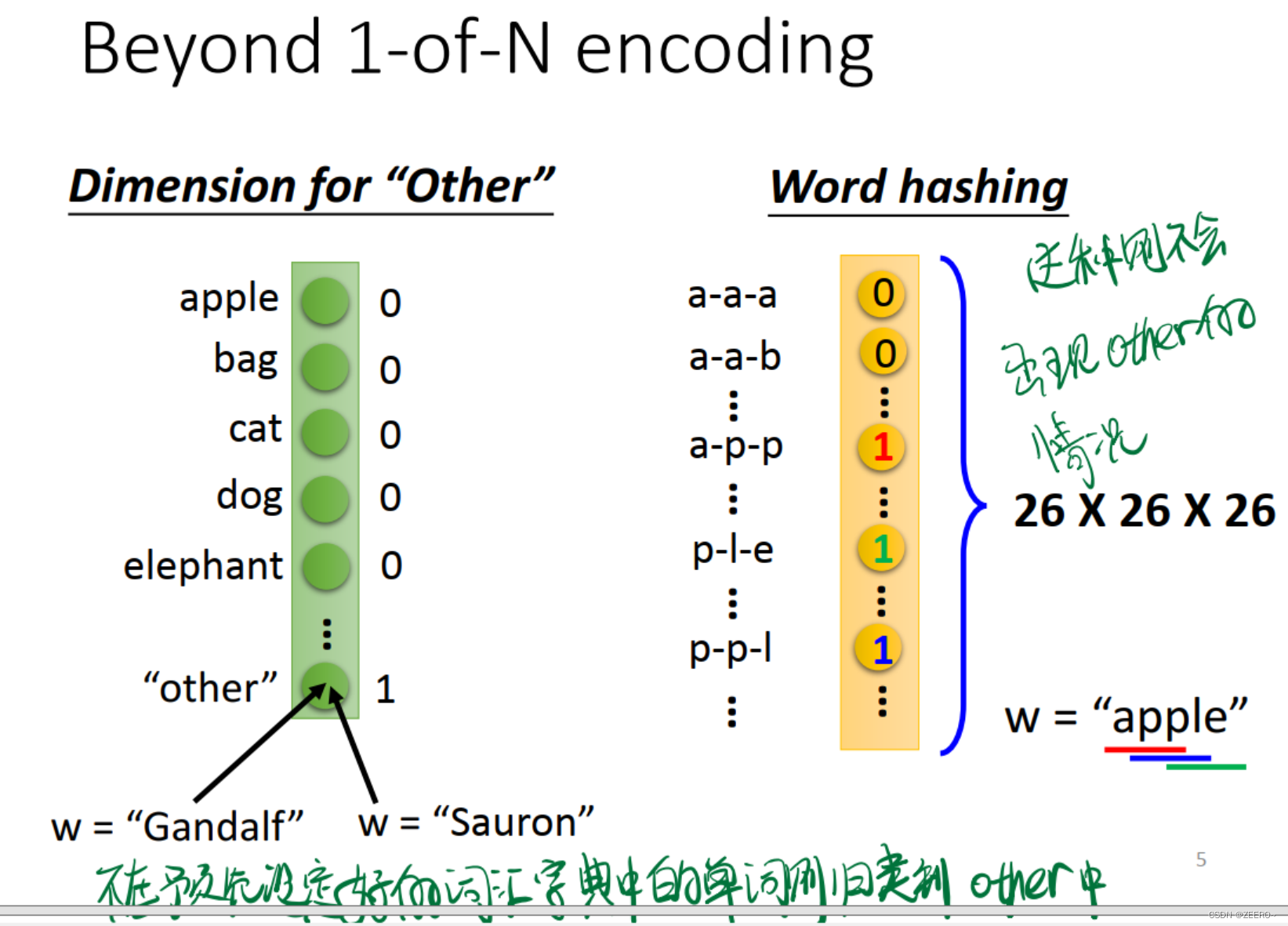
除了1-N econding之外，还有一些其他的方法。
第一种思路是设置1个other选项，将所有没有预先在词典中所设定的单词表示成other。
第二种思路是利用26个字母进行hash映射。这种情况下则不需要额外考虑other的情况。

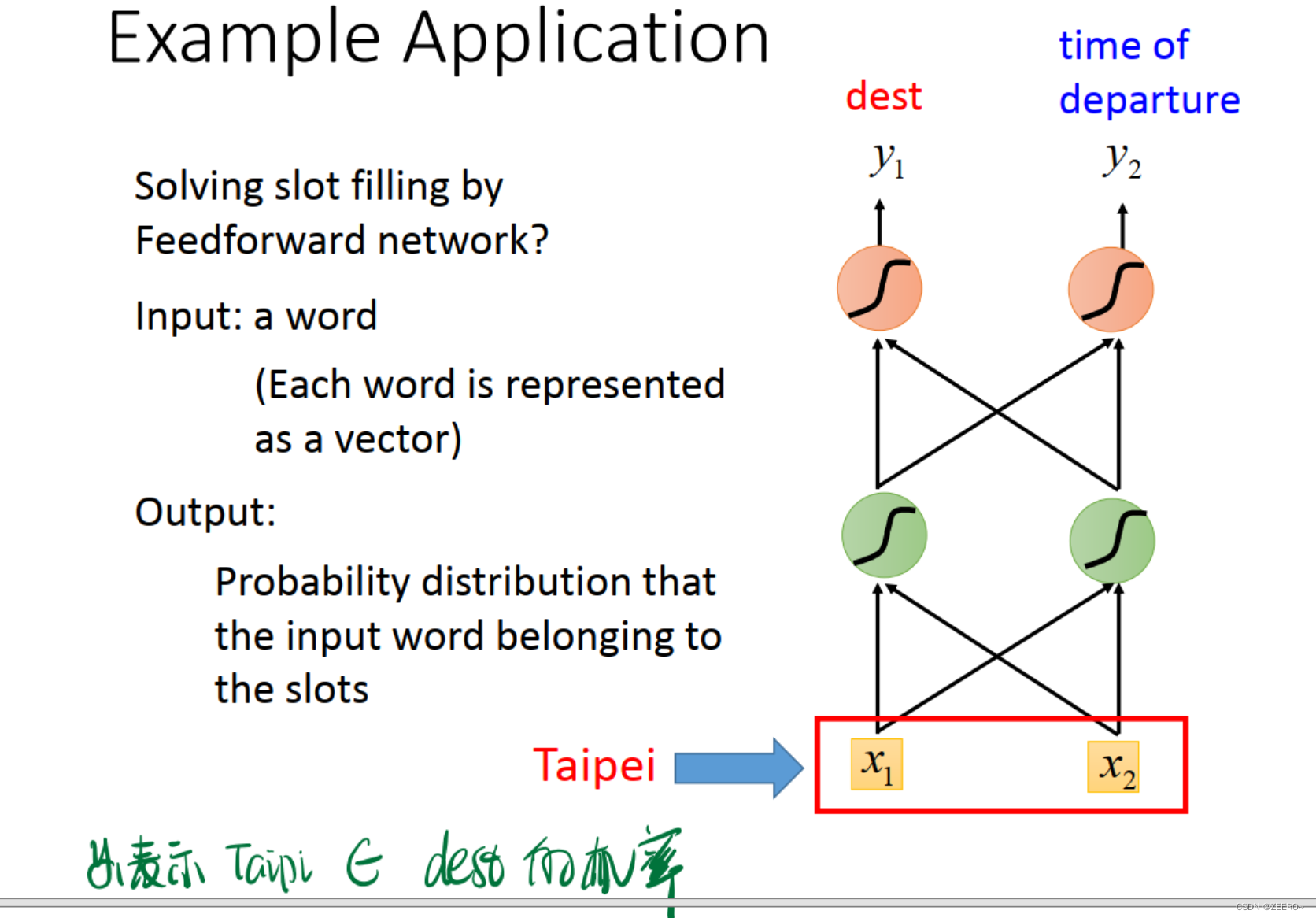
这样，将词汇向量化之后，我们指导，网络的输入为一个个的词汇向量，网络的输出则为：y1表示词汇属于dest目的地的概率，y2则表示词汇属于出发地的概率。最后其实应该还有一层，做出预测，属于哪个概率最大，则输出哪个。

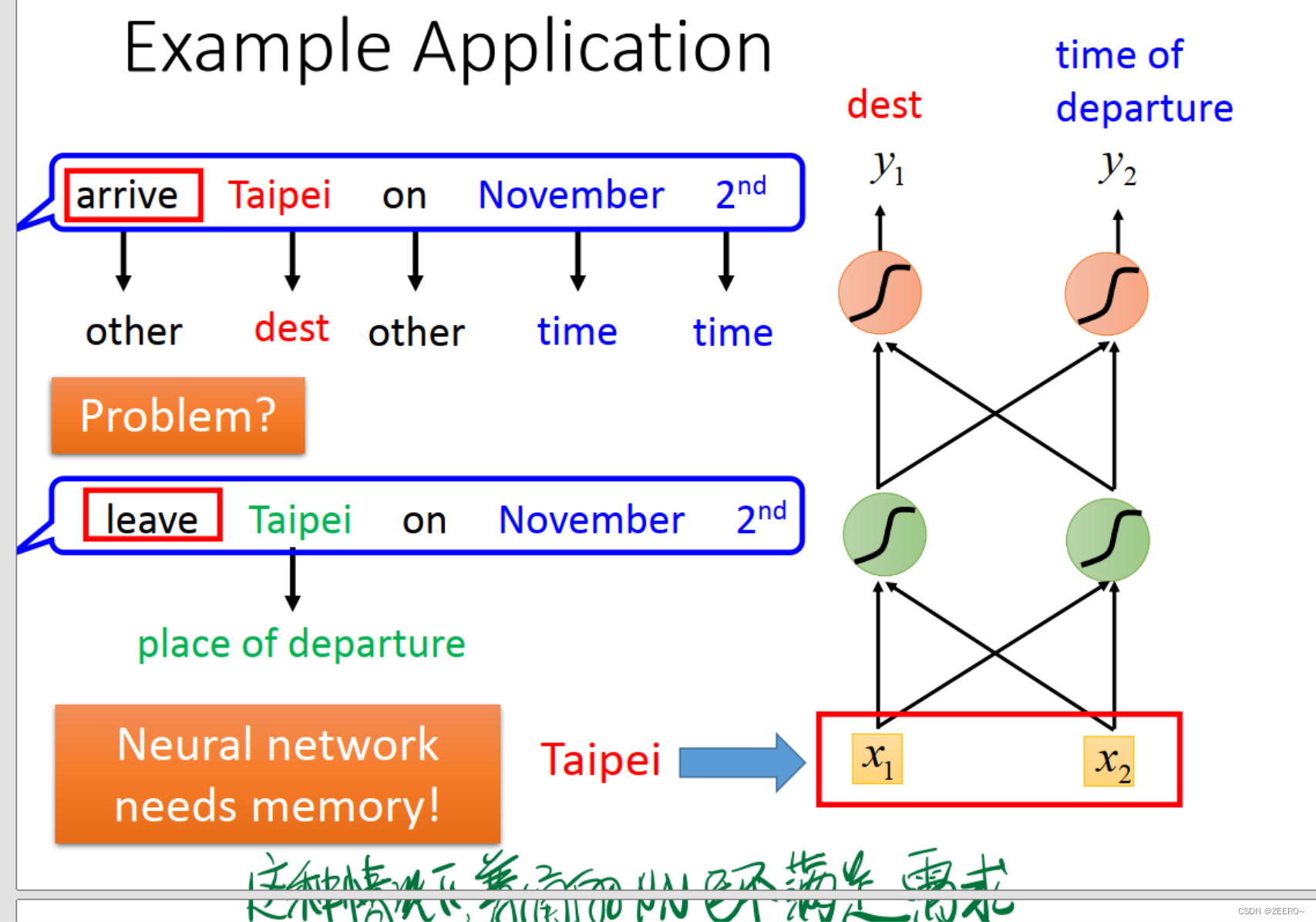
这个时候，我们所构建的NN则是需要有记忆的，否则无法解决该问题。

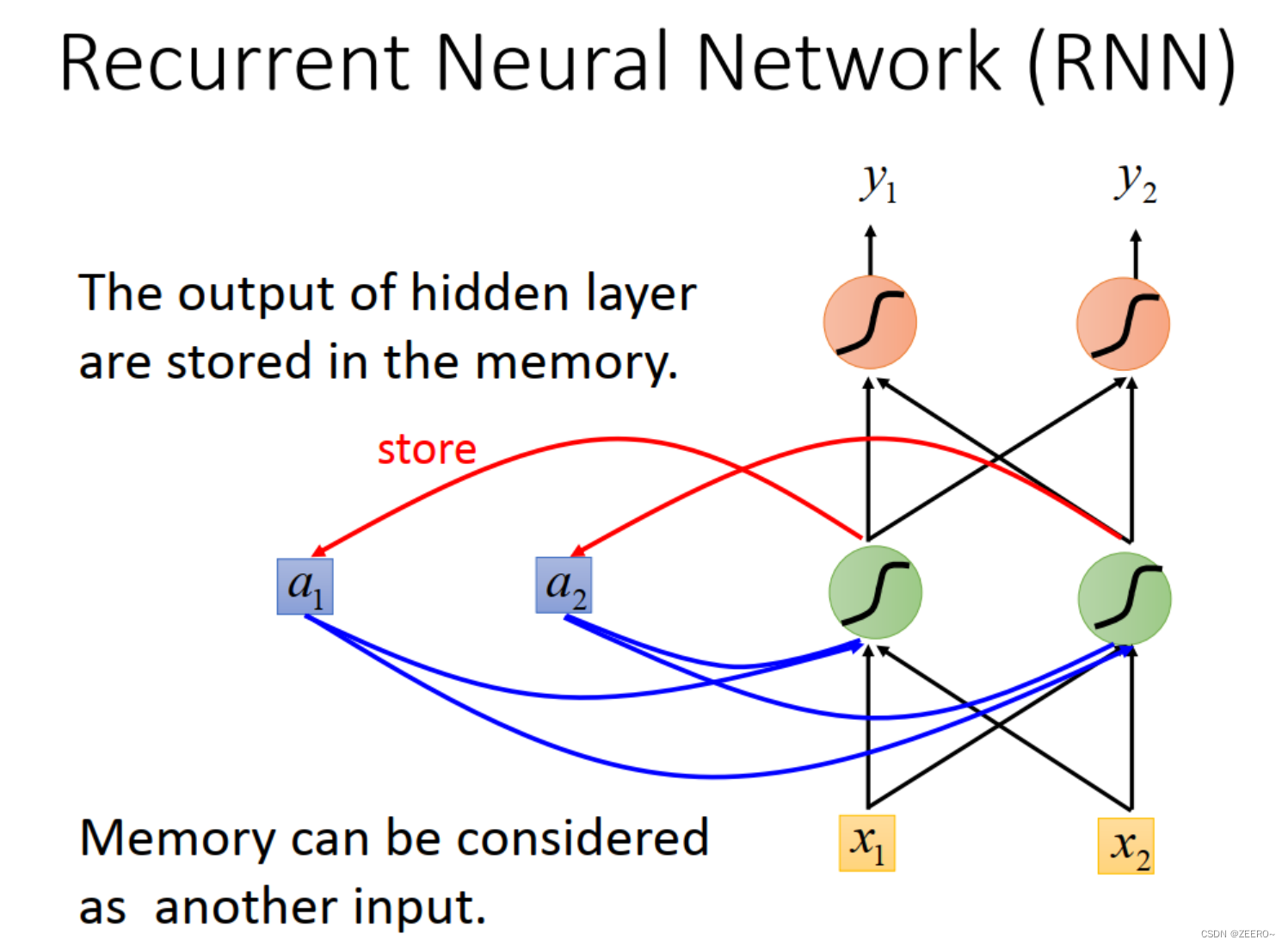
因此，我们引入了RNN来解决该问题。将每次hidden layer的输出先储存到memory cell中，作为下个词汇向量的输入。不断循环该过程。

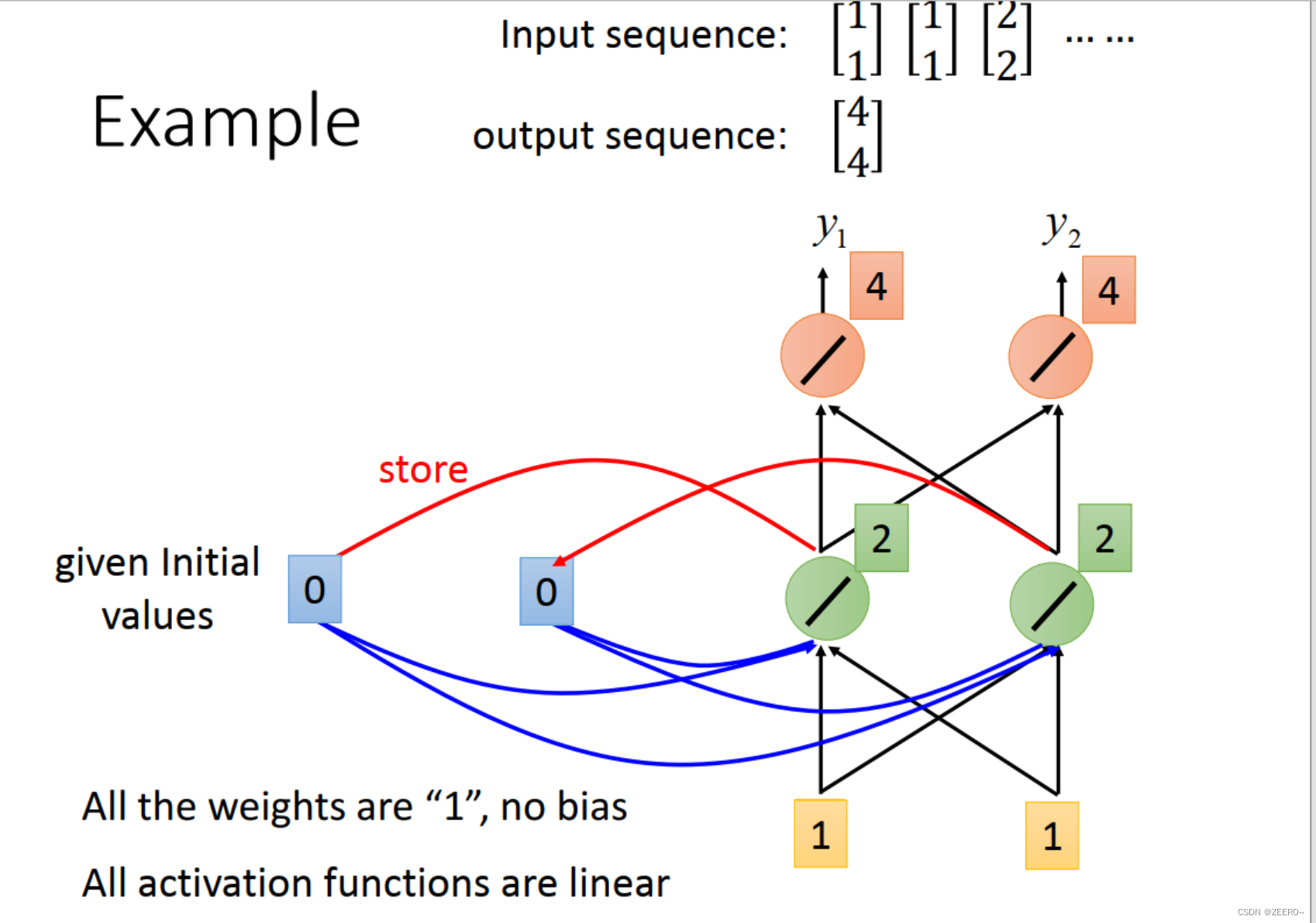
举例来说，我们输入的第一个向量为[1,1]，则hidden layer的输出为[2,2]，先被储存起来，输出为[4,4]。

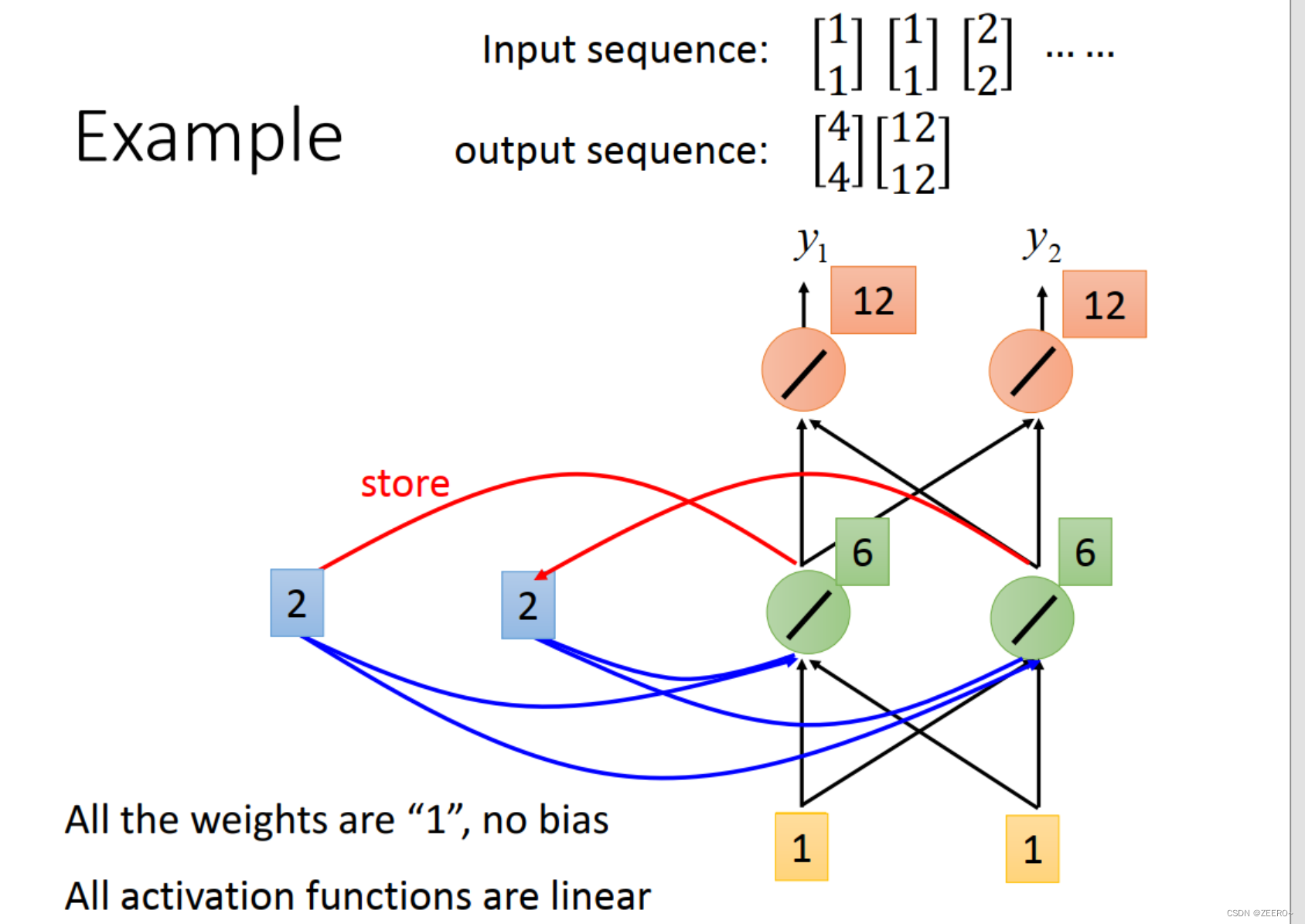
第2个输入仍然为[1,1]。这个时候结合前一个memory的输出[2,2]，hdden layer的输出为[6,6]，output为[12,12]。

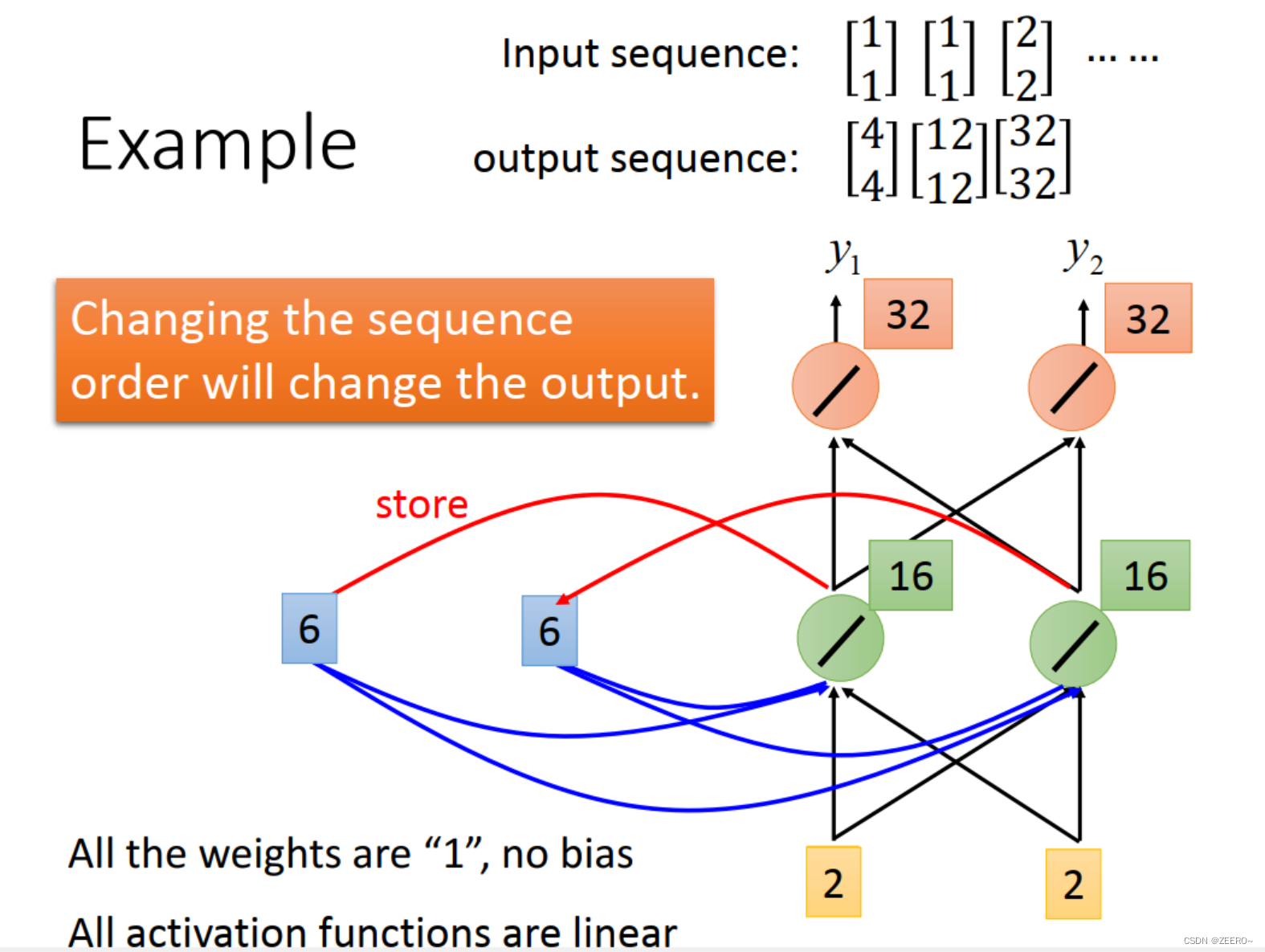
第3个输入为[2,2]，结合前一个memory的输入为[6,6]，这个时候hidden layer的输出为[16,16]，output为[32,32]。

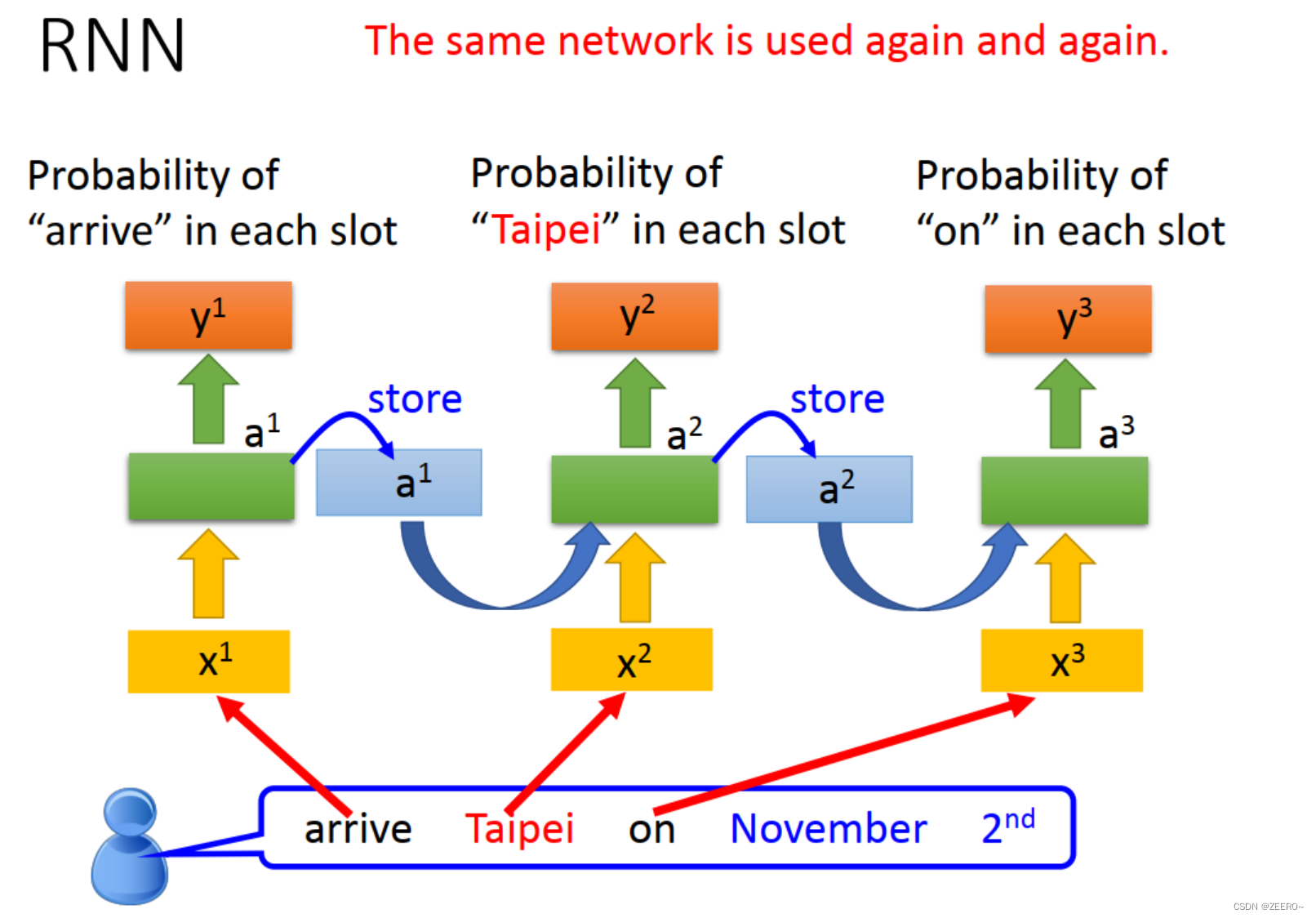
RNN的网络结构如上图所示，重复利用了同一种相同的网络结构。

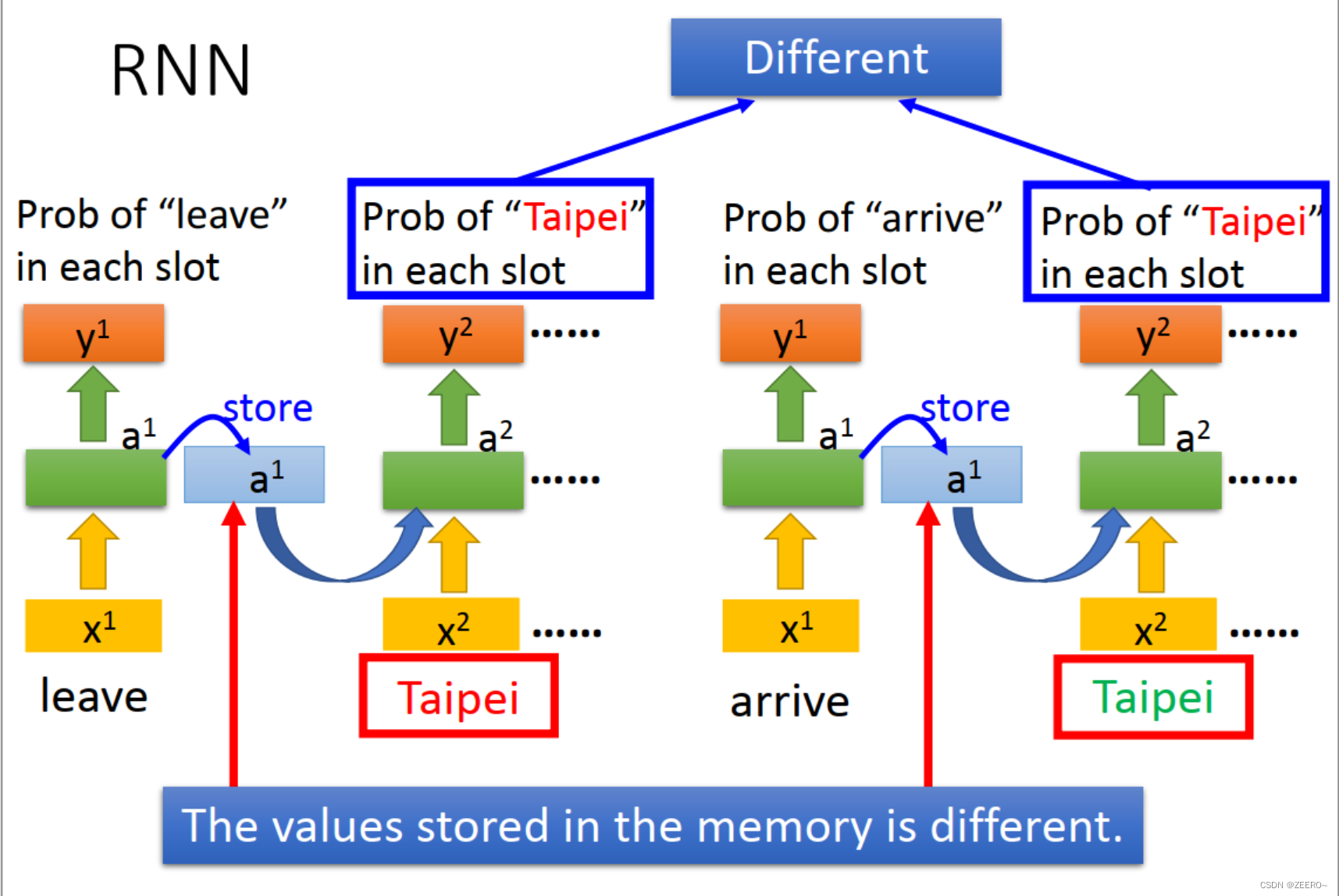
每次储存在memory中的值并不相同。

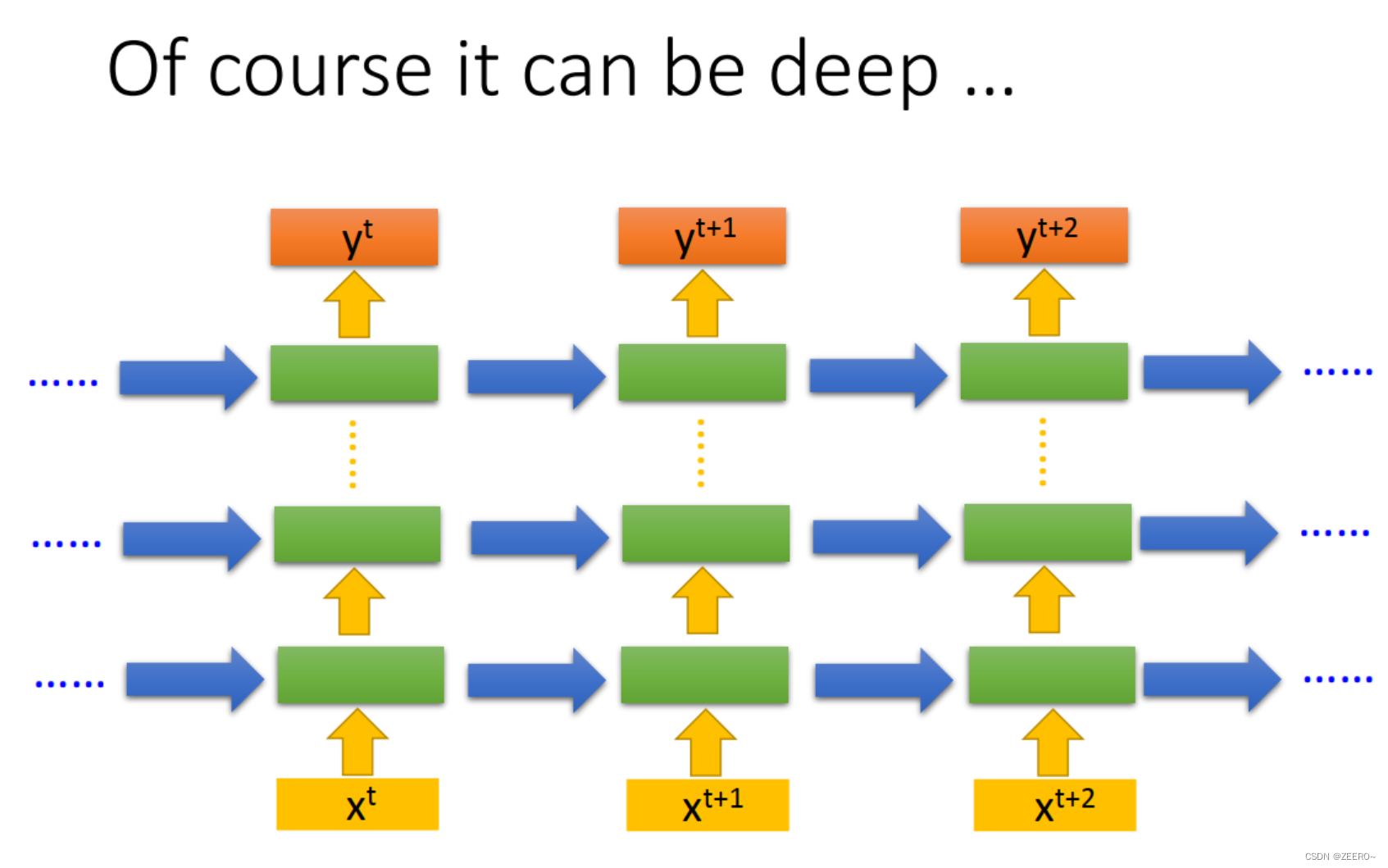
当然，也可以把hidden layer的层数加深。

3种典型的RNN网络结构

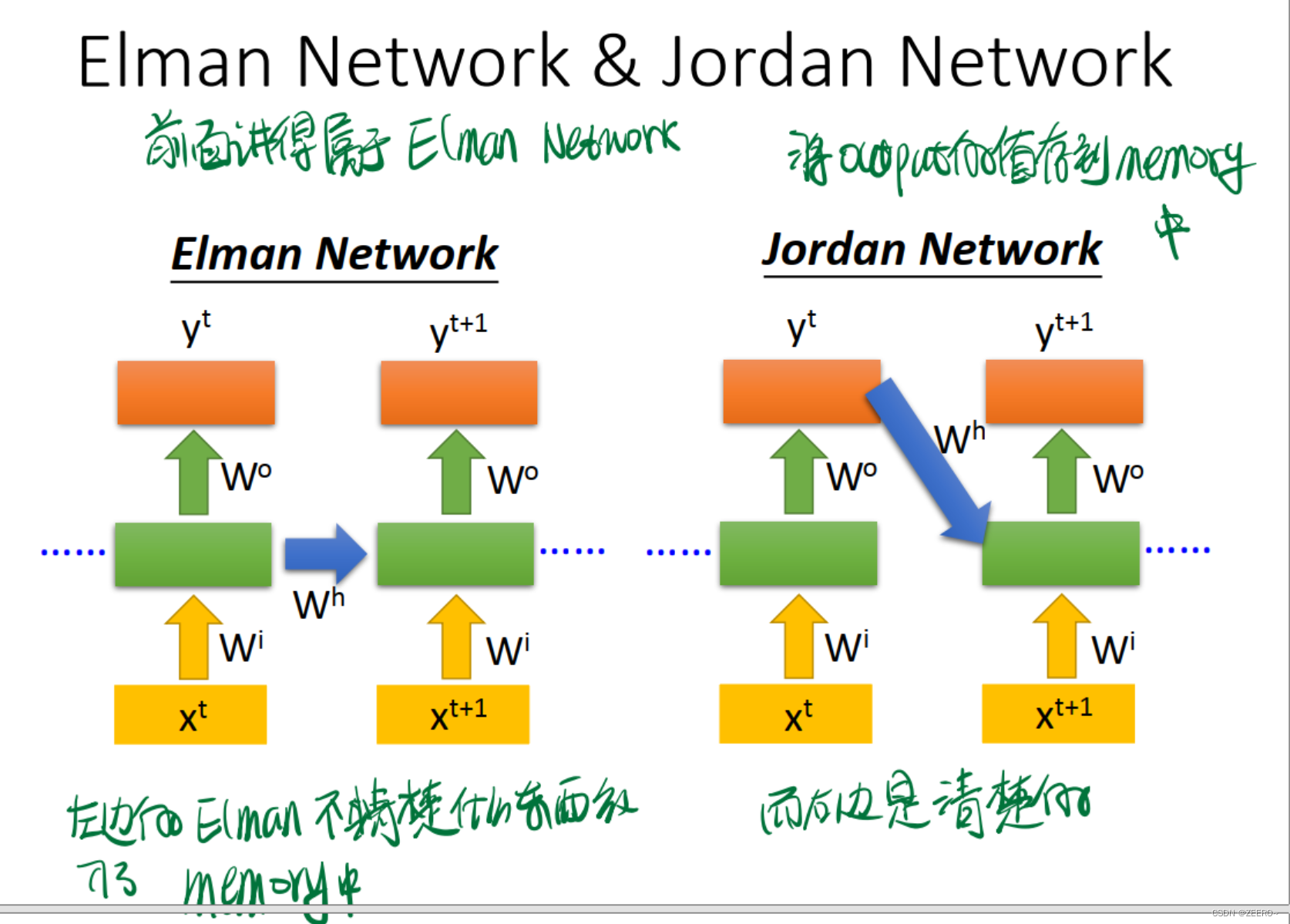
Jordan Network和Elamn Network的区别在于是将每个output的值作为下一个的输入。右侧的网络结构可解释性更强。

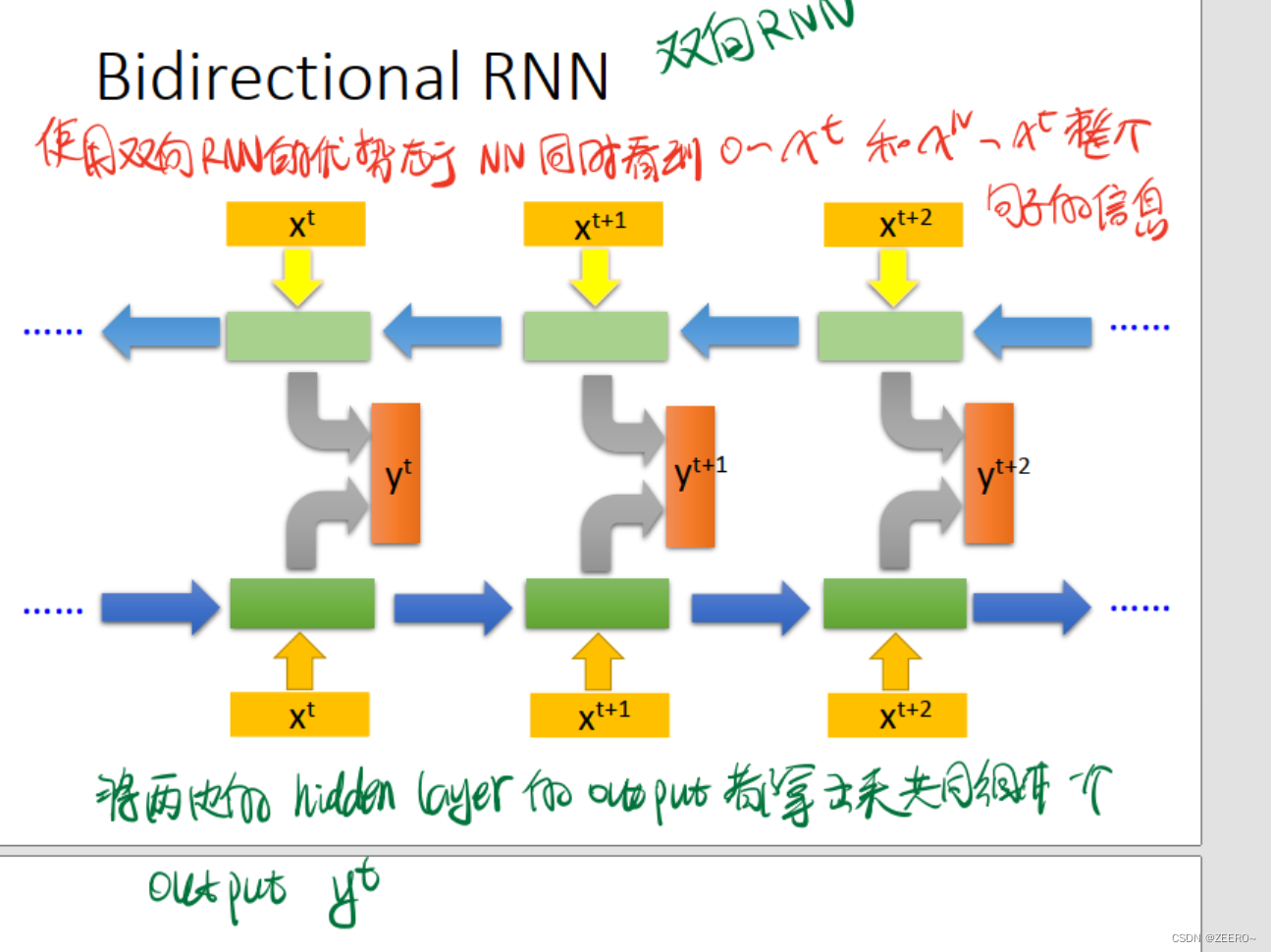
双向RNN则更为全面，同时兼顾到了前后的上下文信息，而不仅仅是前面的信息。

二、LSTM

我们在实际过程中使用更多的则是LSTM。

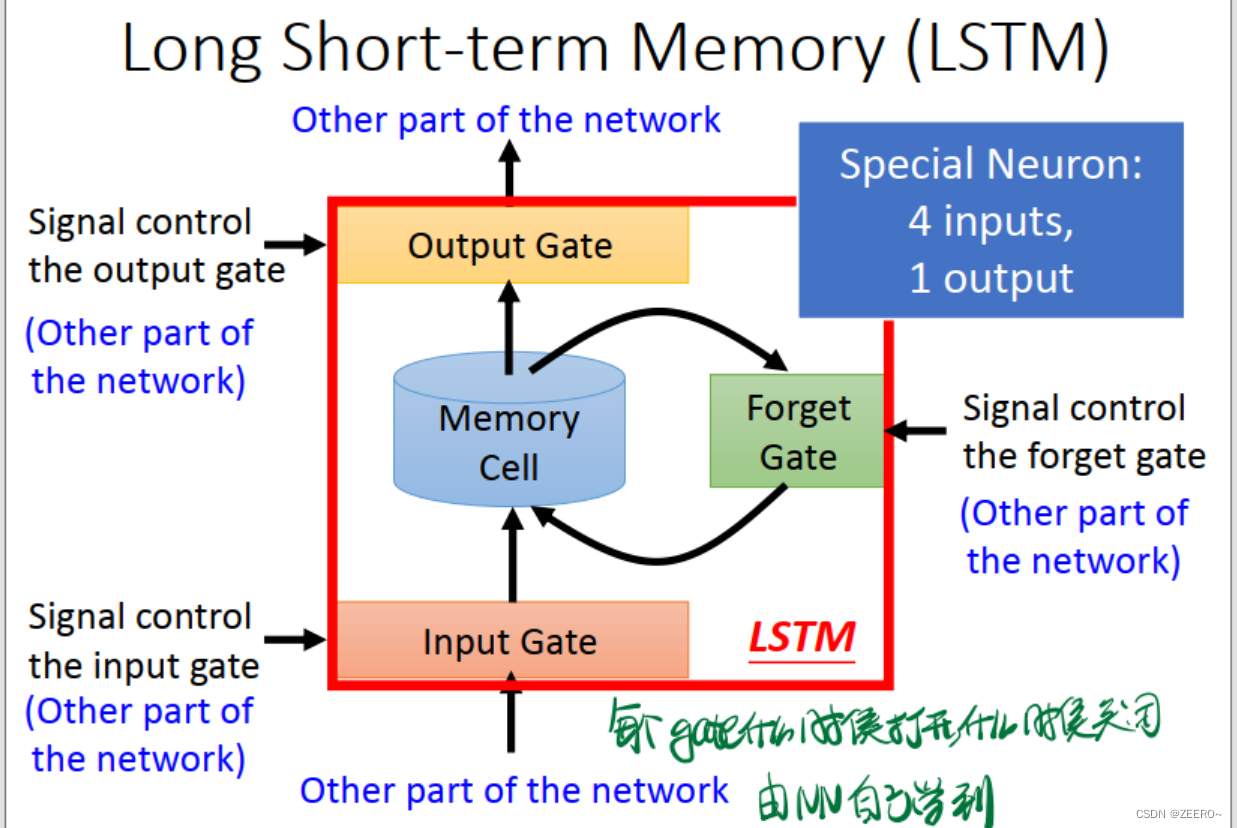
LSTM实际上，是将RNN中hidden layer的输出存入memory cell的过程稍微复杂化了一些，使用了3个gate进行代替。input gate的作用是控制输入通过，forget gate的作用是控制对memory cell中的值是否进行清空。output gate的作用是控制是否将该memory cell的值输出。

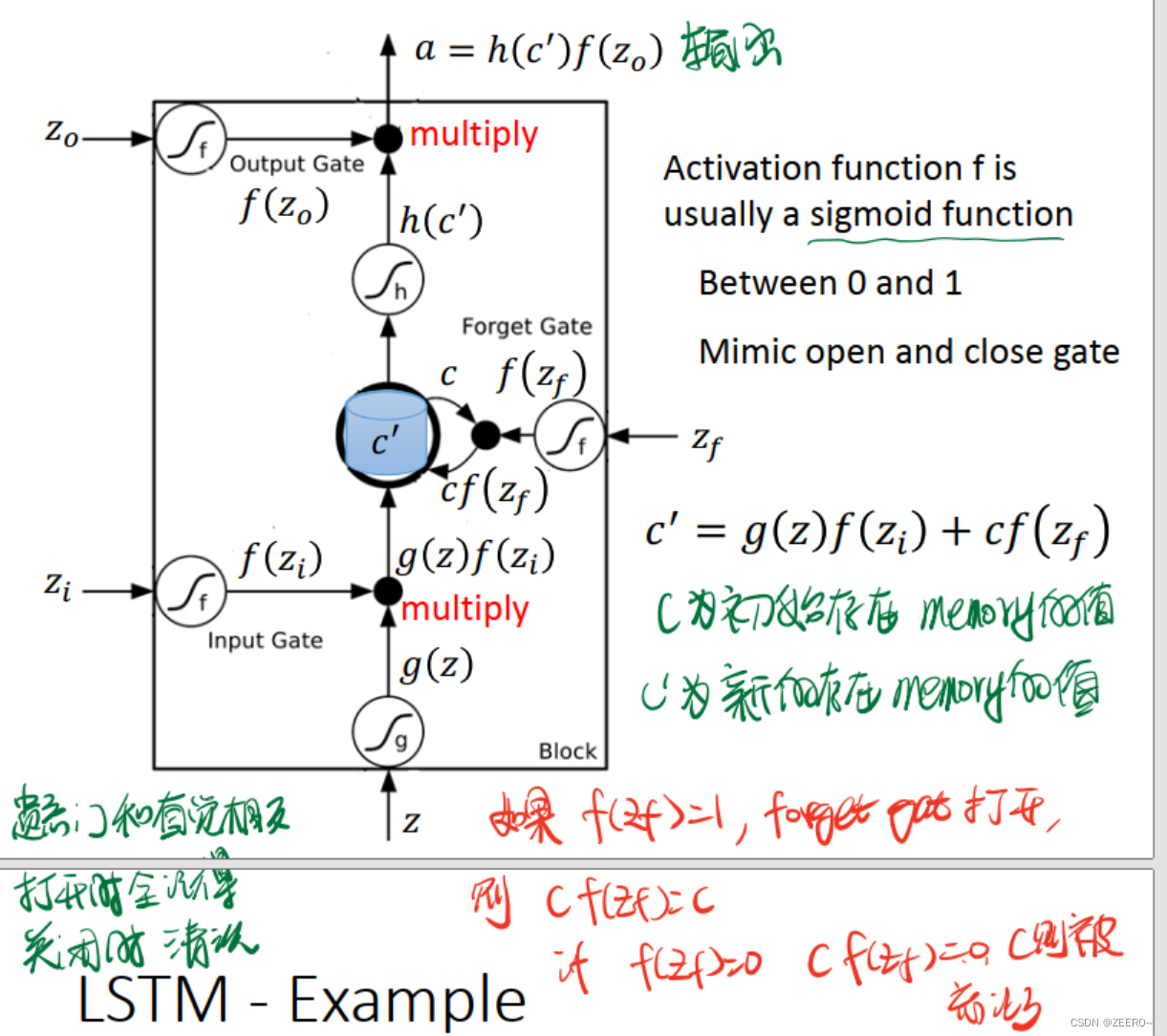
每个门的激活函数都是sigmoid函数，因为这样恰好可以将输入值映射到(0,1)之间。0表示不允许通过，1表示可以通过。
这里额外说下，forget gate和直觉似乎有点相反。当$f(z_f)=1$时，表示forget gate打开，但是$cf(z_f)=1$，c表示前一个memory cell的值,$c^{\prime }$表示本次计算出来的值。这个时候，前一次计算出来的c的信息完全没有被forget。因此，forget gate打开时，不是表示forget，而是表示unforget。

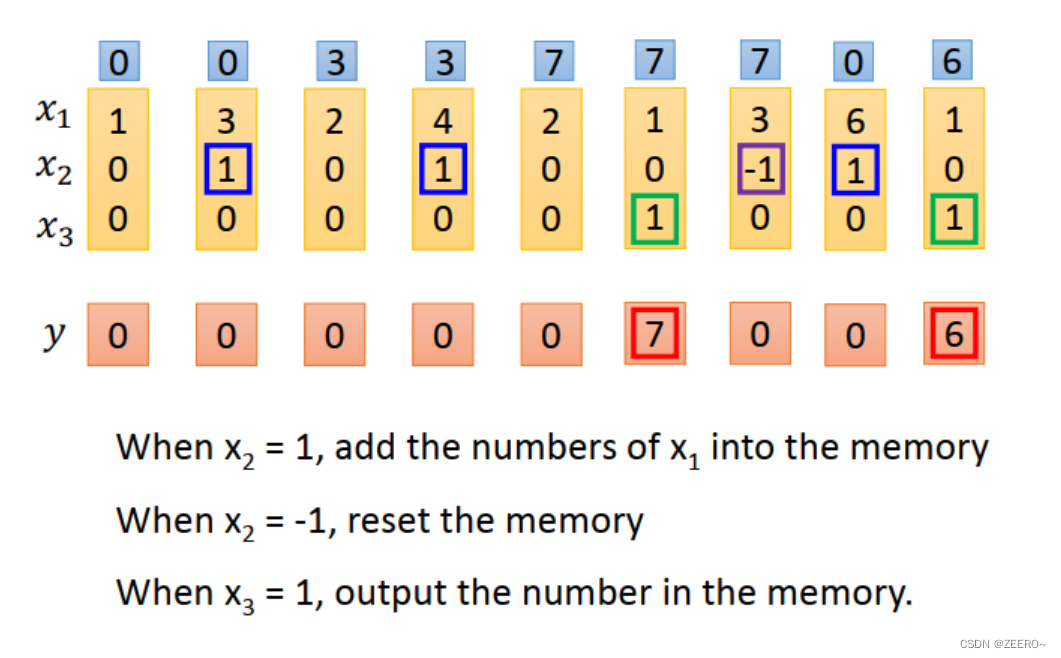
举例来说，假如想设计一个LSTM网络，实现上面的功能。
当x2=1时，将x2的值写入到memory中。memory时最上面蓝色框的值。
当x2=-1时，将memory中的值进行reset。
当x3=1时，将memory中的值进行输出。

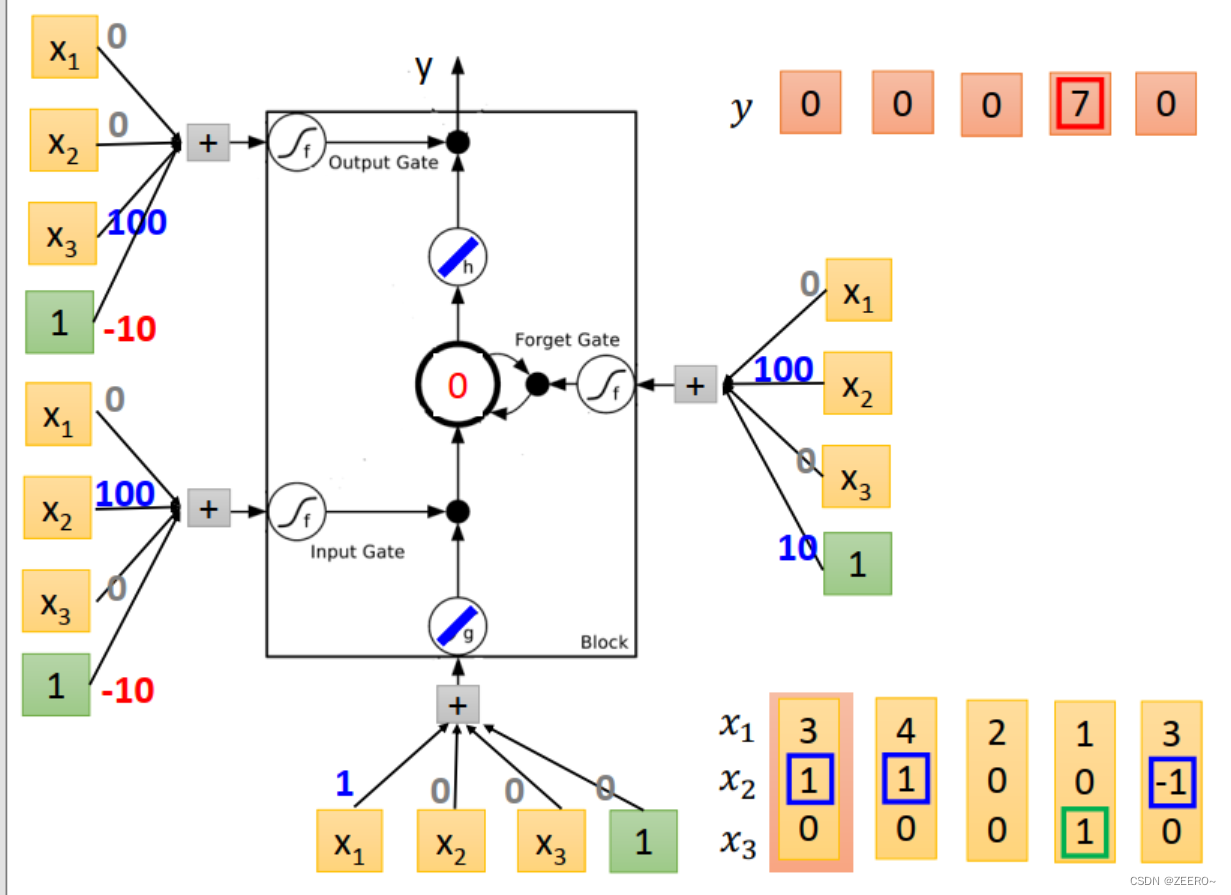
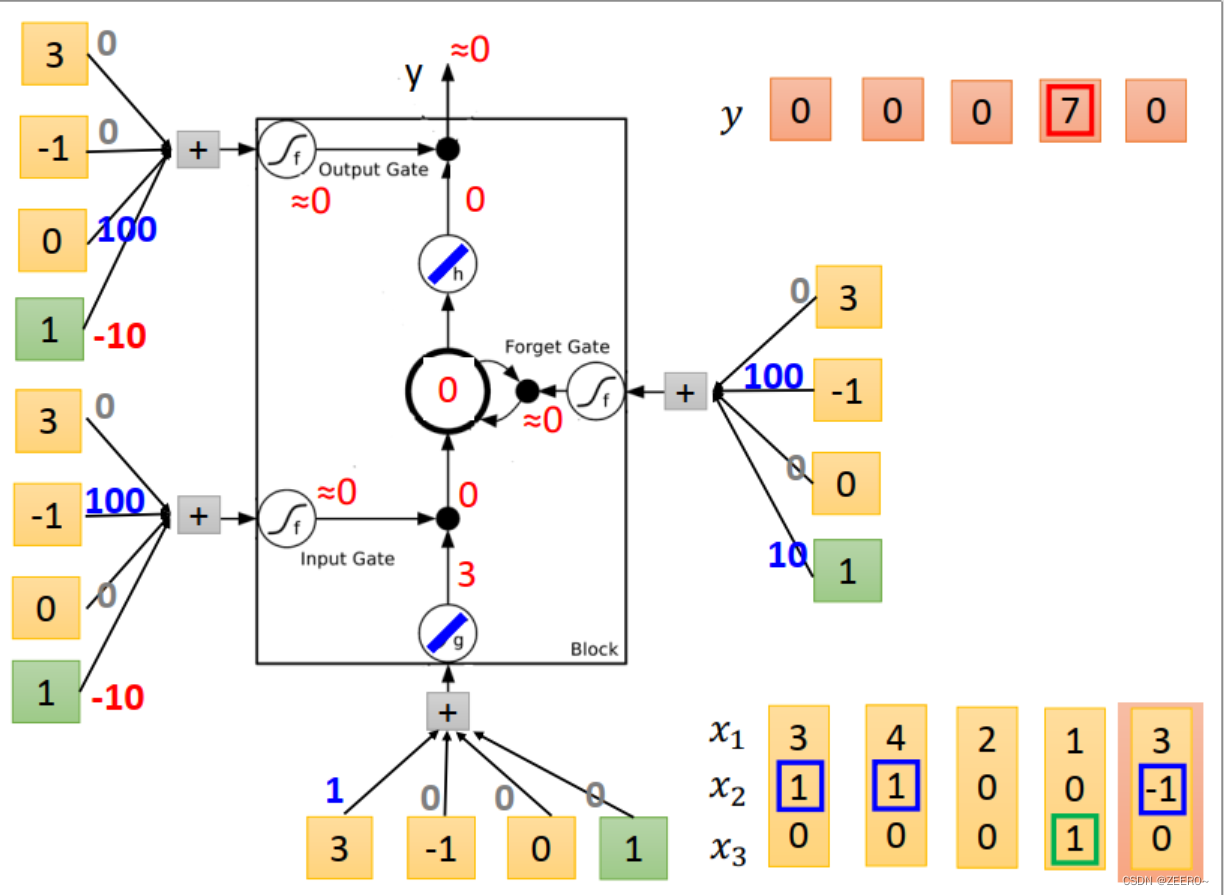
我们设计的NN结构如上图所示。输入乘的4个weight为[1,0,0,0]。input gate控制信号为输入与[0,100,0,-10]相乘，依次类推。

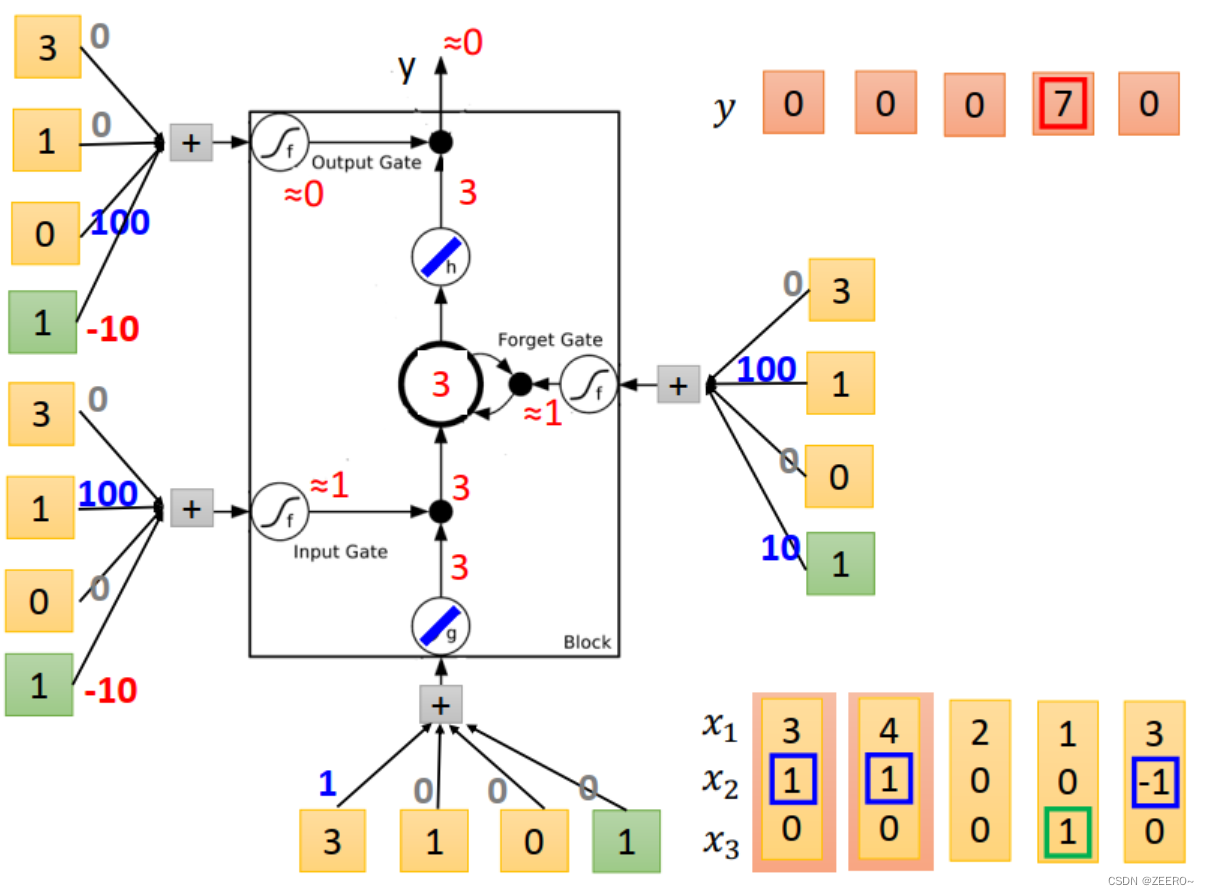
当输入为[3,1,0]时，input的值为3，input gate的值为1，multiply之后得到3.forget gate 的值为1，与前一个memory cell的值0相乘后再加3得到3，outputgate 的值为0，因此输出为0，memory cell的值更新为3，为本次运算的结果。

当输入为[4,1,0]时，input 的值为4，input gate=1，multiply之后得到4，forgat gate =1，与$C_{t-1}=3$相乘后+4=7，forget gate的值为0，因此output=0，memory cell更新为7.

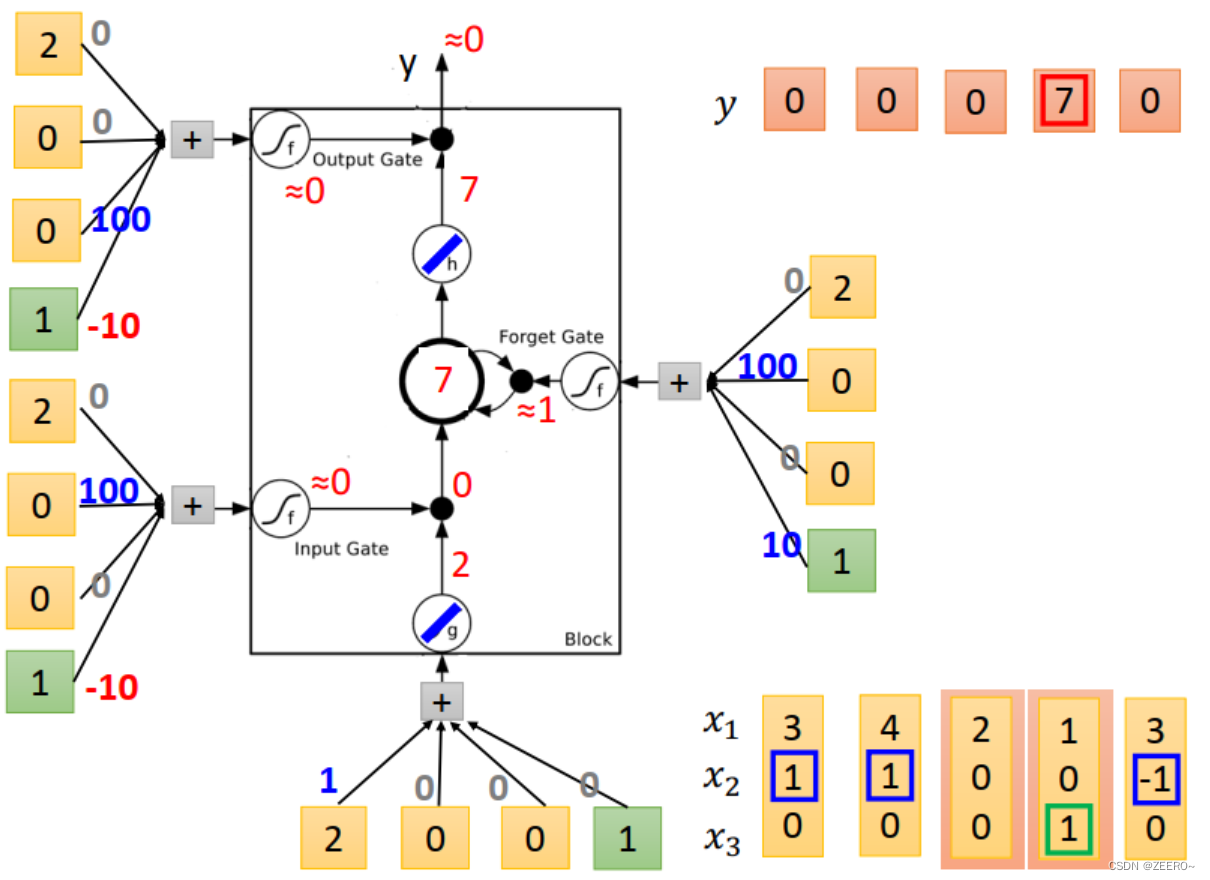
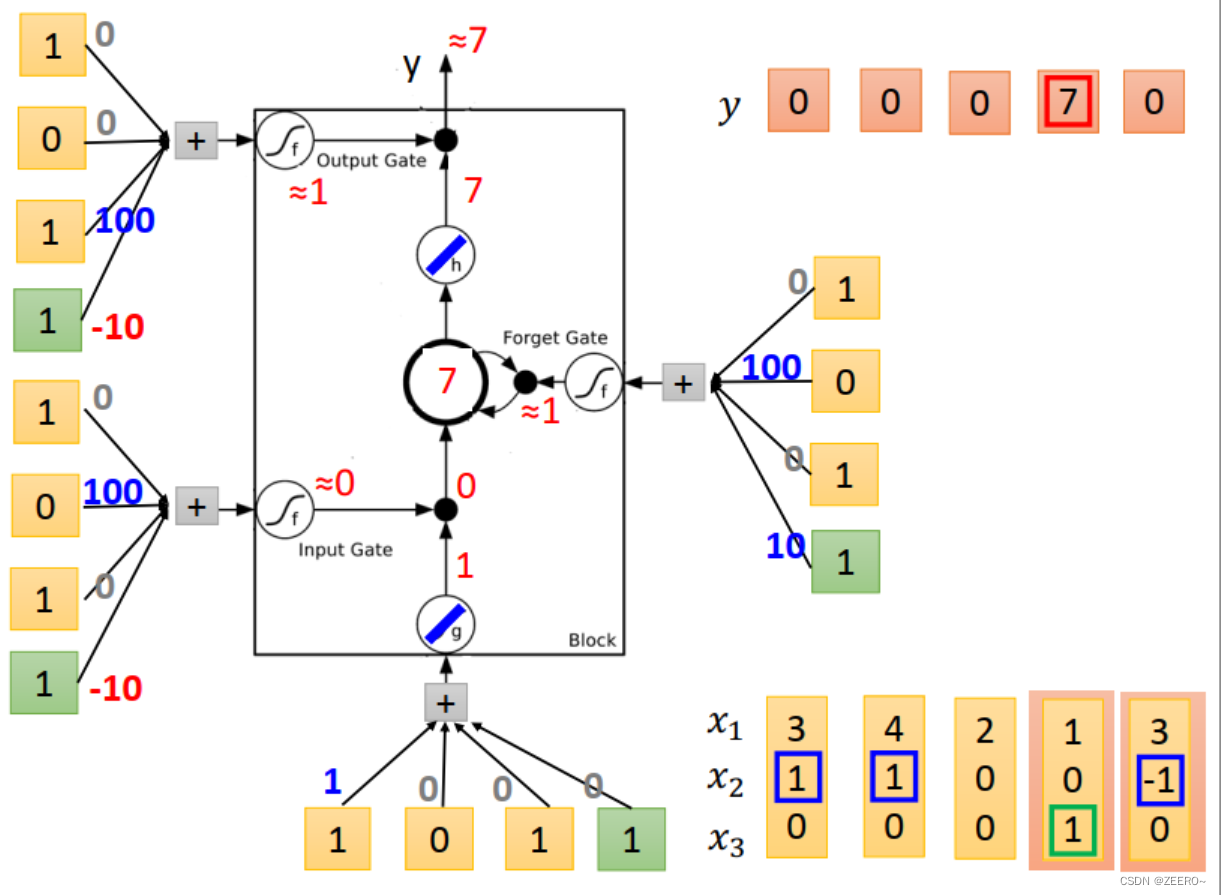
LSTM和普通NN、RNN区别

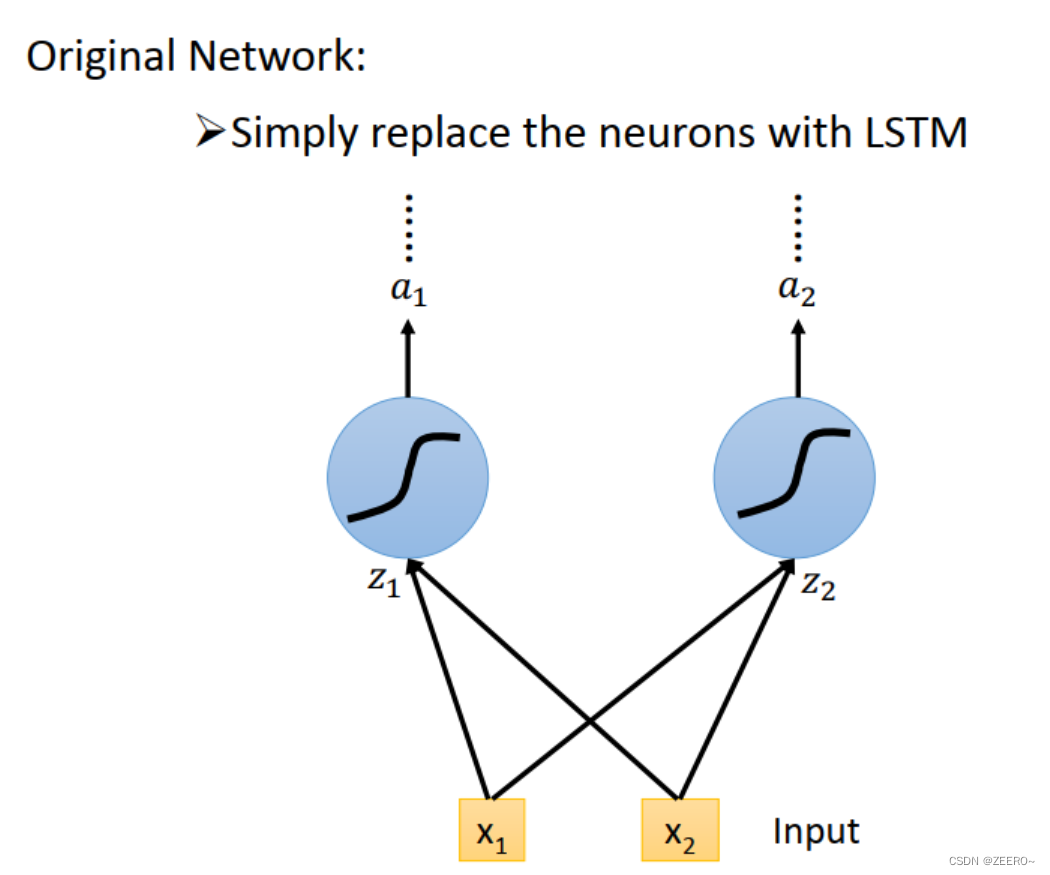
前面已经讲述过，LSTM可以看作是将普通的hidden layer替代成由4个输入控制的cell。

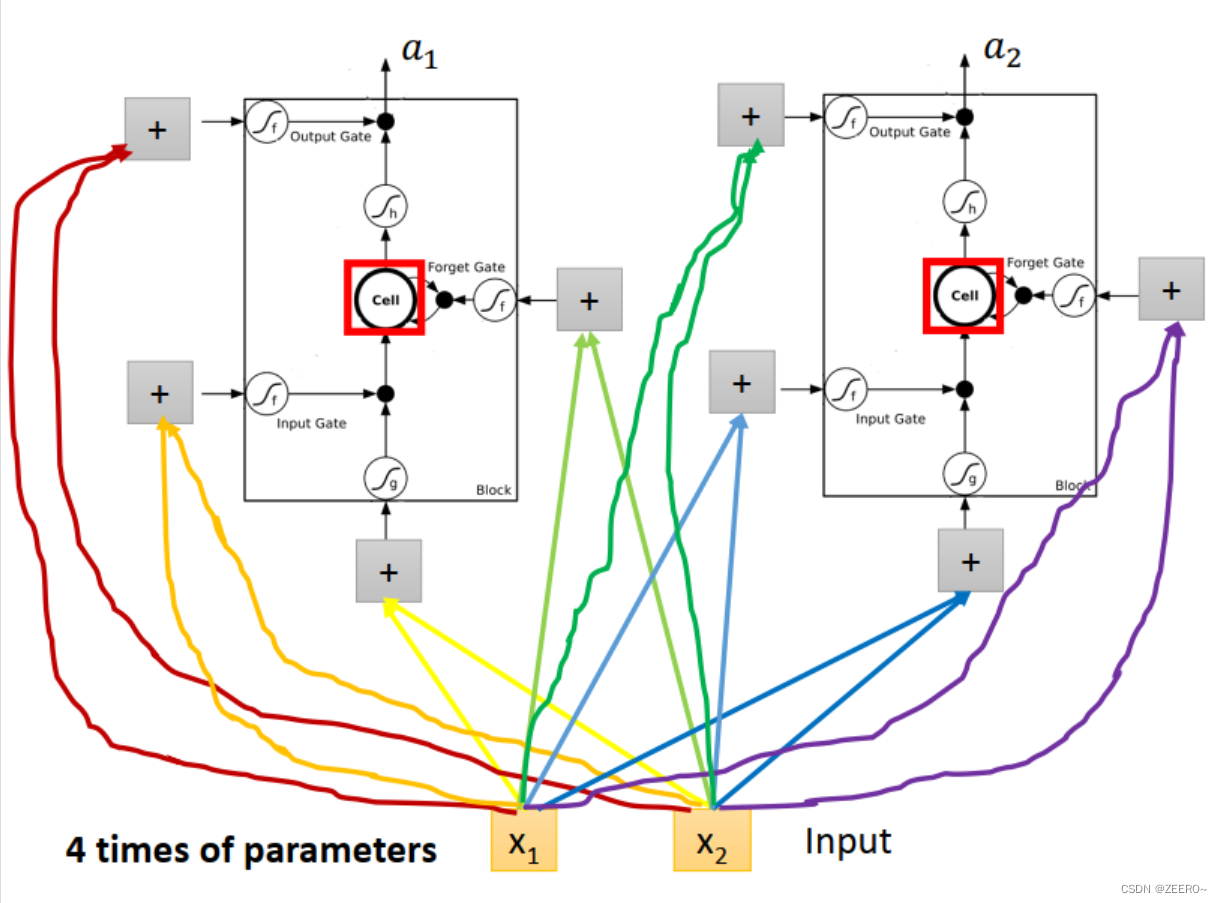
将输入[x1,x2]分别乘上不同的matrix后输入，用于控制input ,input gate,forget gate,output gate。因此，LSTM网络结构的参数量是普通NN的4倍。



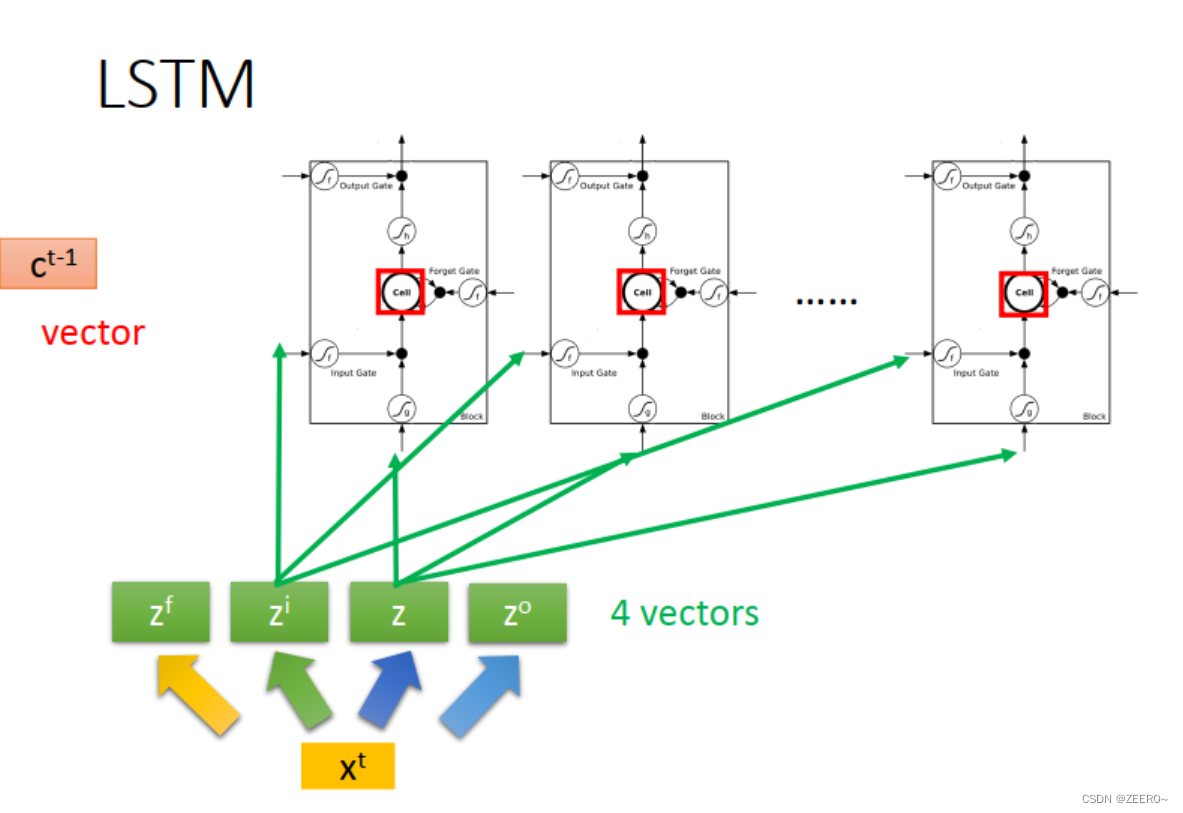
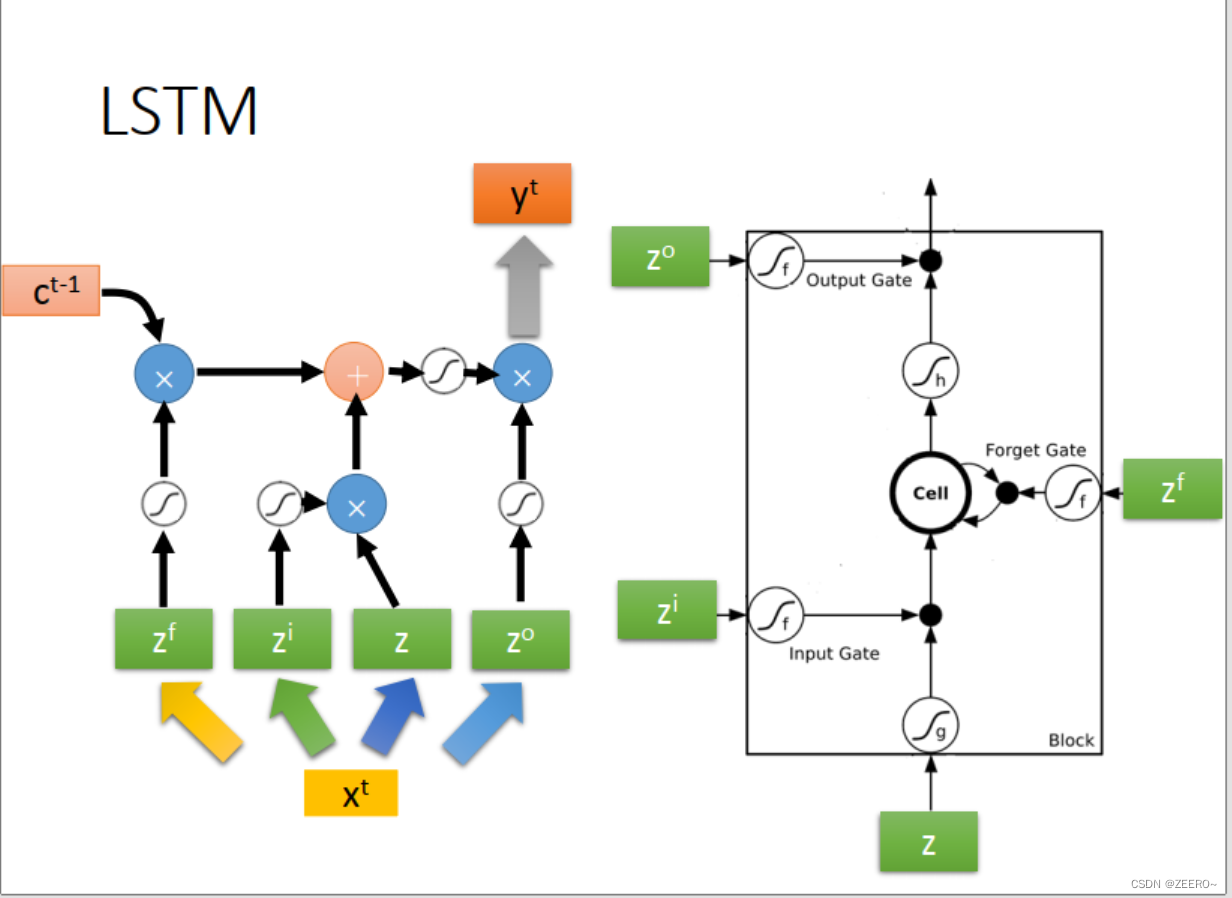
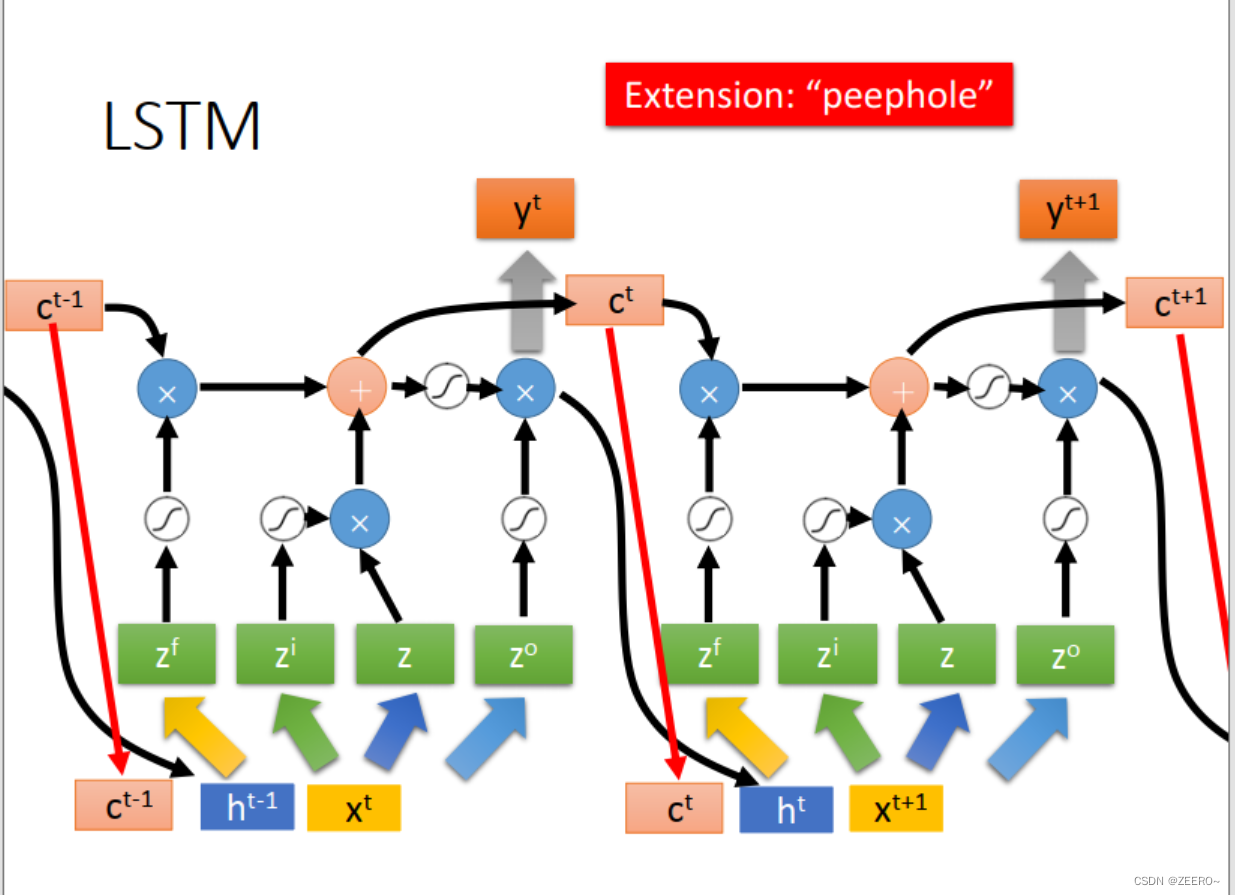
这里,peephole，指的是，在实际LSTM网络结构设计中，会将前一时刻的memory cell的值ct，输出ht的值一并加入到下一时刻作为输入。

这里LSTM虽然看起来很复杂，但是在实际中往往这是最标准化的设计。我们可以借助工具来实现它。

三、 RNN的训练

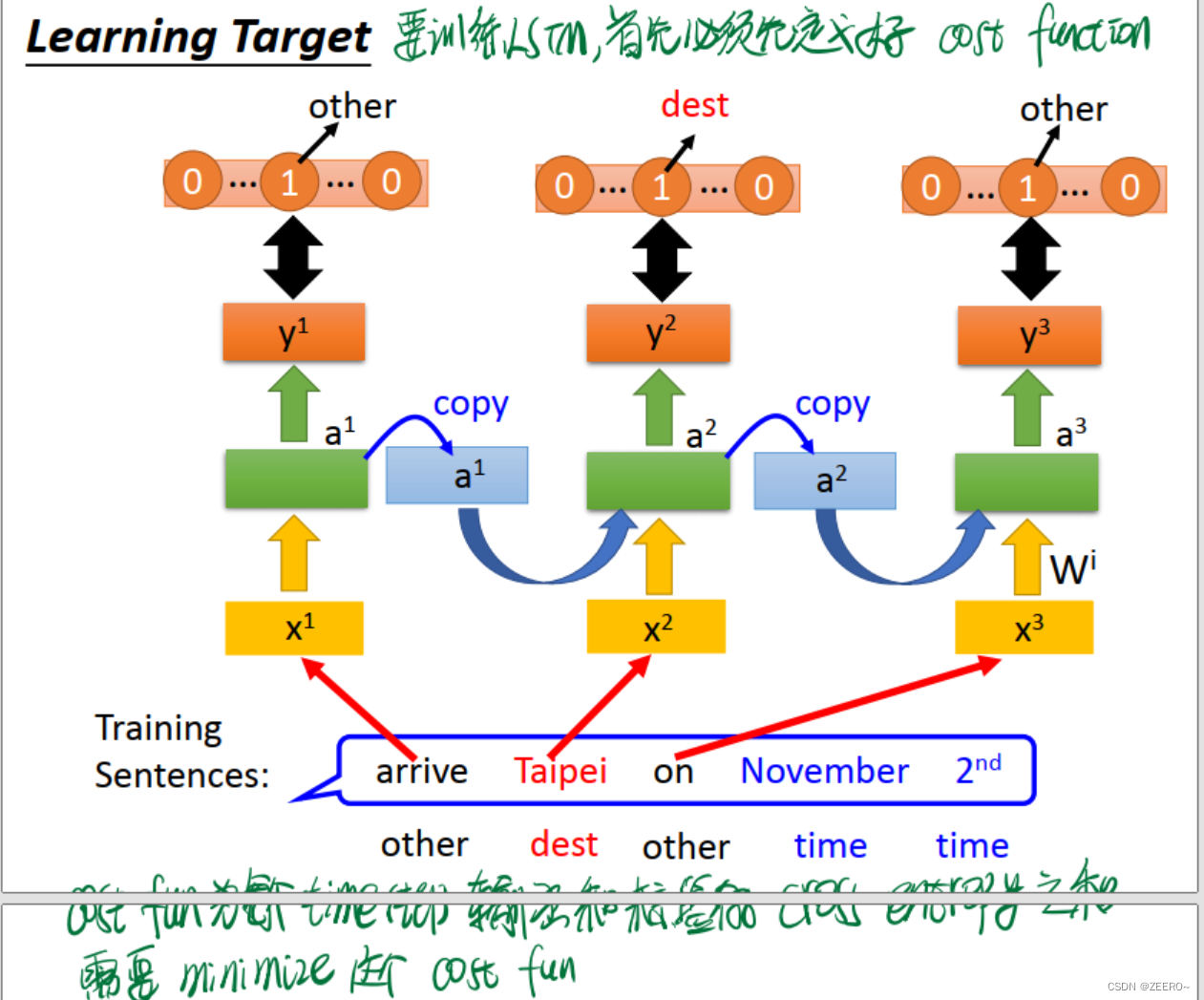
如果需要train一个RNN，则必须首先定义好cost function。很显然，这里RNN的cost function为每个time step的输出和对应标签vector的cross entropy之和，也是我们需要minimize的函数。

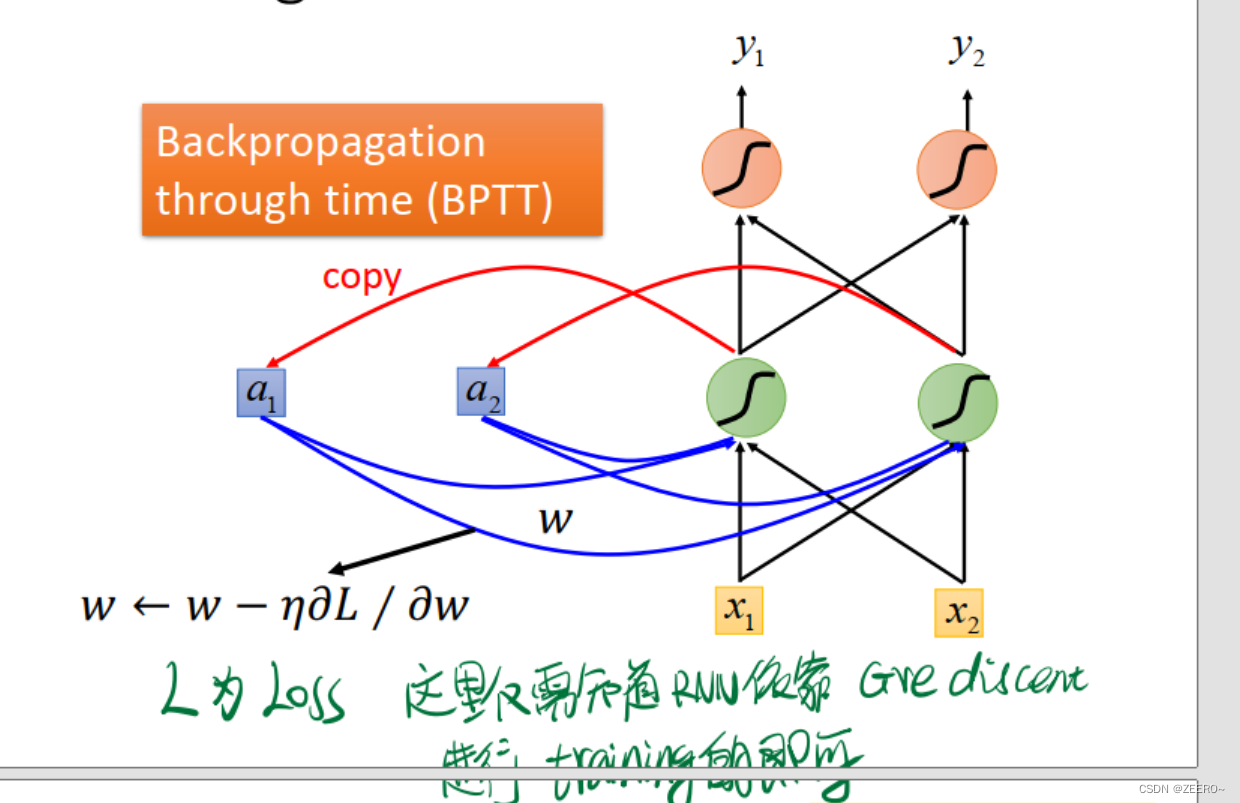
使用的方法呢，叫做BNPP(Backpropagation through time)，和一般的bp有细微的区别。



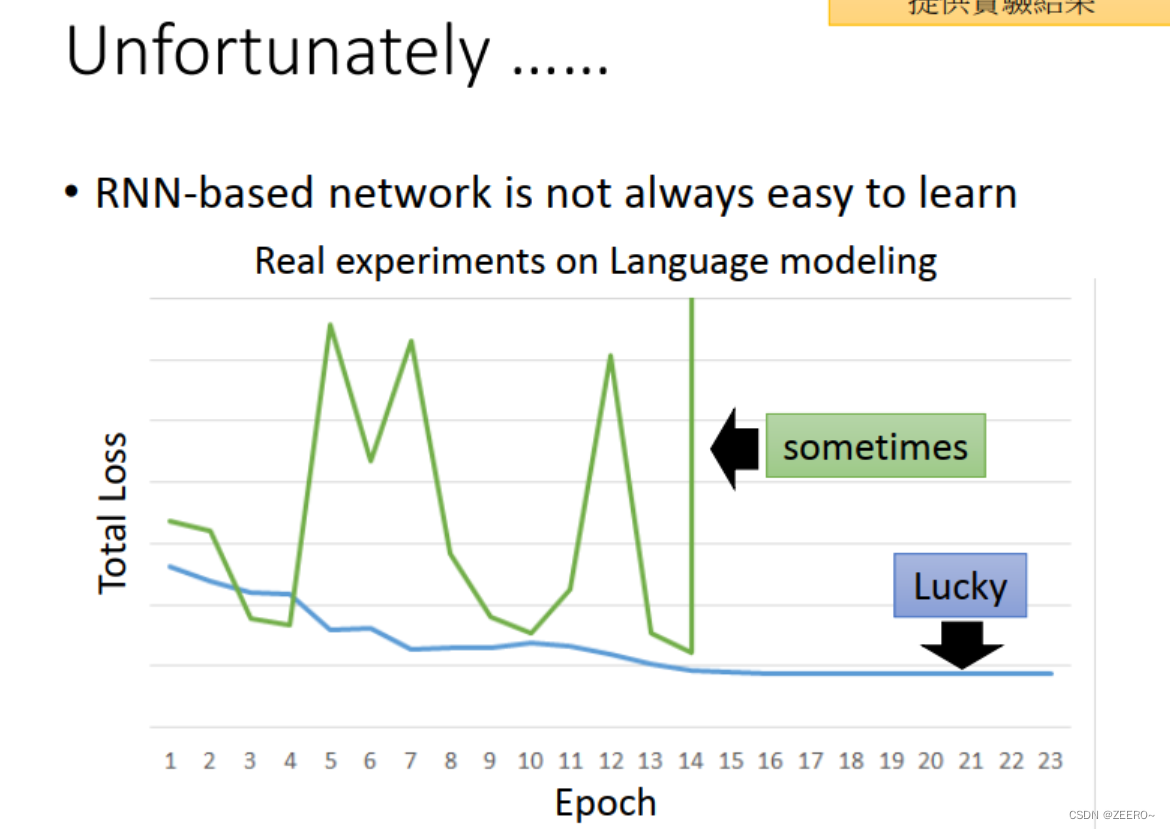
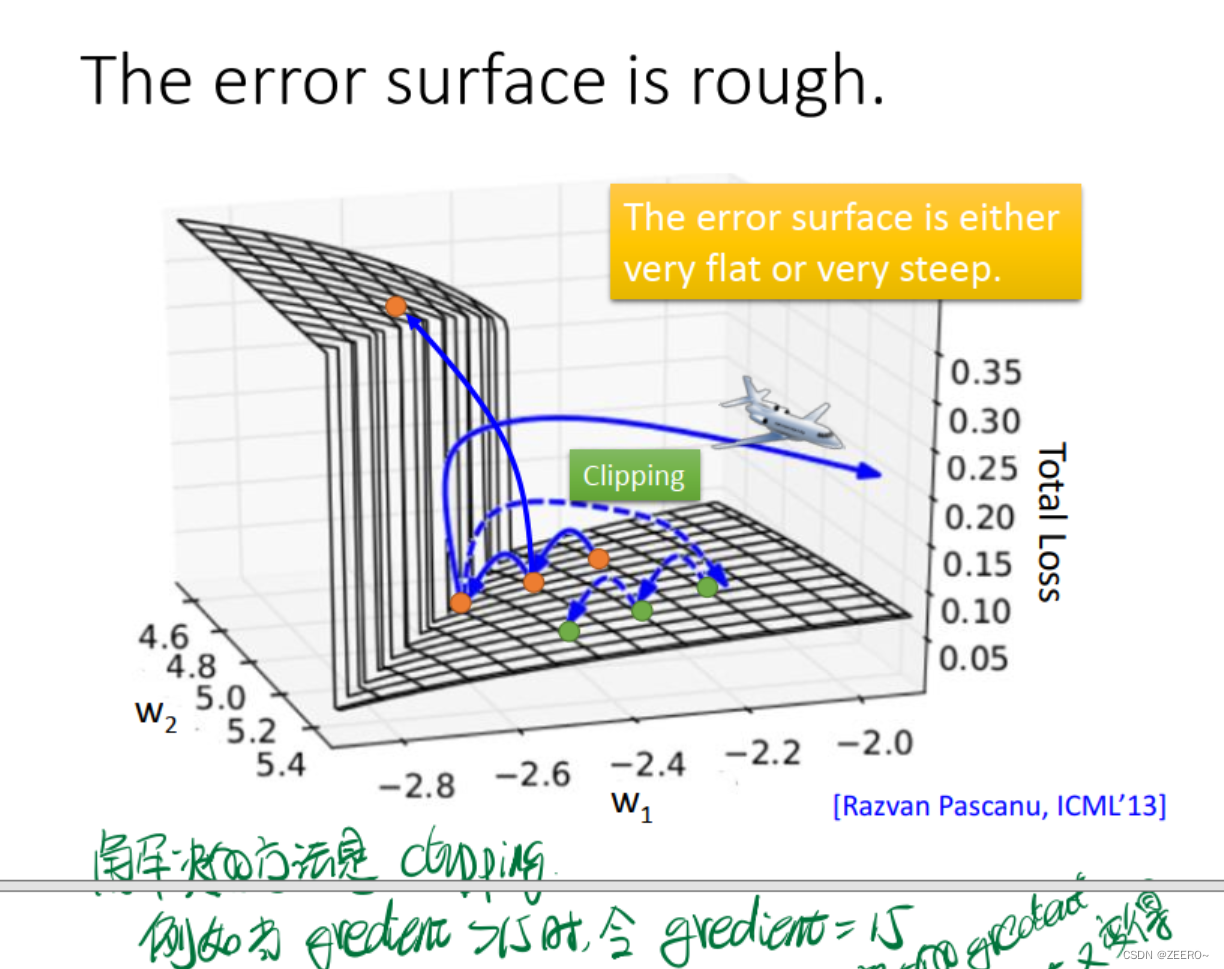
为何会出现这种情况呢，我们可以分析原因。

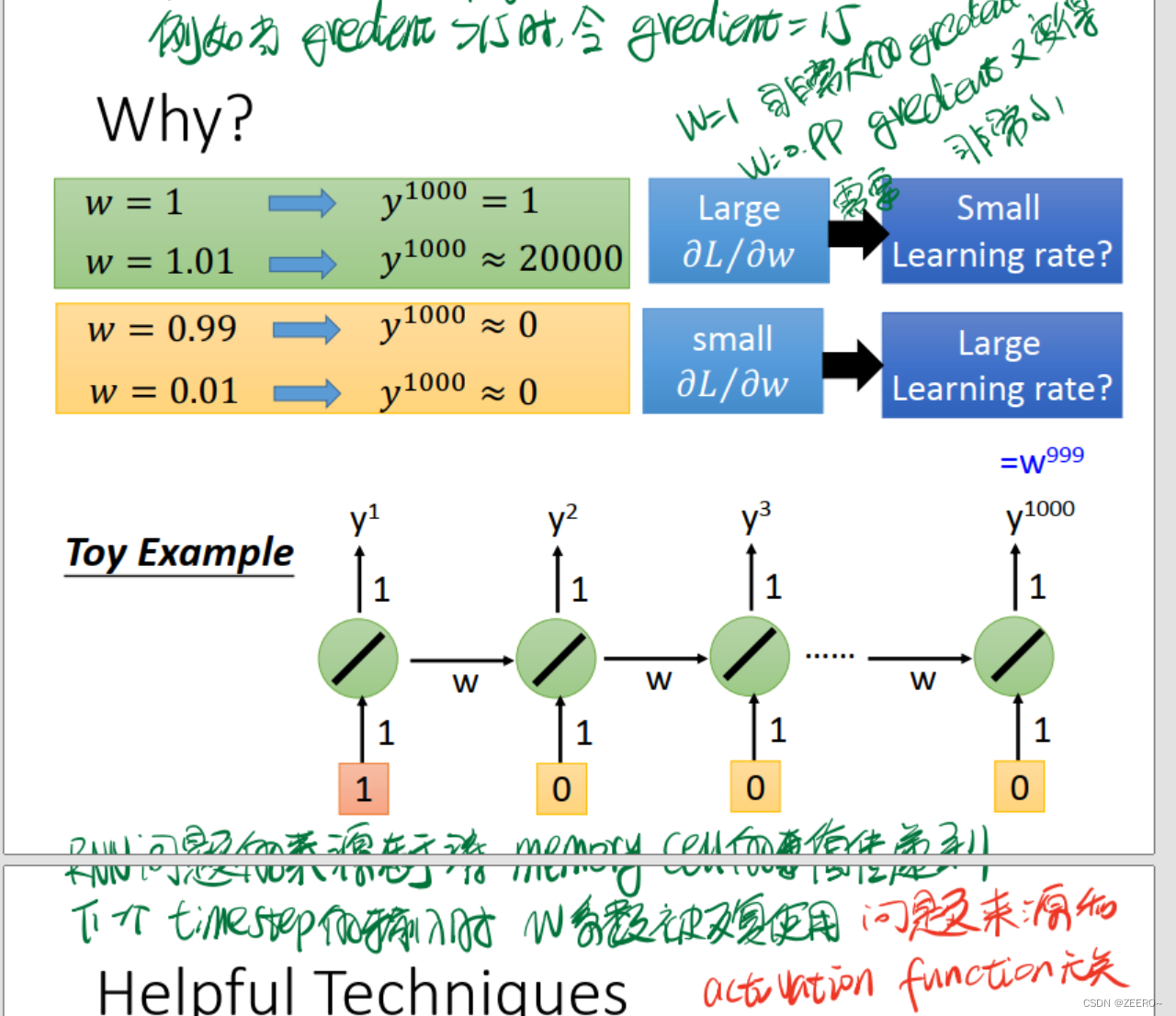
其实问题的来源，就是在于长序列导致的梯度消失或爆炸。一个非常实用的方法则是使用LSTM。
LSTM可以解决梯度消失的问题，但不能解决梯度爆炸的问题。

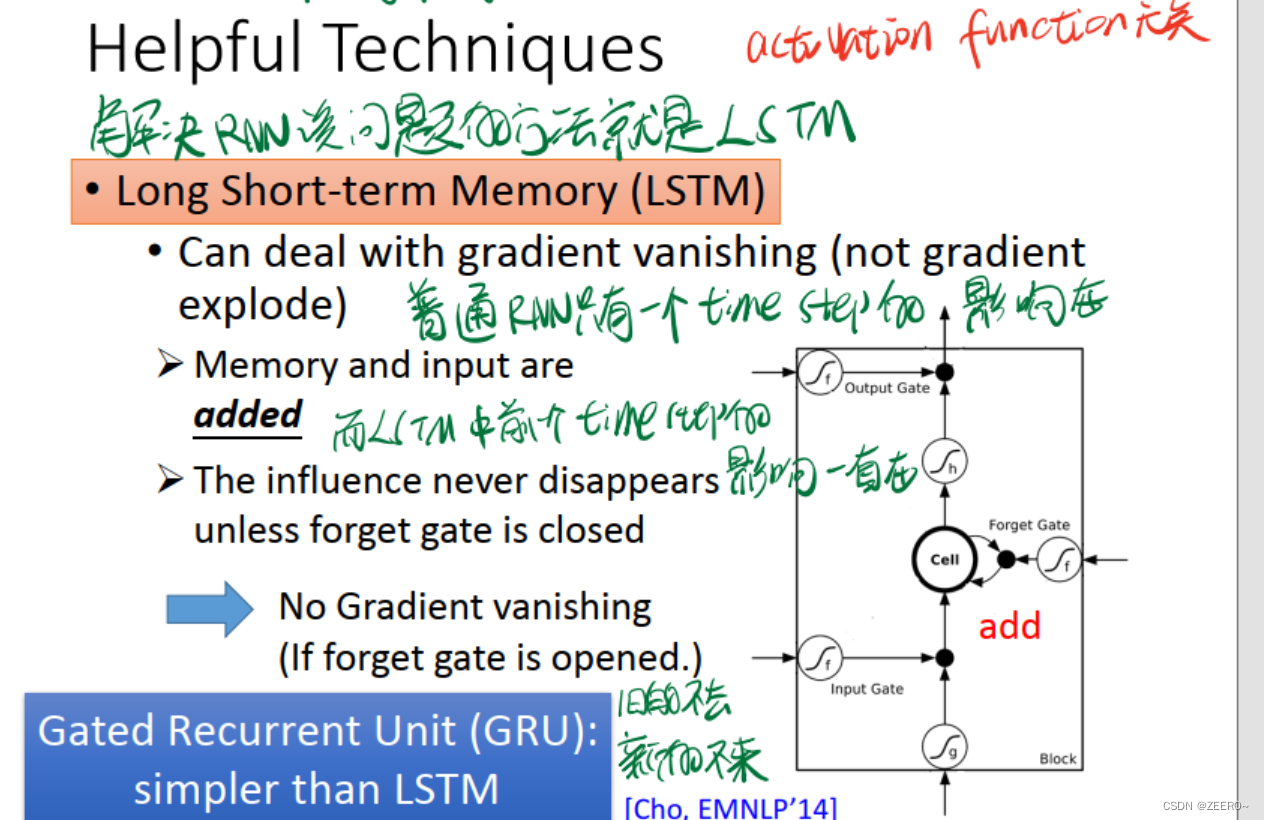
为什么LSTM可以解决梯度消失的问题呢。因为对于LSTM来说，前面每一个timestep中的信息，只要forget gate没有关闭，便会一直累加到最后。而普通的RNN，只会保留上一个timestep的信息。
一般来说，再设计LSTM网络结构时，需要做到使得大多数情况下forget gate是开启的，仅在少部分情况下forget gate会关闭。
另外一种LSTM的变种结构叫做GRU，GRU区别于LSTM，仅有2个gate。核心思想为旧的不去，新的不来。LSTM中的input gate和forget gate相互拮抗，只有forget gate关闭时，input gate才会打开。forget gate打开时，input gate则会关闭。

RNN与auto encoder和decoder

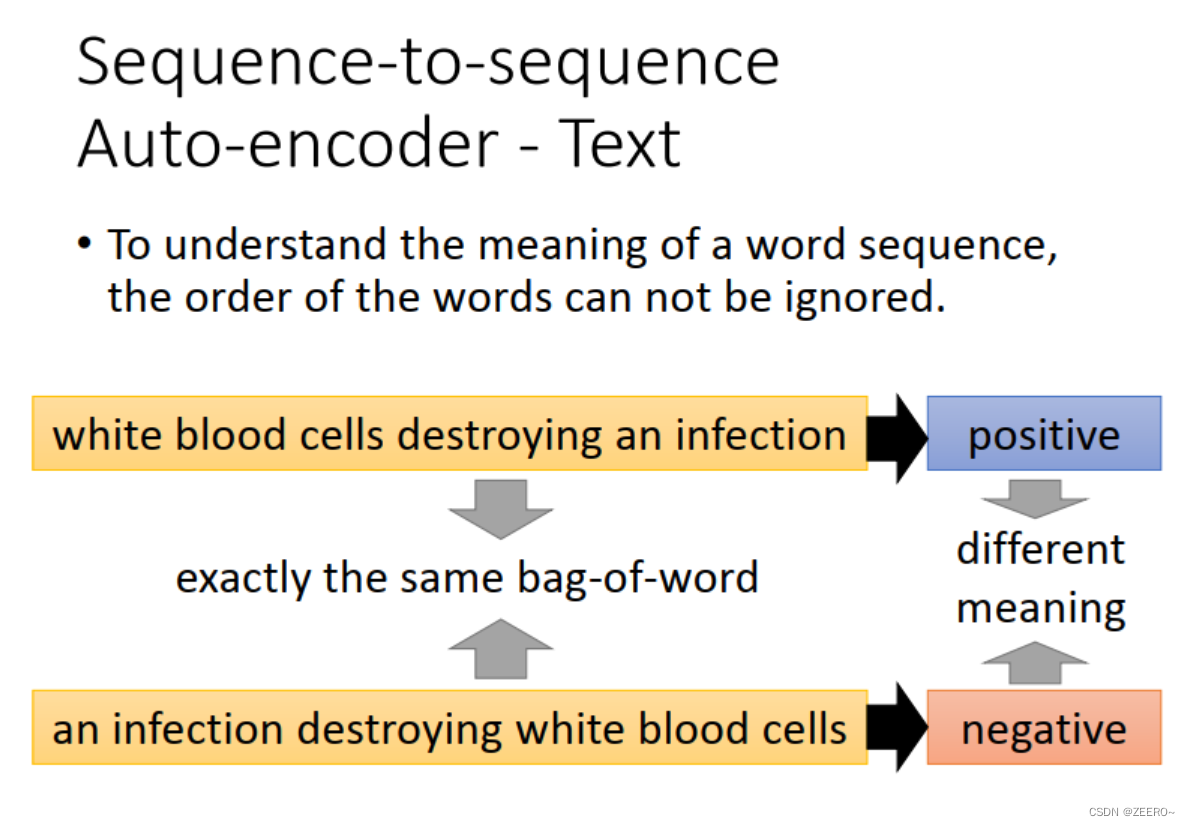
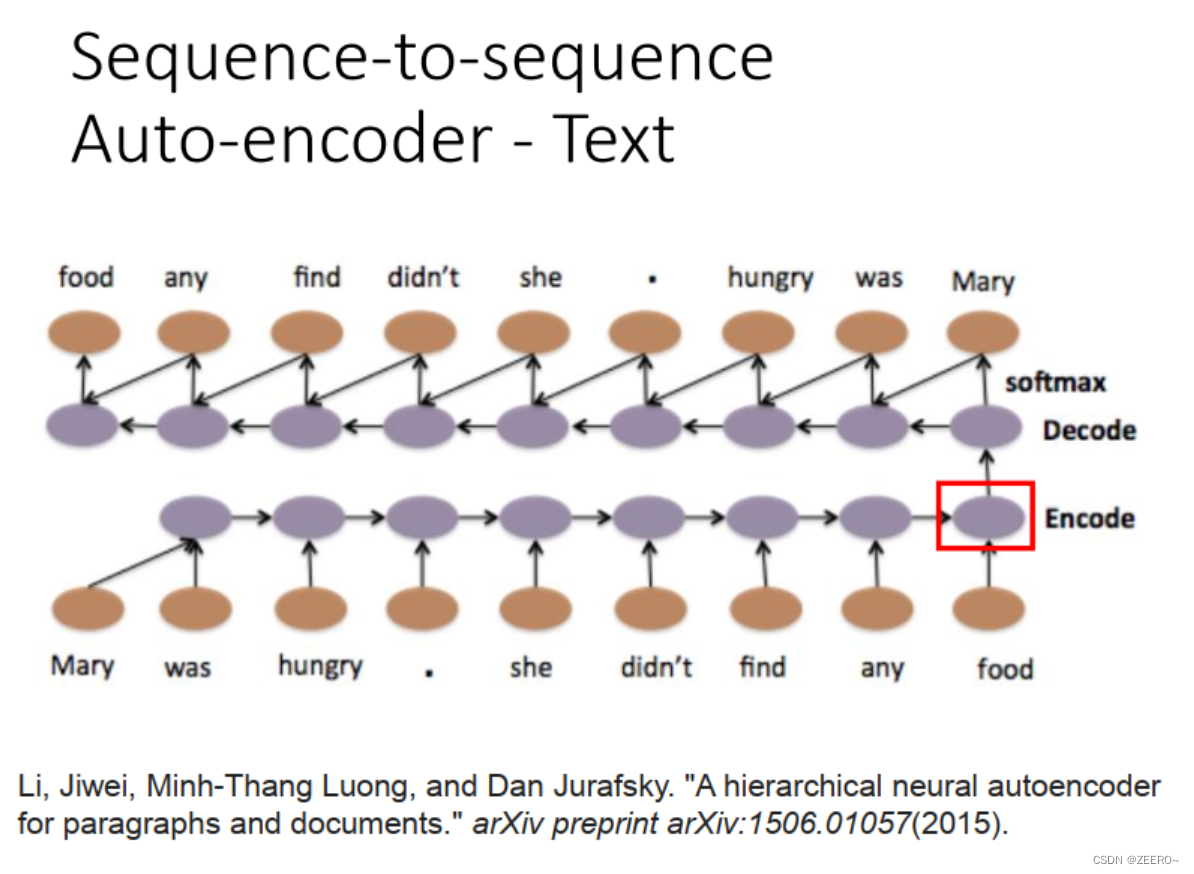
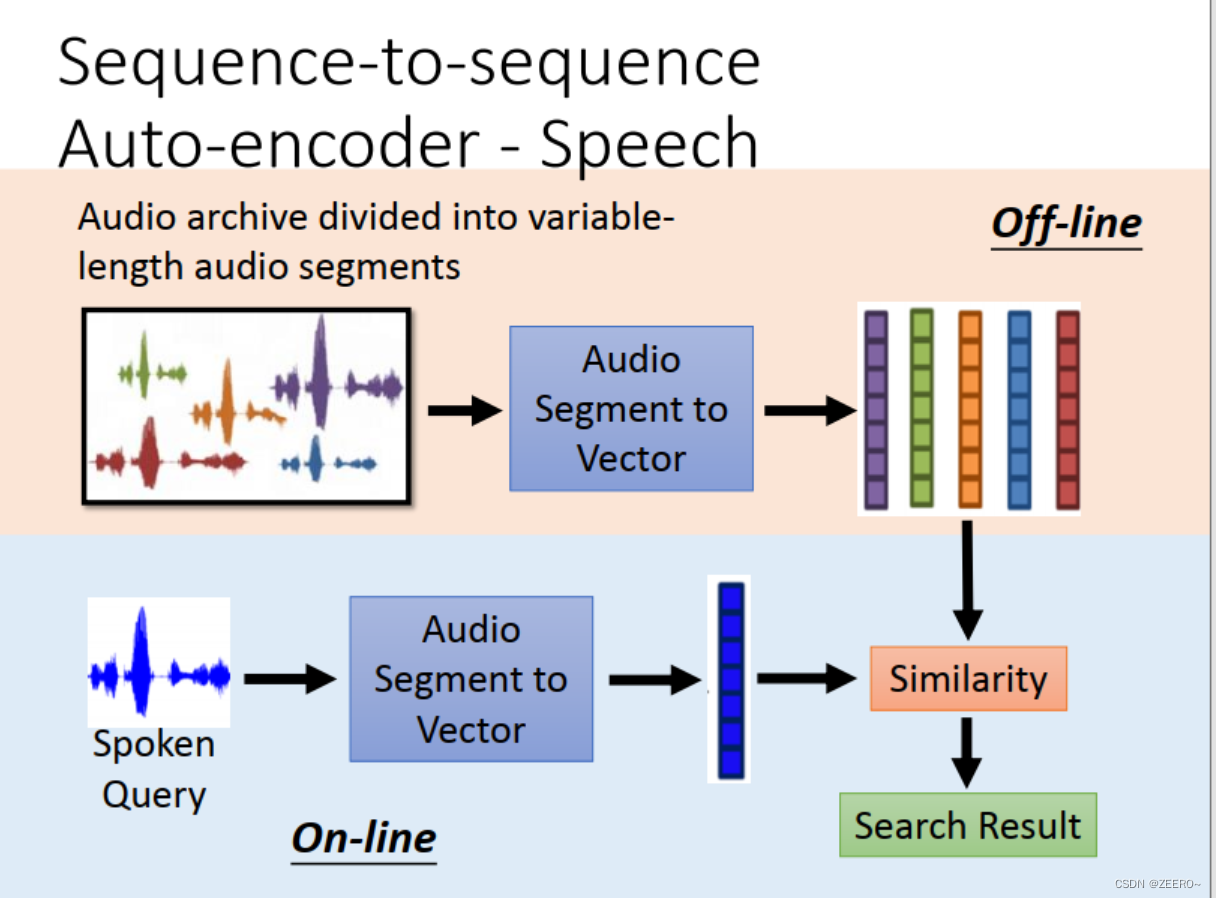
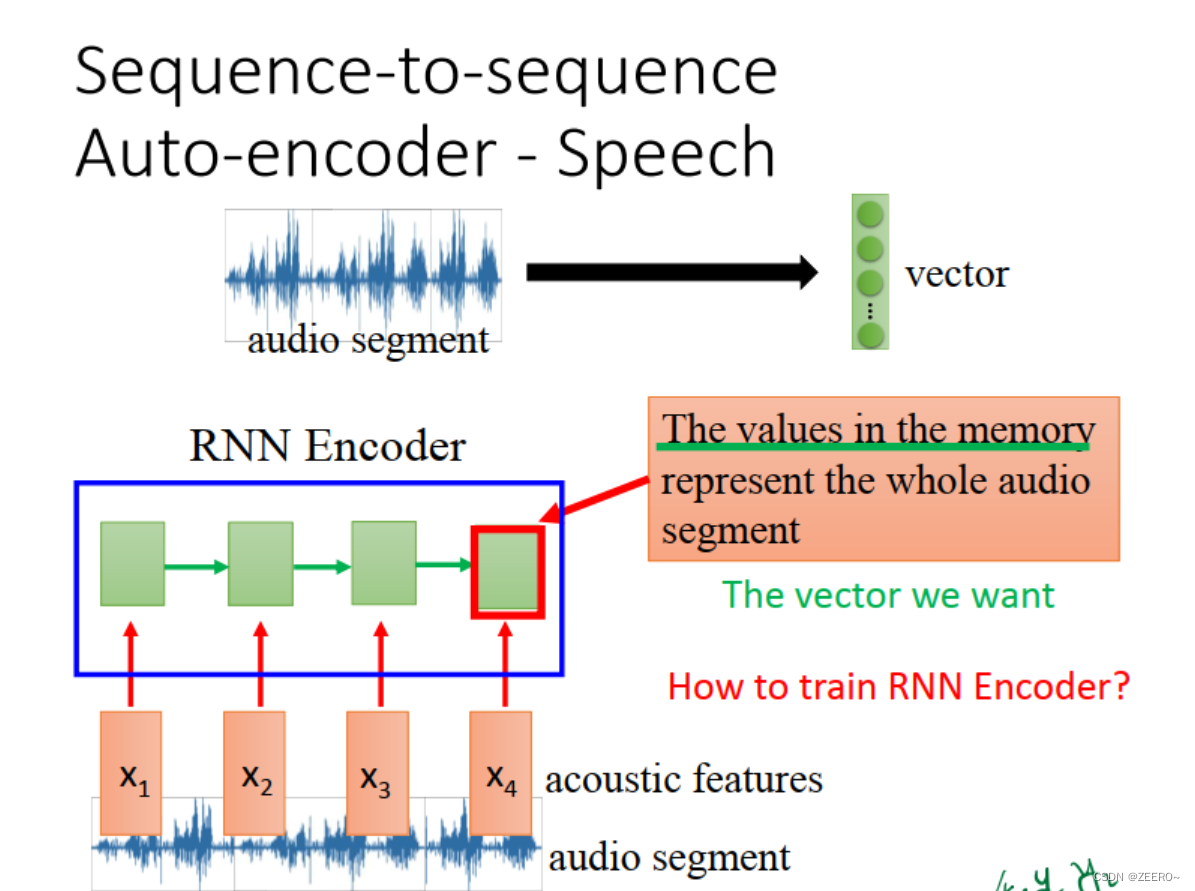
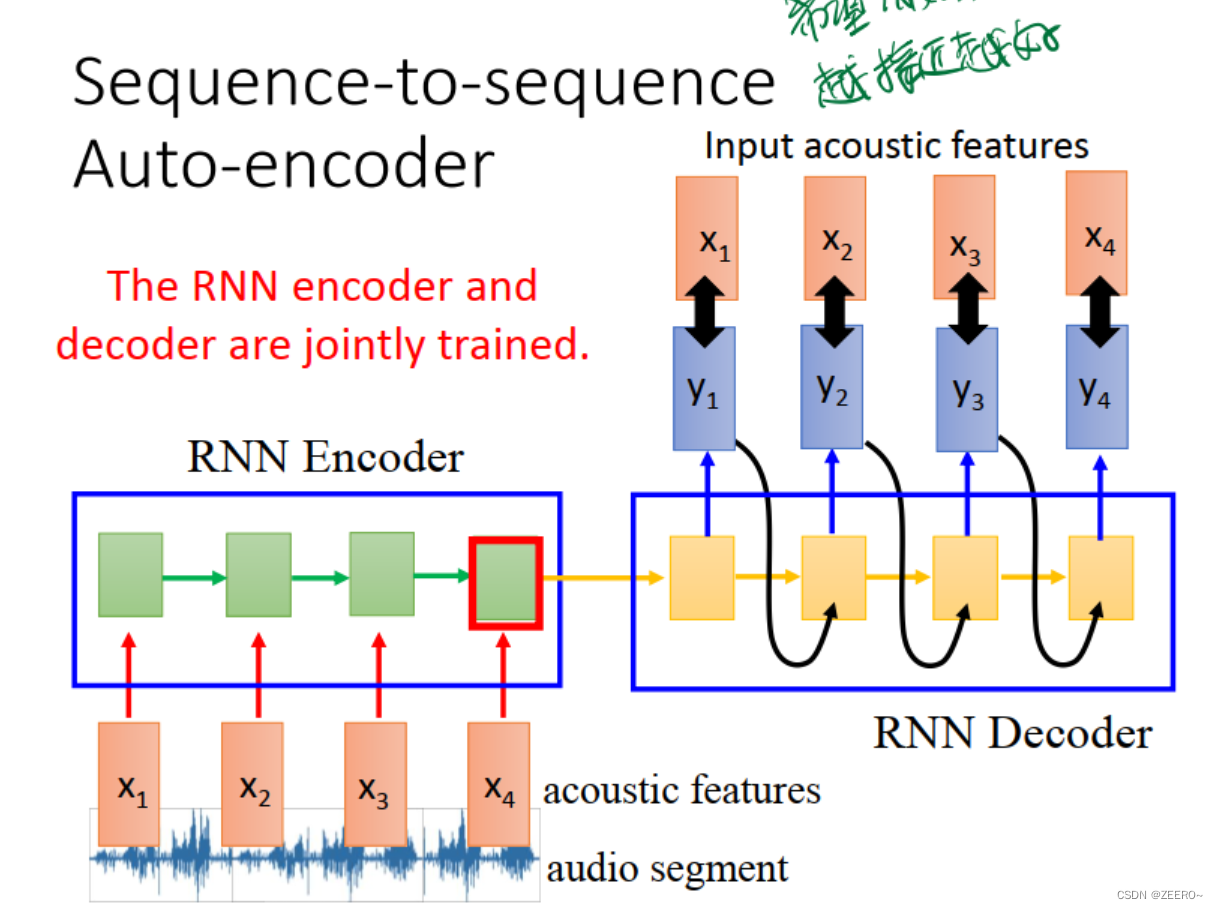
四、RNN和结构学习的区别

（1）从考虑上下文情况来看，单向RNN仅考虑到前文的信息，没有考虑到后文的信息。HMM如果使用viterbi算法的话，则同时考虑了整个sequence的信息。这里来看，结构学习似乎更有优势，但是，双向RNN也可以同时考虑整个sequence信息。
（2）RNN的cost和error是直接相关的，而结构学习并不是。cost往往高于error。
（3）最大的一个区别在于RNN可以deep，而结构学习在deep上则没有优势。

五、pytorch实现RNN与LSTM

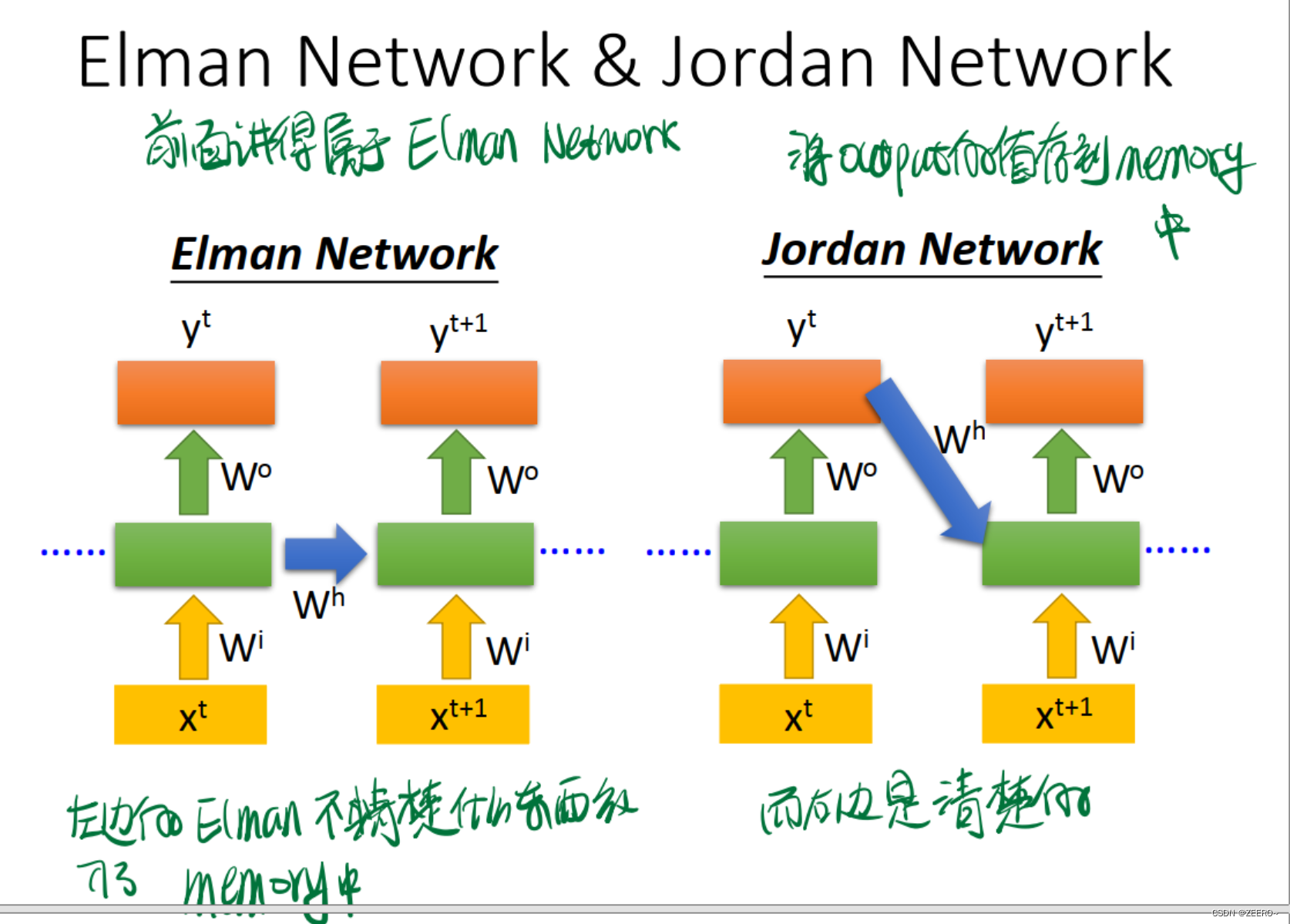
回忆一下我们最简单的Elman RNN网络结构。
看下官方文档如何实现：

$h_t$为当前时间t的hidden state。每一个time step，都会运行上面的公式。

可接受的输入参数如图。
（1）input_size，表示特征向量的维度，即输入的特征是多少维的。。
（2）hidden_size，表示hidden state的特征维度。
（3）num_layers，表示RNN的层数
（4）batch_first，这个参数决定入参是(seq,batch,feature)的形式还是(batch,seq,feature)的形式。RNN仅规定了这2种入参形式，为了迎合不同人的喜好，因此设定了这个参数作为模式切换。
注意，这里默认是batch_first=False的状态。
（5）bidirectional，决定了该RNN是否为双向RNN。

对于不使用batch的input来说，输入为$(L,H_{in})$。L为序列的长度，$H_{in}$为输入的特征维度
对于batch_first=True的来说，输入为$(N,L,H_{in})$，N为batch_size。
对于batch_first=False来说，输入为$(L,N,H_{in})$，N为batch_size。
$h_0$则表示初始的隐藏层状态。如果是双向RNN，则D=2，否则D=1。形状为$(D\ast nu{m}_{l}ayers,H_{out})$。如果使用了batch，则形状为$(D\ast nu{m}_{l}ayers,N,H_{out})$

输出为所有时间步的输出和最后一个时间步的隐层状态。
对于batch_first=True的情况来说，输出形状为$(N,L,D\ast H_{out})$。
$h_n$为最后一个time step的隐藏层状态，输出形状为$(D\ast numlayers,N,H_{out})$

官方给的例子如下：
建立一个RNN，输入的特征维度为10，hidden_state维度为20，num_layers=2。
输入为，seq_len=5,batch_size=3,$H_{in}=10。$
初始隐藏层状态为num_layers=2,batch_size=3,H_out=20。

当然，这里估计有人就想问，output的维度$H_{out}=20$，为什么会是20呢。别忘了，RNN的一个作用是可以进行分类。这里输出为20维的向量，通过torch.max()函数就可以获取预测的具体类别，也可以计算crossentropy。
另外提下，如果要将原始的数据转换成具有batch_size的形式，直接使用tensor自带的reshape函数即可。
至于nn.lstm模块，和nn.RNN模块大同小异，几乎可以直接copy过来。

5.1为何$H_{out}=hidde{n}_{s}ize$?

这里在看官方文档时，注意到了一个问题。

这里，一般来说,nn.RNN的输出并不是我们最后所得到的分类或回归的1个值。而是隐藏层变量的输出，作为下一个time step的输入。所以2者是相等的。
num_layers表示RNN堆叠的层数。

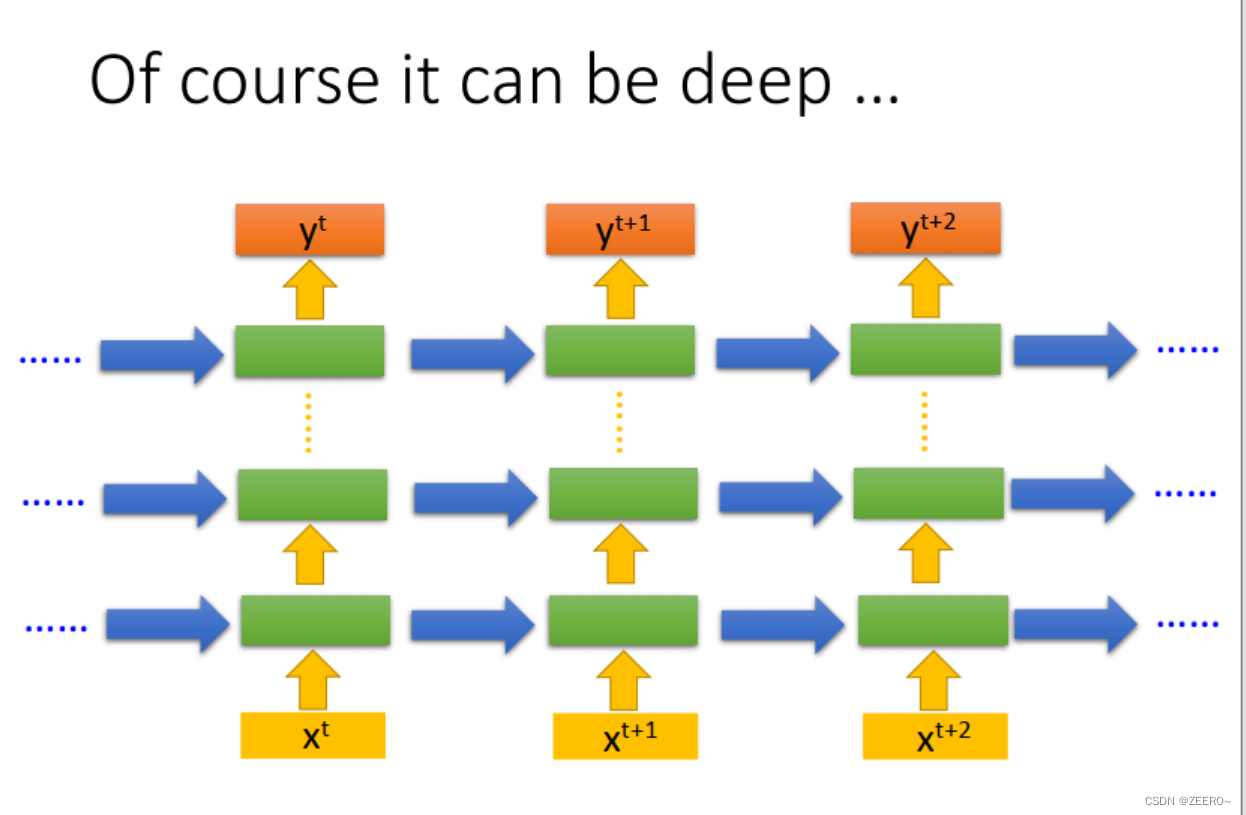
例如说如图所示情况下，假如忽略中间的竖直的省略号，则num_layers=3。普通情况下，双向RNN则num_layers也等于2.

5.2 LSTM的实现

前面讲LSTM的实现与RNN大同小异，其实还是有些区别的。来重点看下区别。


前面的定义就不细讲，通过前面的内容，肯定是可以理解上述的这些公式的。

定义的参数和RNN几乎没有任何区别，input_size还是表示输入特征的维度，hidden_size表示隐藏层的维度，num_layers表示网络层数等。最后多了一个proj_size，一般也用不太上。

网络参数的输入，有些区别，多了初始的隐藏层状态h0和c0，在RNN中只有h0。

output相比也知识多了一个c_n。

六、训练RNN时如何处理单步预测模型和多步预测问题

单步预测，指的是每个timestep都有一个对应的输出。
多步预测，指的是只在seq的最后一个再有输出值。

class LSTMModel(nn.Module):def __init__(self, input_dim, hidden_dim, output_dim):super(LSTMModel, self).__init__()self.hidden_dim = hidden_dimself.lstm = nn.LSTM(input_dim, hidden_dim, batch_first=True)  # 分别表示输入x的特征维度和中间隐藏层的特征维度self.linear = nn.Linear(hidden_dim, output_dim)def forward(self, input):  # batch_first=True。x严格按照batch_size,seq_len,feature的形式进行排列batch_size = input.size(0)seq_len = input.size(0)hidden_state = torch.zeros(1, batch_size, self.hidden_dim)cell_state = torch.zeros(1, batch_size, self.hidden_dim)output_seq, _ = self.lstm(input, (hidden_state, cell_state))  # 第2个为最后一个时间步的隐藏状态,output格式为[N,L,N*Hout]# last_hidden_state = output_seq[:, -1, :] #返回一个[N,1]的数据output = self.linear(output_seq)  # output size =[N,L,1]return output

区别就在于是否要注释中间那一行。在多步预测过程中，需要取1个batch_size中的每个seq_len的最后一个数值。