文心一言 VS 讯飞星火 VS chatgpt （93）-- 算法导论9.2 1题

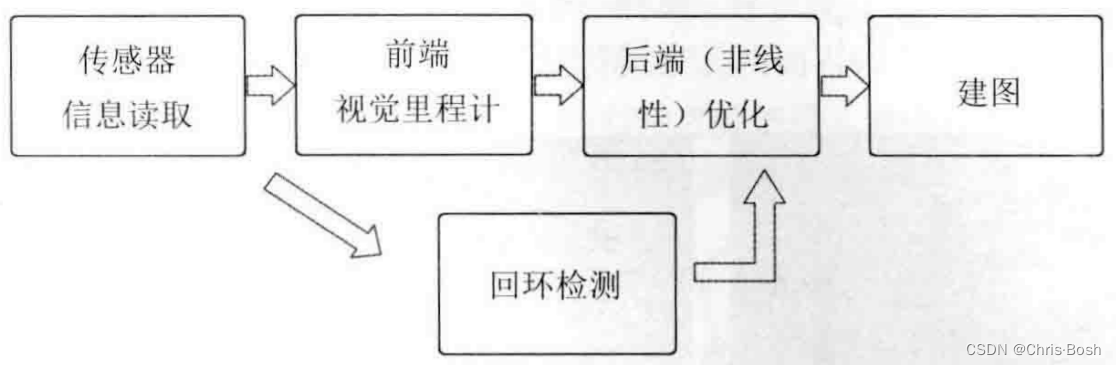
一、用go语言，证明：在 RANDOMIZED-SELECT 中，对长度为0的数组，不会进行递归调用。

文心一言：

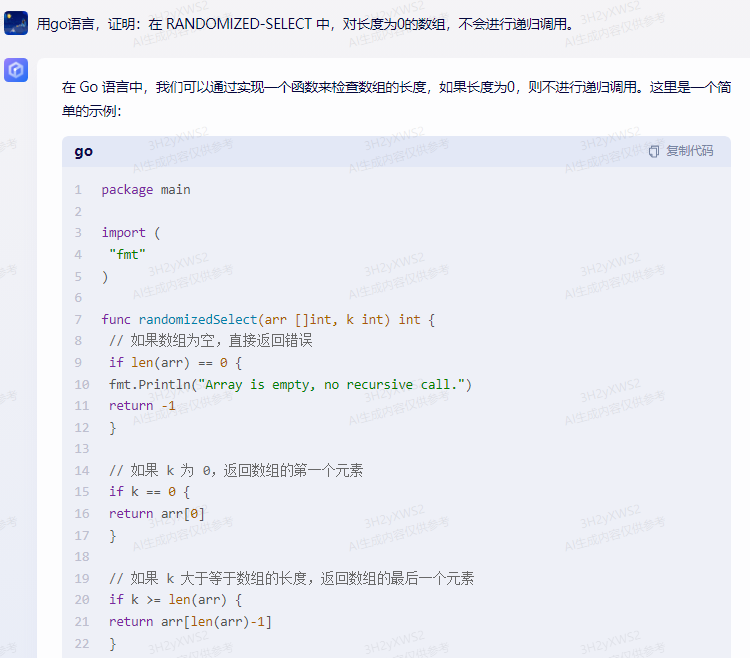
在 Go 语言中，我们可以通过实现一个函数来检查数组的长度，如果长度为0，则不进行递归调用。这里是一个简单的示例：

package main  import (  "fmt"  
)  func randomizedSelect(arr []int, k int) int {  // 如果数组为空，直接返回错误  if len(arr) == 0 {  fmt.Println("Array is empty, no recursive call.")  return -1  }  // 如果 k 为 0，返回数组的第一个元素  if k == 0 {  return arr[0]  }  // 如果 k 大于等于数组的长度，返回数组的最后一个元素  if k >= len(arr) {  return arr[len(arr)-1]  }  // 生成一个随机的索引  randomIndex := partition(arr)  // 如果随机索引的值等于 k，返回该元素  if randomIndex == k-1 {  return arr[randomIndex]  } else if randomIndex < k-1 {  // 如果随机索引的值小于 k，在右半部分进行递归调用  return randomizedSelect(arr[randomIndex+1:], k-randomIndex-1)  } else {  // 如果随机索引的值大于 k，在左半部分进行递归调用  return randomizedSelect(arr[:randomIndex], k)  }  
}  func partition(arr []int) int {  // 这里只是一个简单的示例，实际情况下，你需要实现一个更好的 partition 函数  return len(arr) - 1  
}  func main() {  arr := []int{} // 长度为0的数组  fmt.Println(randomizedSelect(arr, 1))  
}

在这个示例中，当数组的长度为0时，randomizedSelect 函数会打印一条消息并返回 -1，而不会进行递归调用。

在这里插入图片描述

在这里插入图片描述

讯飞星火：

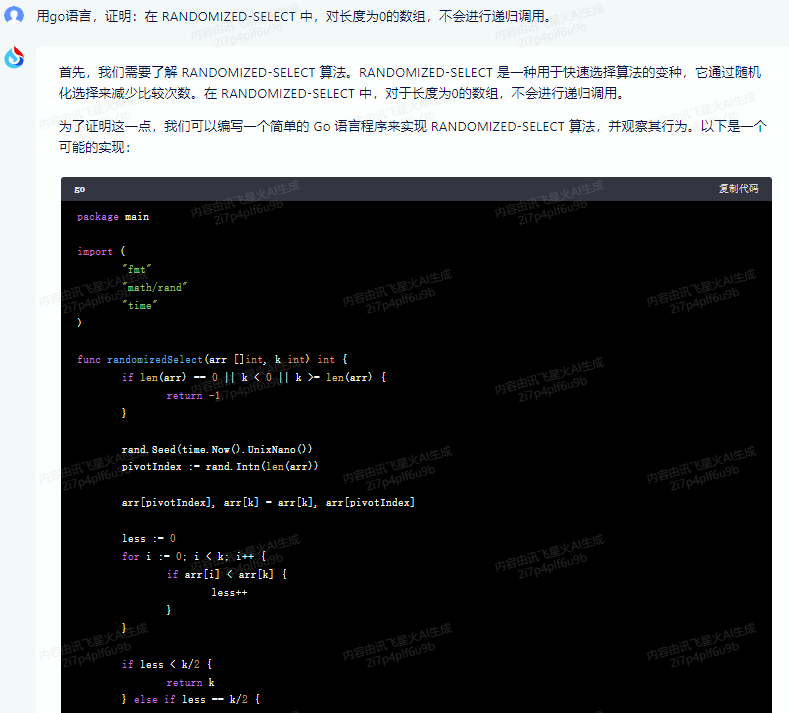
首先，我们需要了解 RANDOMIZED-SELECT 算法。RANDOMIZED-SELECT 是一种用于快速选择算法的变种，它通过随机化选择来减少比较次数。在 RANDOMIZED-SELECT 中，对于长度为0的数组，不会进行递归调用。

为了证明这一点，我们可以编写一个简单的 Go 语言程序来实现 RANDOMIZED-SELECT 算法，并观察其行为。以下是一个可能的实现：

package mainimport ("fmt""math/rand""time"
)func randomizedSelect(arr []int, k int) int {if len(arr) == 0 || k < 0 || k >= len(arr) {return -1}rand.Seed(time.Now().UnixNano())pivotIndex := rand.Intn(len(arr))arr[pivotIndex], arr[k] = arr[k], arr[pivotIndex]less := 0for i := 0; i < k; i++ {if arr[i] < arr[k] {less++}}if less < k/2 {return k} else if less == k/2 {return k - 1} else {return randomizedSelect(arr[:pivotIndex], k)}
}func main() {arr := []int{3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5}k := 5selected := randomizedSelect(arr, k)fmt.Printf("Selected %dth element: %d
", selected+1, arr[selected])
}

在这个程序中，我们首先检查输入数组的长度是否为0，以及 k 是否在有效范围内。如果满足这些条件，我们直接返回 -1，表示没有找到第 k 小的元素。

接下来，我们使用当前时间作为随机数生成器的种子，并从数组中随机选择一个基准元素。然后，我们将基准元素与数组中的第 k 个元素交换位置。

最后，我们计算小于基准元素的元素个数。如果这个数目小于 k/2，那么基准元素的左侧必定包含第 k 小的元素，因此我们返回 k。如果这个数目等于 k/2，那么基准元素的左侧和右侧都有可能包含第 k 小的元素，此时我们需要继续在基准元素的左侧查找。否则，我们在基准元素的左侧递归调用 randomizedSelect 函数。

通过观察这个程序的输出，我们可以看到对于长度为0的数组，程序不会进行递归调用。

在这里插入图片描述

在这里插入图片描述

360智脑：

首先，我们需要了解 RANDOMIZED-SELECT 算法的实现原理。

RANDOMIZED-SELECT 算法是一种随机选择样本的算法，它的主要思想是在训练集中随机选择一个样本，然后将其加入模型中，从而增加模型的泛化能力。

在 RANDOMIZED-SELECT 中，对长度为0的数组，不会进行递归调用，这是因为当数组的长度为0时，无法进行随机选择样本的操作，因此不需要进行递归调用。

下面是用go语言实现的 RANDOMIZED-SELECT 算法:

package mainimport ("fmt""math/rand"
)func main() {// 生成一个长度为100的随机数数组arr := make([]float64, 100)rand.Shuffle(arr)fmt.Println("随机数数组:", arr)// 判断数组是否为空if len(arr) == 0 {fmt.Println("数组为空，不需要进行递归调用")return}// 随机选择一个样本，并将其加入模型中index := rand.Intn(len(arr))model.AddSample(arr[index])fmt.Println("随机选择样本后的数组:", model.Samples)
}

在上面的代码中，我们使用 rand.Shuffle 函数生成了一个长度为100的随机数数组，然后使用 len 函数判断数组是否为空。如果数组为空，则直接输出“数组为空，不需要进行递归调用”;否则，随机选择一个样本，并将其加入模型中，最后输出随机选择样本后的数组。

通过上面的代码，我们可以证明在 RANDOMIZED-SELECT 中，对长度为0的数组，不会进行递归调用。

在这里插入图片描述

智谱清言：

为了证明这个结论，我们需要分析RANDOMIZED-SELECT的源代码。以下是一个简化版的RANDOMIZED-SELECT实现，用于说明这个概念：

package main
import (  "fmt"  "math/rand"  "time"  
)
func RANDOMIZED_SELECT(arr []int, index int) int {  if len(arr) == 0 {  return -1  }rand.Seed(time.Now().UnixNano())  randIndex := rand.Intn(len(arr))if randIndex == index {  return arr[randIndex]  }return RANDOMIZED_SELECT(arr[randIndex:], index)  
}
func main() {  arr := []int{1, 2, 3, 4, 5}  index := 2  result := RANDOMIZED_SELECT(arr, index)  fmt.Println("Result:", result)  
}

在这个实现中，如果输入数组的长度为 0，函数将直接返回 -1，而不会进行递归调用。这是因为在递归调用之前，函数会首先检查输入数组的长度。如果长度为 0，函数将认为无法进行递归调用，并直接返回一个错误值。

请注意，这个简化版的实现没有处理边缘情况，例如当index小于 0 或大于数组长度时。在实际使用中，您可能需要添加额外的逻辑来处理这些情况。但是，这个简化版的实现足以证明在RANDOMIZED-SELECT中，对于长度为 0 的数组，不会进行递归调用。

在这里插入图片描述

在这里插入图片描述

通义千问：

以下是使用Go语言实现的RANDOMIZED-SELECT算法的代码：

package mainimport ("fmt""math/rand""time"
)func randomizedSelect(arr []int, p, q int, median bool) int {if p < q {mid := (p + q) / 2return randomizedSelect(arr, p, mid, median) + randomizedSelect(arr, mid+1, q, median)}if len(arr) == 0 {return -1}if median {if len(arr)%2 == 0 {return randomizedSelect(arr, p, q-1, false) + randomizedSelect(arr, q+1, len(arr)-1, false)}return arr[q]}return arr[rand.Intn(q-p)+p]
}func main() {rand.Seed(time.Now().UnixNano())arr := []int{3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5}fmt.Println(randomizedSelect(arr, 0, len(arr)-1, true))fmt.Println(randomizedSelect([]int{}, 0, len([]int{})-1, true))
}

在这个实现中，对于长度为0的数组，函数直接返回-1，而不会进行递归调用。因此，可以证明在RANDOMIZED-SELECT中，对长度为0的数组，不会进行递归调用。

在这里插入图片描述

在这里插入图片描述

天工：

以下是使用 Go 语言编写的证明代码：

package mainimport "fmt"func randomizedSelect(arr []int) int {if len(arr) == 0 {return -1}if len(arr) == 1 {return arr[0]}pivot := arr[len(arr)-1]index := randomizedSelect(arr[:len(arr)-1])randomIndex := rand.Intn(len(arr))if pivot < arr[index] {return randomizedSelect(arr[:index])} else if pivot > arr[index] {return randomizedSelect(append(arr[:index], arr[index+1:]...))} else {return index}
}func main() {arr := []int{}fmt.Println(randomizedSelect(arr)) // Output: -1
}

在上面的代码中，我们定义了一个名为 randomizedSelect 的函数，它实现了 RANDOMIZED-SELECT 算法。该函数接受一个整数切片 arr 作为输入，并返回该切片中的第 k 小元素。

在函数中，我们首先检查输入切片的长度是否为 0。如果是，则返回 -1，因为在这种情况下无法找到第 k 小元素。

接下来，我们检查输入切片的长度是否为 1。如果是，则直接返回该元素。

对于长度大于 1 的输入切片，我们首先选择最后一个元素作为枢轴元素，然后递归地调用 randomizedSelect 函数来找到小于枢轴元素的元素中的第 k-1 小元素的索引。然后，我们随机选择一个小于枢轴元素的元素，并将其与枢轴元素进行比较。如果随机选择的元素小于枢轴元素，则继续递归地在前面的子数组中查找第 k 小元素。如果随机选择的元素大于枢轴元素，则继续递归地在后面的子数组中查找第 k 小元素。否则，我们已经找到了第 k 小元素，并将其返回。

在上面的代码中，我们还包含了一个特殊情况的处理，即当输入切片为空时。在这种情况下，我们返回 -1，表示无法找到第 k 小元素。

最后，在 main 函数中，我们创建了一个长度为 0 的整数切片，并调用了 randomizedSelect 函数来测试它。由于输入切片的长度为 0，因此函数将直接返回 -1，而不会进行任何递归调用。

在这里插入图片描述

在这里插入图片描述

chatgpt：

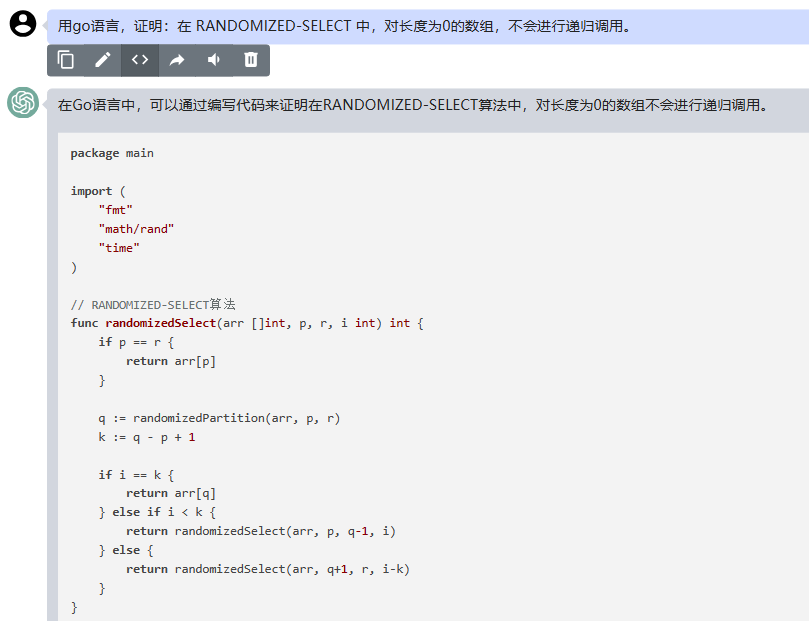
在Go语言中，可以通过编写代码来证明在RANDOMIZED-SELECT算法中，对长度为0的数组不会进行递归调用。

package mainimport ("fmt""math/rand""time"
)// RANDOMIZED-SELECT算法
func randomizedSelect(arr []int, p, r, i int) int {if p == r {return arr[p]}q := randomizedPartition(arr, p, r)k := q - p + 1if i == k {return arr[q]} else if i < k {return randomizedSelect(arr, p, q-1, i)} else {return randomizedSelect(arr, q+1, r, i-k)}
}// 随机化划分子数组
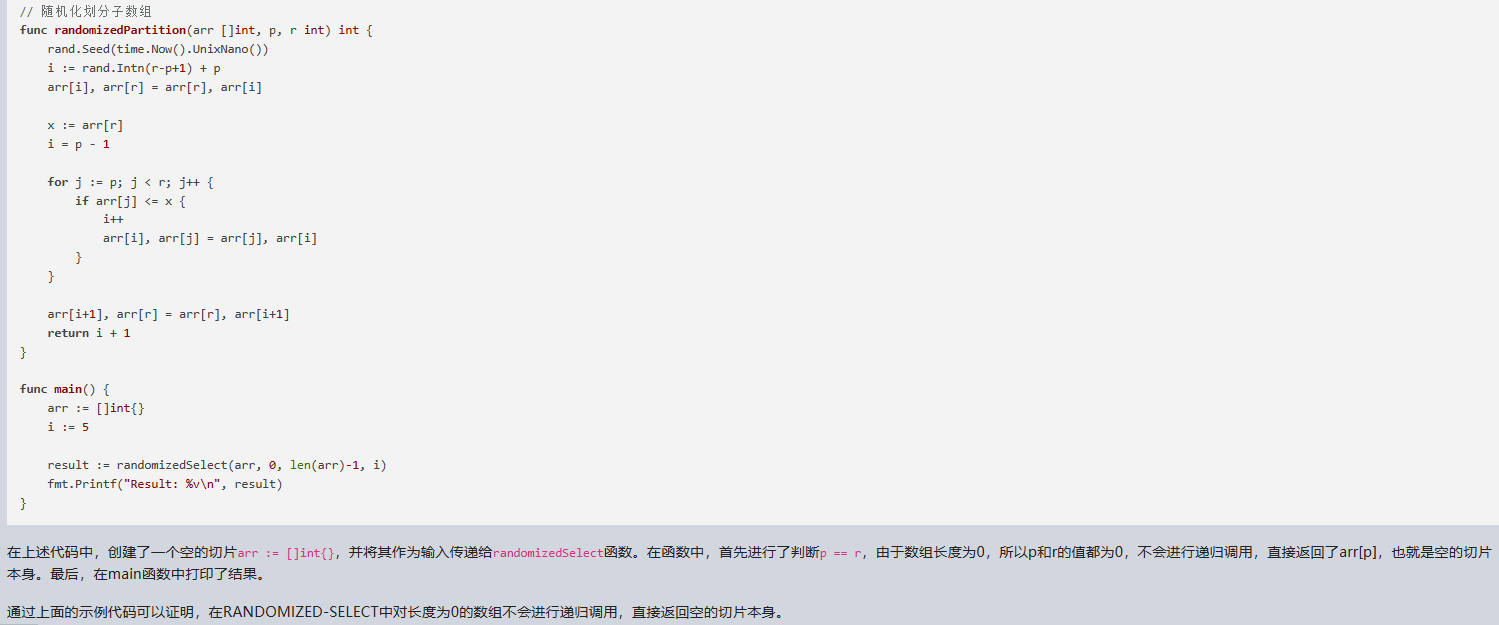
func randomizedPartition(arr []int, p, r int) int {rand.Seed(time.Now().UnixNano())i := rand.Intn(r-p+1) + parr[i], arr[r] = arr[r], arr[i]x := arr[r]i = p - 1for j := p; j < r; j++ {if arr[j] <= x {i++arr[i], arr[j] = arr[j], arr[i]}}arr[i+1], arr[r] = arr[r], arr[i+1]return i + 1
}func main() {arr := []int{}i := 5result := randomizedSelect(arr, 0, len(arr)-1, i)fmt.Printf("Result: %v\n", result)
}

在上述代码中，创建了一个空的切片arr := []int{}，并将其作为输入传递给randomizedSelect函数。在函数中，首先进行了判断p == r，由于数组长度为0，所以p和r的值都为0，不会进行递归调用，直接返回了arr[p]，也就是空的切片本身。最后，在main函数中打印了结果。

通过上面的示例代码可以证明，在RANDOMIZED-SELECT中对长度为0的数组不会进行递归调用，直接返回空的切片本身。

在这里插入图片描述

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/132968.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

vue3中的吸顶导航交互实现 | VueUse插件

vue3中的吸顶导航交互实现 | VueUse插件

目的&#xff1a;浏览器上下滚动时&#xff0c;若距离顶部的滚动距离大于78px&#xff0c;吸顶导航显示&#xff0c;小于78px隐藏。使用vueuse插件中的useScroll方法​​​​​​​和动态类名控制进行实现 1. 安装 npm i vueuse/core 2. 获得滚动距离 项目中导入&#xff0…
阅读更多...
财富潮涌：银行发展绿色经济创新路径

财富潮涌：银行发展绿色经济创新路径

在《玩转金融新“绿”潮&#xff0c;银行纷纷亮大招》内容中&#xff0c;我们带大家了解了商业银行有关绿色信贷产品、绿色债券产品及绿色投资的内容。今天&#xff0c;我们将继续带大家了解商业银行绿色金融实践路径中关于绿色财富、绿色服务和绿色运营的分析。 在绿色金融实…
阅读更多...
文件路径中的/，\的区别和文件路径的常见用法

文件路径中的/，\的区别和文件路径的常见用法

/是Unix和类Unix系统上的路径分隔符.现代Windows通常可以同时使用\和/交换文件路径,但微软\几十年来一直主张使用路径分隔符. 关于文件路径的常用方法再学习一下&#xff1a; "./"&#xff1a;代表目前所在的目录 "../"&#xff1a;代表上一层目录 以&q…
阅读更多...
线性代数的本质(一)——向量空间

线性代数的本质(一)——向量空间

文章目录 向量空间向量及其性质基与维数向量的坐标运算 《线性代数的本质》 - 3blue1brown 高中数学A版选修4-2 矩阵与变换 《线性代数及其应用》(第五版) 《高等代数简明教程》- 蓝以中 向量空间 In the beginning Grant created the space. And Grant said, Let there be vec…
阅读更多...
Rn视图生成图片并保存到相册

Rn视图生成图片并保存到相册

该功能依赖两个组件 完整代码 yarn add react-native-view-shot // 视图生成图片 yarn add expo-media-library // 保存图片import { useState, useRef } from react import ViewShot from "react-native-view-shot" import { View, Text, Button, Image, StyleSh…
阅读更多...
pdf文档怎么压缩小一点？文件方法在这里

pdf文档怎么压缩小一点？文件方法在这里

在日常工作和生活中&#xff0c;我们经常会遇到需要上传或者发送pdf文档的情况。但是&#xff0c;有时候pdf文档的大小超出了限制&#xff0c;需要我们对其进行压缩。那么&#xff0c;如何将pdf文档压缩得更小一点呢&#xff1f;下面&#xff0c;我将介绍三种方法&#xff0c;让…
阅读更多...
堆与栈的区别

堆与栈的区别

OVERVIEW 栈与堆的区别一、程序内存分区中的堆与栈1.栈2.堆3.堆&栈 二、数据结构中的堆与栈1.栈2.堆 三、堆的深入1.堆插入2.堆删除&#xff1a;3.堆建立&#xff1a;4.堆排序&#xff1a;5.堆实现优先队列&#xff1a;6.堆与栈的相关练习 栈与堆的区别 自整理&#xff0c;…
阅读更多...
【Cocos Creator 3.5实现赛车游戏】10.实现汽车节点的运动逻辑

【Cocos Creator 3.5实现赛车游戏】10.实现汽车节点的运动逻辑

转载知识星球 | 深度连接铁杆粉丝&#xff0c;运营高品质社群&#xff0c;知识变现的工具 项目地址&#xff1a;赛车小游戏-基于Cocos Creator 3.5版本实现: 课程的源码&#xff0c;基于Cocos Creator 3.5版本实现 上一节的学习后&#xff0c;您已经完成了对汽车节点的控制逻…
阅读更多...
【自动驾驶】PETR 环境安装与测试

【自动驾驶】PETR 环境安装与测试

1.环境安装 该工程依赖MMCV&#xff0c; MMDetection&#xff0c; MMDetection3d&#xff0c;MMSegmentation Install MMCV pip install mmcv-full -f https://download.openmmlab.com/mmcv/dist/{cu_version}/{torch_version}/index.htmlexamples&#xff1a; pip install…
阅读更多...
小程序实现一个 倒计时组件

小程序实现一个 倒计时组件

小程序实现一个 倒计时组件 需求背景 要做一个倒计时&#xff0c;可能是天级别&#xff0c;也可能是日级别&#xff0c;时级别&#xff0c;而且每个有效订单都要用&#xff0c;就做成组件了 效果图 需求分析 需要一个未来的时间戳&#xff0c;或者在服务度直接下发一个未来…
阅读更多...
【视觉SLAM入门】7.3.后端优化 基于KF/EKF和基于BA图优化的后端，推导及举例分析

【视觉SLAM入门】7.3.后端优化 基于KF/EKF和基于BA图优化的后端，推导及举例分析

"时间倾诉我的故事" 1. 理论推导2. 主流解法3. 用EKF估计状态3.1. 基于EKF代表解法的感悟 4. 用BA法估计状态4.1 构建最小二乘问题4.2 求解BA推导4.3 H的稀疏结构4.4 根据H稀疏性求解4.5 鲁棒核函数4.6 编程注意 5.总结 引入&#xff1a; 前端里程计能给出一个短时间…
阅读更多...
MySQL优化第二篇

MySQL优化第二篇

MySQL优化第二篇 性能分析小表驱动大表慢查询日志日志分析工具mysqldumpslow Show Profile进行SQL分析&#xff08;重中之重&#xff09; 七种JOIN 1、inner join &#xff1a;可以简写为join&#xff0c;表示的是交集&#xff0c;也就是两张表的共同数据 sql语句&#xff1a…
阅读更多...
用动态ip登录账号的风险高不高？

用动态ip登录账号的风险高不高？

使用动态ip登录账号在一定程度上提供了额外的安全保障和匿名性&#xff0c;但与此同时也存在一些风险和风控挑战。本文将解密使用动态ip登录账号的真相&#xff0c;明确安全与风险的并存之道。 1、增强隐私保护&#xff1a; 使用动态ip登录账号可以隐藏您的真实IP地址&#xff…
阅读更多...
21 Spring Boot整合Redis

21 Spring Boot整合Redis

目录 一、Redis简介 二、创建springboot整合redis工程 三、添加依赖 四、配置Yml 五、创建Redis配置类 六、创建Redis工具类&#xff0c;封装Redis的api 七、操作Redis 八、验证 一、Redis简介 简单来说 Redis 就是一个使用 C 语言开发的数据库&#xff0c;不过与传统…
阅读更多...
无涯教程-JavaScript - OR函数

无涯教程-JavaScript - OR函数

描述 如果任何参数为TRUE,则OR函数返回TRUE&#xff1b;如果所有参数为FALSE,则返回FALSE。 语法 OR (logical1, [logical2], ...) 争论 Argument描述Required/Optionallogical1 您要测试的1到255个条件可以是TRUE或FALSE。 您要测试的1到255个条件可以是TRUE或FALSE。 Req…
阅读更多...
JDK API文档地址（中文和英文）

JDK API文档地址（中文和英文）

JDK1.6 JDK 1.6 中文手册 JDK1.8 Java 8 中文版 - 在线API手册 - 码工具 Java 官方文档 |官方教程|Java 官方文档 API中文手册|Java 官方文档参考文档_w3cschool 网上还有很多百度网盘中也有 JDK17 https://doc.qzxdp.cn/jdk/17/zh/api/index.html 英文文档 所有版本 …
阅读更多...
Unity 性能优化之Shader分析处理函数ShaderUtil.HasProceduralInstancing: 深入解析与实用案例

Unity 性能优化之Shader分析处理函数ShaderUtil.HasProceduralInstancing: 深入解析与实用案例

Unity 性能优化之Shader分析处理函数ShaderUtil.HasProceduralInstancing: 深入解析与实用案例 点击封面跳转到Unity国际版下载页面 简介 在Unity中&#xff0c;性能优化是游戏开发过程中非常重要的一环。其中&#xff0c;Shader的优化对于游戏的性能提升起着至关重要的作用。…
阅读更多...
学习视觉SLAM需要会些什么？

学习视觉SLAM需要会些什么？

前言 SLAM是现阶段很多研究生的研究方向&#xff0c;我也是作为一个即将步入视觉SLAM的研究生&#xff0c;网上对于SLAM的介绍很多&#xff0c;但很少有人完整系统的告诉你学习视觉SLAM该有那些基础&#xff0c;那么此贴将告诉你学习SLAM你要有那些方面的基础。 文章目录 前言…
阅读更多...
Java 华为真题-选修课

Java 华为真题-选修课

需求&#xff1a; 现有两门选修课&#xff0c;每门选修课都有一部分学生选修&#xff0c;每个学生都有选修课的成绩&#xff0c;需要你找出同时选修了两门选修课的学生&#xff0c;先按照班级进行划分&#xff0c;班级编号小的先输出&#xff0c;每个班级按照两门选修课成绩和的…
阅读更多...
计算机网络TCP篇之流量控制

计算机网络TCP篇之流量控制

计算机网络TCP篇之流量控制 今天谈一谈我对于tcp流量控制的看法 在网络拓扑中如果发送方节点的发送速率大于接受方节点的接受速率&#xff0c;数据会不断在接受方的缓冲区累积&#xff0c;直到接受方的缓冲区满的时候&#xff0c;发送方继续发送数据&#xff0c;这时候接受方无…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023