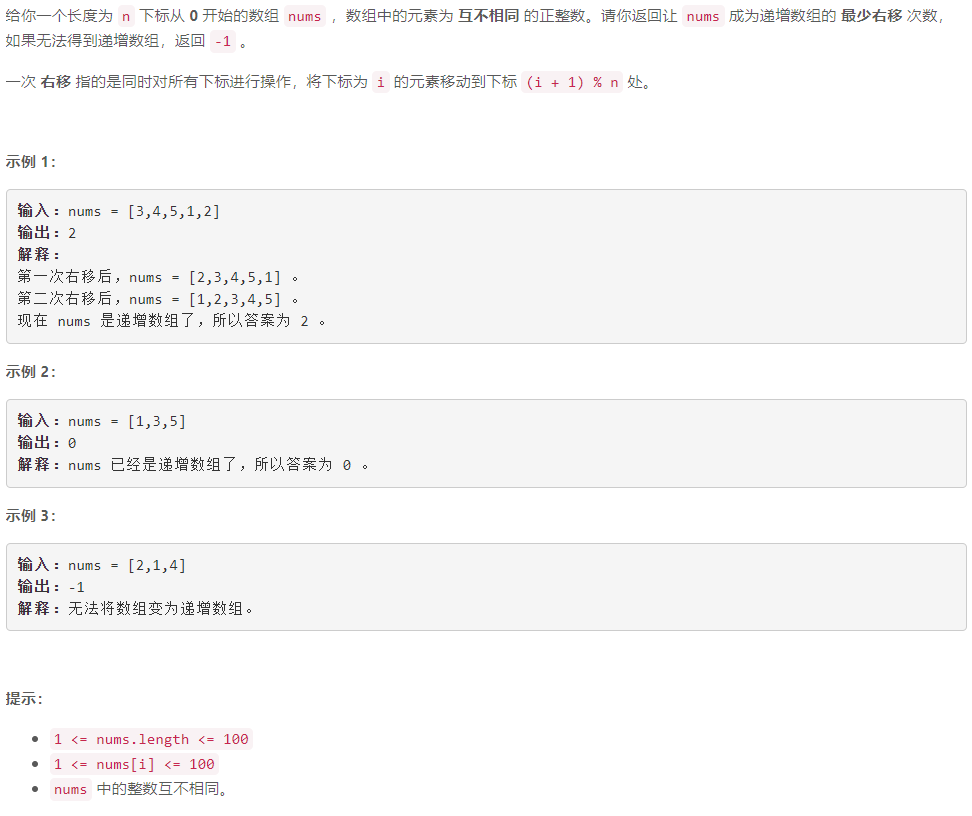
数据范围小直接模拟…

class Solution {
public:int minimumRightShifts(vector<int> &nums) {for (int op = 0; op < nums.size(); op++) {if (is_sorted(nums.begin(), nums.end()))//nums是否已经有序return op;rotate(nums.begin(), prev(nums.end()), nums.end());//右移一次}return -1;}
};

分类讨论：设数组中出现次数最多的数的出现次数为 $mx$

1. 当数组长度为偶数时：若 $mx\le \frac{n}{2}$ 则删除数对后的最小数组长度为 $0$ ，否则删除数对后的最小数组长度为 $mx-(n-mx)$
2. 当数组长度为奇数时：若 $mx\le \lfloor \frac{n}{2}\rfloor$ 则删除数对后的最小数组长度为 $1$ ，否则删除数对后的最小数组长度为 $mx-(n-mx)$

class Solution {
public:int minLengthAfterRemovals(vector<int> &nums) {unordered_map<int, int> cnt;//统计出现次数for (auto x: nums)cnt[x]++;int mx = 0;for (auto &[_, cnt_i]: cnt)mx = max(mx, cnt_i);int n = nums.size();if (n % 2 == 0) return mx <= n / 2 ? 0 : mx - (n - mx);        return mx <= n / 2 ? 1 : mx - (n - mx);}
};

计数+枚举：枚举数组中的坐标 $(p[0],p[1])$ ，枚举可能的与当前坐标距离为 $k$ 的坐标：枚举 $i\in [0,k]$，$(p[0]\wedge i,p[1]\wedge (k-i))$ 即为与当前坐标距离为 $k$ 的坐标，若之前出现过这个坐标则更新答案，在枚举坐标 $(x,y)$ 的过程中记录坐标的出现次数。

class Solution {
public:int countPairs(vector<vector<int>> &coordinates, int k) {map<pair<int, int>, int> cnt;//记录坐标的出现次数int res = 0;for (auto &p: coordinates) {for (int i = 0; i <= k; i++) {int x = p[0] ^ i;int y = p[1] ^ (k - i);auto tmp = make_pair(x, y);auto it = cnt.find(tmp);if (it != cnt.end())//之前出现过坐标(x,y)res += it->second;}cnt[{p[0], p[1]}]++;}return res;}
};

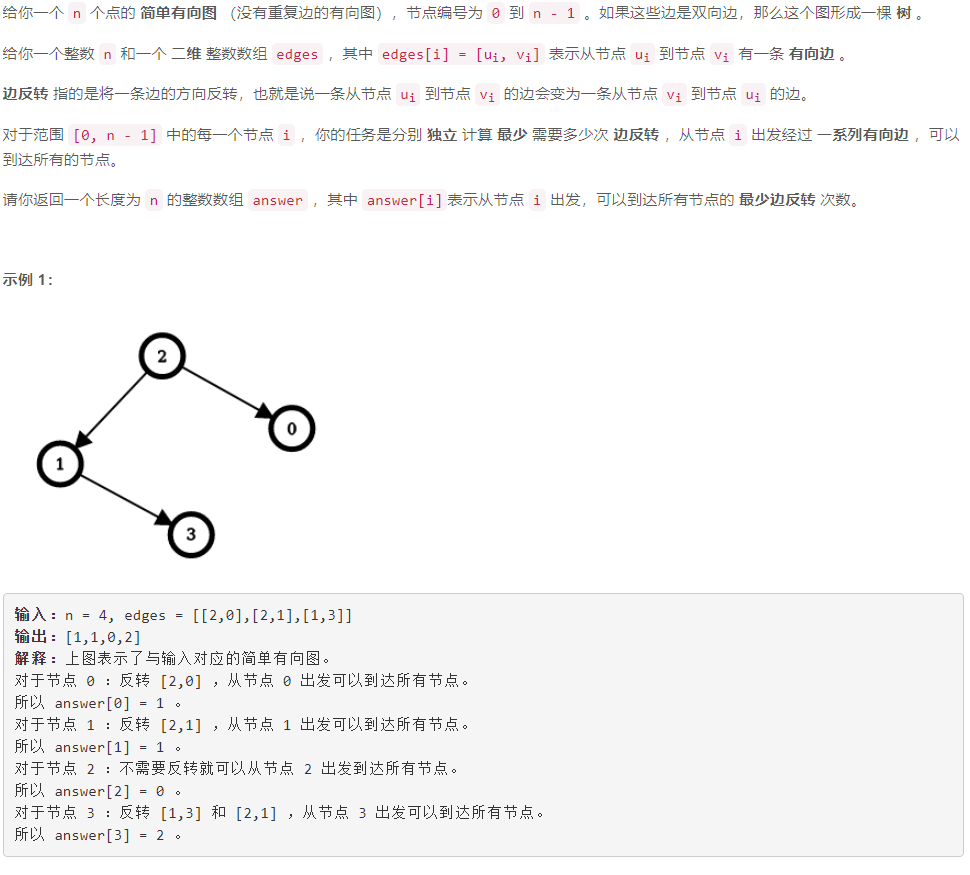
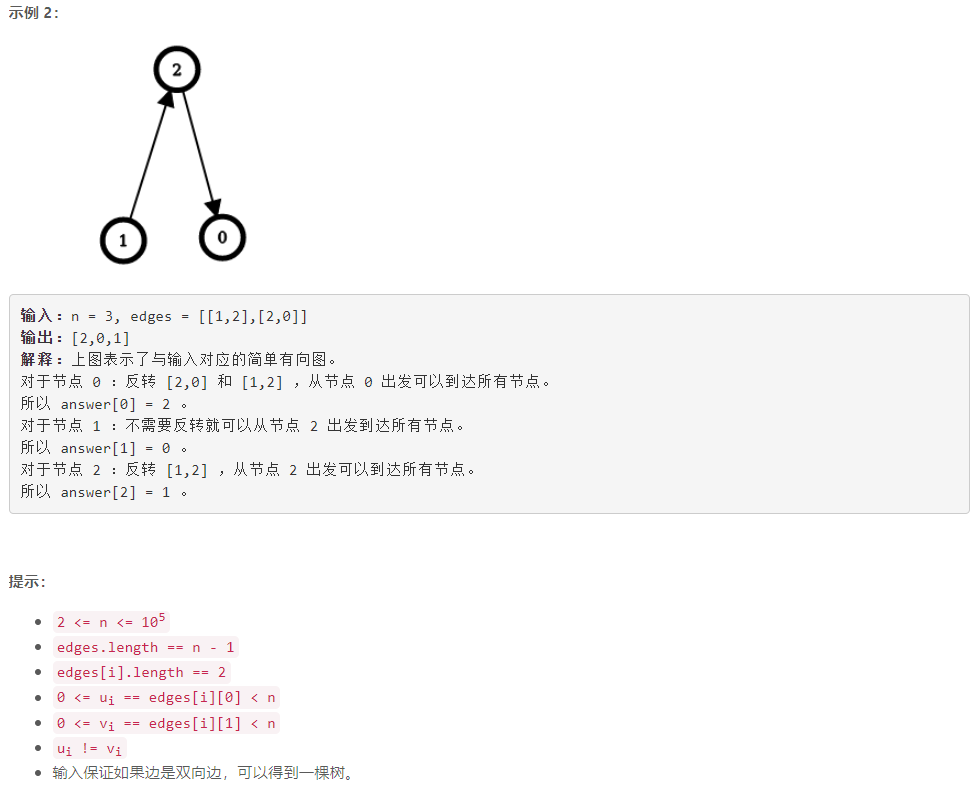
动态规划：首先建无向图，同时记录原始边的方向。不妨设 $0$ 为树根，设 $p[cur]$ 为：使 $cur$ 能够到达以 $cur$ 为根的子树中的所有节点的最少边反转次数。通过 $dfs$ 可以求出 $p$ 数组。然后从 $0$ 开始遍历树中节点 $cur$，遍历过程中维护使 $cur$ 能够到达除以 $cur$ 为根的子树外的所有节点的最少边反转次数 $up\_cost$，则使$cur$ 能够到达所有节点的最少边反转次数有 $res[cur]=p[cur]+up\_cost$

class Solution {
public:vector<int> minEdgeReversals(int n, vector<vector<int>> &edges) {vector<pair<int, int>> e[n];for (auto &ei: edges) {e[ei[0]].emplace_back(ei[1], 0);//0代表正向边e[ei[1]].emplace_back(ei[0], 1);//1代表反向边}int p[n];function<int(int, int)> dfs = [&](int cur, int par) {p[cur] = 0;for (auto &[j, w]: e[cur])if (j != par) {if (w == 1)//(cur,j)这条边需要反转p[cur]++;p[cur] += dfs(j, cur);}return p[cur];};dfs(0, -1);//求p数组vector<int> res(n);function<void(int, int, int)> get = [&](int cur, int par, int up_cost) {res[cur] = p[cur] + up_cost;for (auto &[j, w]: e[cur])if (j != par) {if (w == 0)get(j, cur, res[cur] - p[j] + 1);elseget(j, cur, res[cur] - p[j] - 1);}};get(0, -1, 0);//求答案数组return res;}
};