文章目录
- 1写在前面的话
- 2outlier检测算法
- 2.1获取最大集合(Getting the maximum consistent set)
- 2.2异常值检测
- 2.3估计法线和曲率
- 3实验结果
- 3.1模拟数据
- 3.2真实数据
- 3.3 自己实测结果:
1写在前面的话
论文针对激光点云提出了一种基于平面拟合的去噪算法,该去噪算法寻找邻域内最佳拟合的平面的点云,在此基础上提出了两个去噪算法:一种是基于稳健的z - score,另一种使用马氏类型的稳健距离,并在去噪的基础上提出了法线估计。结果表明:能很好地去除规则物体表面的噪点,并且相对于其他稳健性法线估计算法,文中的法线估计方法更加快,效果更好。
文中算法对于非规则物体,或者远距离噪点效果不好(因为此时并不能取得一个理想的平面)。作者后续的文章也针对这种情况提出了一种与密度相结合的方法,见《AN UNSUPERVISED OUTLIER DETECTION METHOD FOR 3D POINT CLOUD DATA》
2outlier检测算法
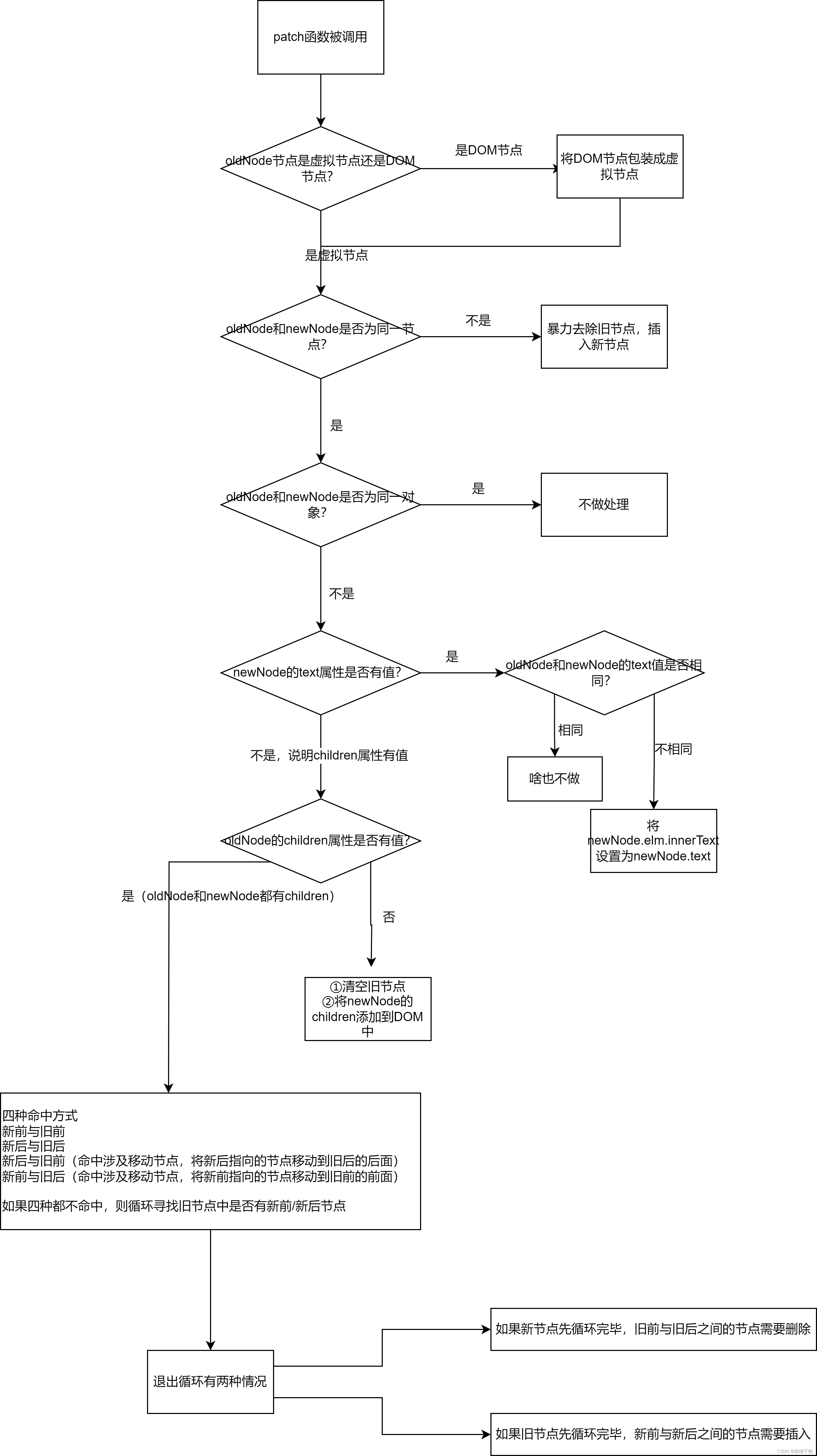
本部分提出了点云数据中的离群点检测和鲁棒显著性特征估计两种算法。算法执行如下图所示的4个顺序任务(图1 )。

我们遵循诊断统计的基本思想,即从识别异常值开始,去除它们,然后以经典的方式拟合剩余的数据[19]。因此,在局部邻域中发现离群点后,我们使用经典的PCA将无异常值的数据拟合平面,并使用最佳拟合平面参数和估计的特征值来估计局部显著性,即法向和曲率。算法有两个目的:( i )点云数据中的离群点检测;( ii )鲁棒的显著性特征估计。
本文提出的两种稳健离群点检测方法分别采用稳健z - score和稳健马氏距离( RMD )。为了识别离群点,该算法将点到平面的正交距离( Orthogonal Distance,OD )和沿法线方向的表面点变化量λ0的思想结合起来。只有局部邻域中最可靠、同一性质且具有最小排序正交距离的大多数近邻点的子集(一个大小为h的子集)被用于拟合平面,并计算各自的λ0值。基于多数形似性质点进行决策是稳健统计中的一个基本思想。h是是一个阈值,一般设置为0.5k。
虽然知道h的大小,但不确定h子集具体对应的点,因此,从h0=3,开始随机选择点,根据蒙特卡洛思想,进行
I t = log ( 1 − P r ) log ( 1 − ( 1 − ϵ ) h 0 ) (1) I_t=\frac{\log \left(1-P_r\right)}{\log \left(1-(1-\epsilon)^{h_0}\right)}\tag{1} It=log(1−(1−ϵ)h0)log(1−Pr)(1)
次迭代,就可以找到h子集对应的点。如果我们设定Pr为期望的概率,本文中设为0.9999. ϵ \epsilon ϵ为异常值概率,根据经验设为0.5.
合理的假设是,在所有的h子集中,沿最小λ0值的平面也具有最大的表面一致性,即沿法线方向的变化最小。理论上,在λ0处达到最大一致性.通过这种方式,我们从具有最小OD的点到拟合平面的最大表面点一致性.我们称之为基于最小距离的最大一致性方法( MCMD:Maximum Consistency with Minimum Distance )。鲁棒的离群点检测和显著性特征估计算法可以概括和整理为以下三个部分。
2.1获取最大集合(Getting the maximum consistent set)
所提出的异常值检测算法受到统计学中鲁棒异常值检测概念的启发:通过搜索大多数数据拟合的模型来检测异常值[15,19]。我们的算法中使用的多数点的子集包括最一致的点。彼此。最大一致集(MCS)可以通过算法1中的以下步骤实现:

2.2异常值检测
z分数:
z i = ∣ p i − p ˉ ∣ StD ( p ) , i = 1 , … , k (2) z_i=\frac{\left|p_i-\bar{p}\right|}{\operatorname{StD}(p)}, \quad i=1, \ldots, k\tag{2} zi=StD(p)∣pi−pˉ∣,i=1,…,k(2)
Median Absolute Deviation (MAD):
MAD = α.median i ∣ p i − median j ( p j ) ∣ (3) \operatorname{MAD}=\underset{i}{\operatorname{\alpha.median}}\left|p_i-\underset{j}{\operatorname{median}}\left(p_j\right)\right|\tag{3} MAD=iα.median pi−jmedian(pj) (3)
α \alpha α=1.4826
综合二者性质,提出稳健性的z分数做为检测异常值的一种方法:
R z i = ∣ p i − median j ( p j ) ∣ MAD ( p ) , i = 1 , … , k (4) Rz_i=\frac{\left|p_i-\underset{j}{\operatorname{median}}\left(p_j\right)\right|}{\operatorname{MAD}(p)}, \quad i=1, \ldots, k\tag{4} Rzi=MAD(p) pi−jmedian(pj) ,i=1,…,k(4)
根据文献15,认为 R z Rz Rz大于2.5为异常值。
此外:马氏距离也是一种检测异常值较为可行的方法:
M D i = ( p i − p ˉ ) T Σ − 1 ( p i − p ˉ ) , i = 1 , … , k (5) \mathrm{MD}_i=\sqrt{\left(p_i-\bar{p}\right)^T \Sigma^{-1}\left(p_i-\bar{p}\right)}, \quad i=1, \ldots, k\tag{5} MDi=(pi−pˉ)TΣ−1(pi−pˉ),i=1,…,k(5)
根据卡方检验,认为 M D i \mathrm{MD}_i MDi大于3.075为异常值。
所提出的算法以两种方式识别 pi 局部邻域中的异常值:(i) 使用 Rz 分数,以及 (ii) 使用稳健马氏距离 (RMD)。这些方法分别称为 MCMD_Z 和 MCMD_MD。算法 2 和 3 总结了两种异常值检测方法:


2.3估计法线和曲率

3实验结果
3.1模拟数据
平面法线估计的稳健性比较:
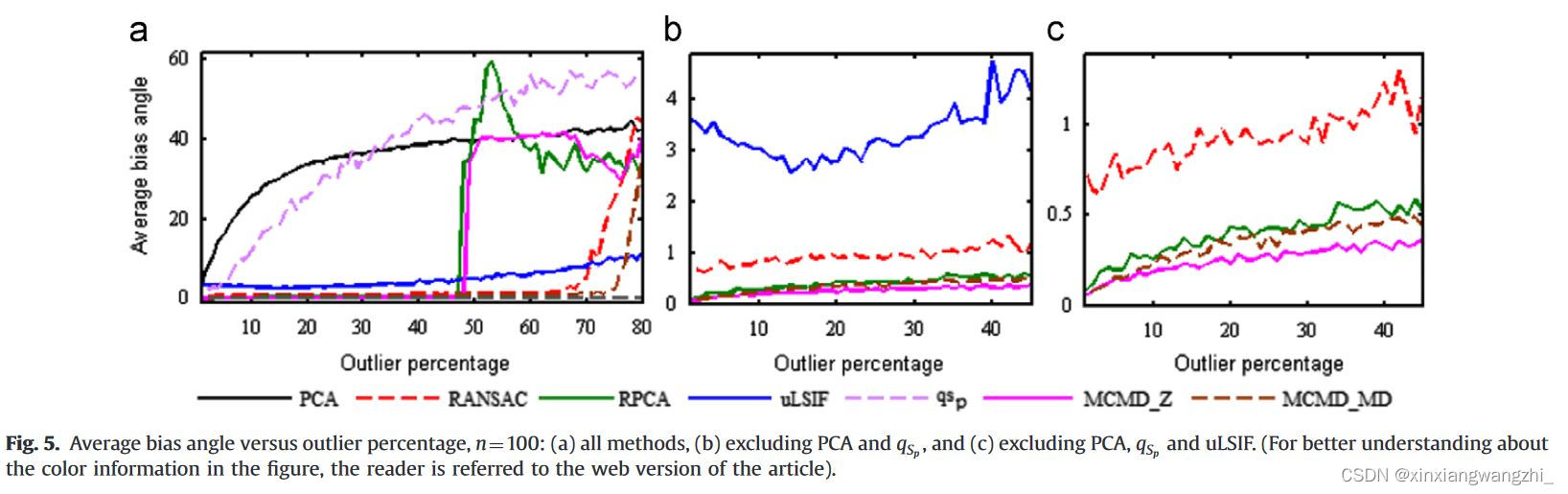
平面法线估计速度:
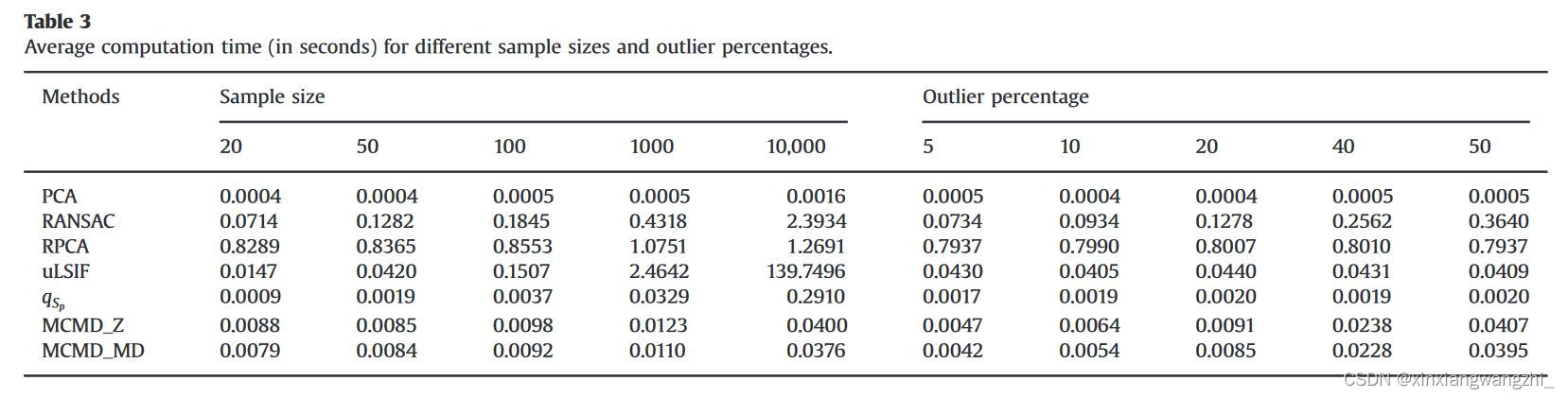
3.2真实数据
去噪结果
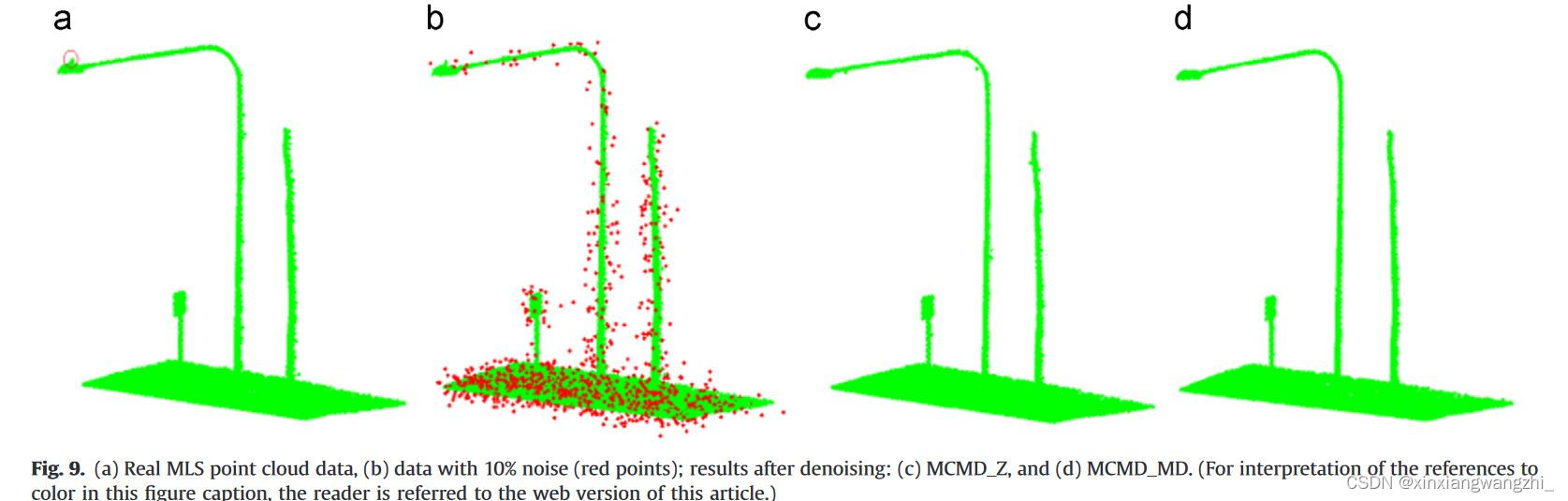
法线拟合结果
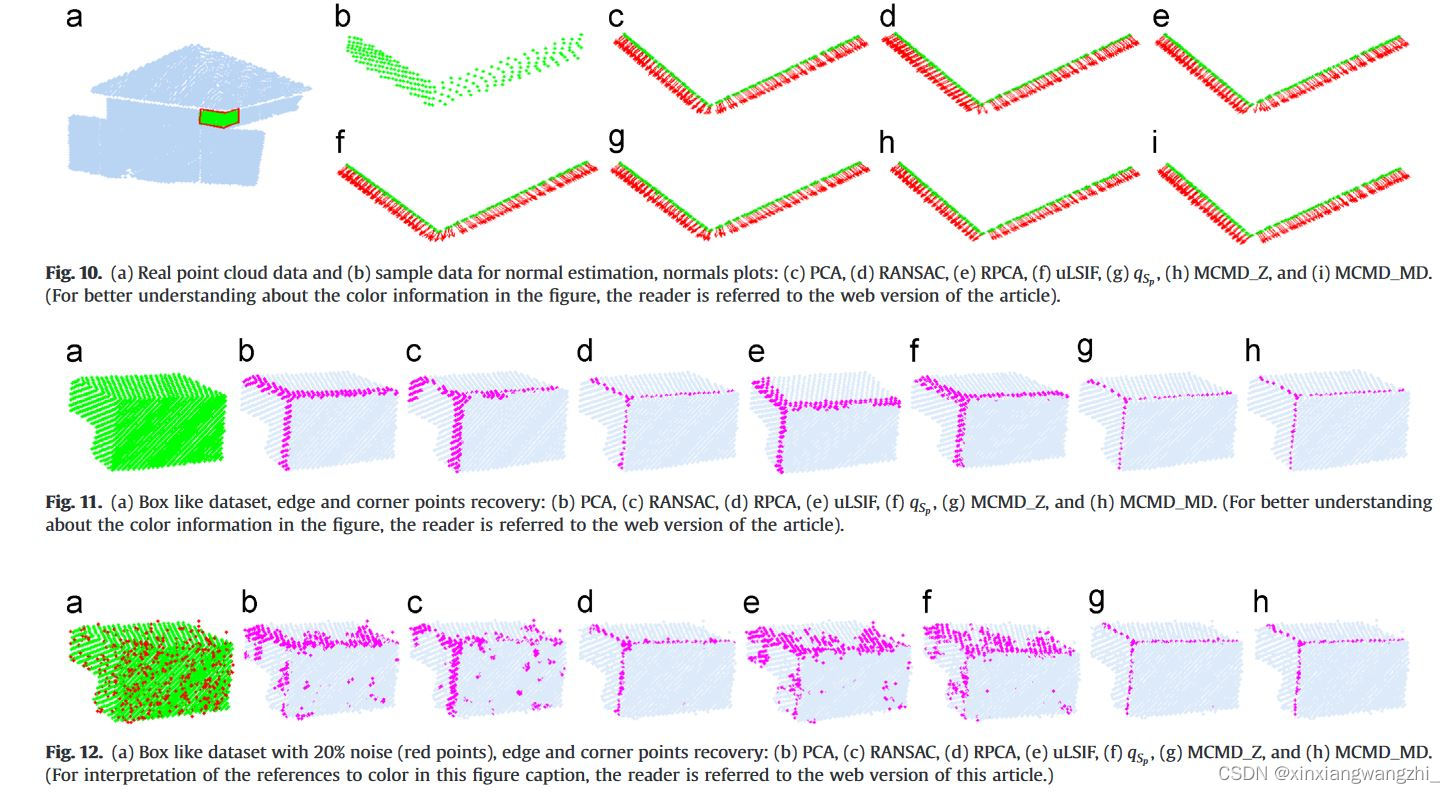
3.3 自己实测结果:
效果还是不错的。
代码我后续可能会放到GitHub上。



《Outlier detection and robust normal-curvature estimation in mobile laser scanning 3D point cloud data》