GAMES103: 基于物理的计算机动画入门
链接:GAMES103
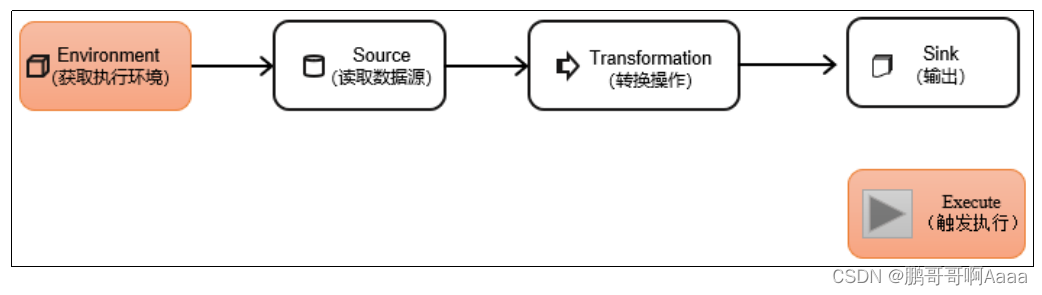
1. 坐标系的划分
在游戏引擎中分为右手和左手坐标系,区分的依据是什么?

上图可以看到如果是左手坐标系,那么所有的物体都在屏幕后面,意味着x,y,z的值都是正的。
2. Vector Norm
向量的长度就是2-Norm,通常使用Vector Norm来评估向量。

3. 投影
投影的计算,可以看到投影的长度只和两个向量有关系。

在游戏引擎中,通常使用投影推出来的Signed Distance,进行碰撞检测的判断。

4. 叉乘
4.1 三角形的拓扑顺序
叉乘决定了两条边计算的方向,因此在录入三角形的时候,也应该注意三角形边的顺序,也叫做拓扑顺序。

4.2 Signed Areas和Barycentric Weights
对于2维中,叉乘引出的重心插值。

对于3维中,可以通过叉乘计算体积,同时叉乘也有相同的规律。

5. 矩阵的分解
5.1 奇异值分解
矩阵的奇异值分解主要的思想:依据于每一个矩阵都可以通过一个正形进行旋转→缩放→旋转的步骤来得到。
因此U和V都是正交矩阵,用于做旋转操作,而D是对角矩阵,来进行缩放,D中的值也称为奇异值。

5.2 特征值分解
注意:在计算机物理学中,主要讨论对称矩阵的特征值分解。
特征值的思想:针对于每一个“轴”的指定缩放。

5.3 LU分解
LU分解的思想:将任何矩阵都能分解为上三角和下三角矩阵的乘积,主要用于求解Ax=b线性方程。

6. 矩阵正定
矩阵正定的通常判定方法:
(1)判定特征值的正负性
(2)使用对角占优的方法判定正定,注意,对角占优能推出正定,但正定不一定对角占优
(3)正定矩阵必定可逆

7. 迭代法求解线性系统
主要目的:使 b − A x [ k ] b-Ax^{[k]} b−Ax[k] 趋近于0,这要求 1 − 1- 1− α \alpha α A M − 1 AM^{-1} AM−1 的谱半径小于1 ,因此M矩阵的不同对应着不同的迭代方法。

可以把线性系统认为是二次优化问题, α \alpha α通常是需要试错的。
迭代法分为:
(1)Jacobi迭代法
(2)Gauss-Seidel迭代法
(3)超松弛(SOR方法)
注意:迭代法求解以后用到会详细说明。
8. 向量的求导
8.1 普通函数对向量x求一阶导
对向量x求一阶导通常用梯度进行表示,意义是最快的增长方向。

8.2 向量函数对向量x求一阶导
向量函数相当用于就是三个函数拼起来的向量,直接求导即可。

上图中Jacobian是雅可比行列式,Divergence是散度,如果将 ▽ \bigtriangledown ▽也看作是一个算子,那么做叉乘会得到Curl,即旋度。
8.3 普通函数对向量x求二阶导
二阶导,因为普通函数对向量求一阶导一定得到的是一个向量,再次求导相当于在做Jacobian。

Hessian(海森矩阵)仅仅是对一阶导的组合,同样的Hessian矩阵的对角叫做Laplacian(拉普拉斯)。
9. 函数对向量参数的泰勒展开

注意:对于向量的二阶泰勒展开是可以判断正定的,这可以带来很多性质,比如极值等。
10. 对弹簧的受力分析
通过链式法则和物理定律我们能推出弹簧受力时的能量、力和能量的海森矩阵。
10.1 针对于x的Norm的求导

10.2 单方向弹簧受力

10.3 双方向弹簧受力
两个方向都有力时,我们将两端的力组合成一个大向量,以相同方式计算即可。