引言

在深度学习过程中总会在代码中遇到优化器.Adam()，在上一篇实现卷积神经网络CNN的代码分析中也提到了优化器的概念,那么优化器如何通俗的理解呢？
个人通俗理解(仅供参考)：为梯度下降法配置的一个的"领航员"，寻找模型最优解又要避免出现局部最优解，使之能快速高效的达到"目标"
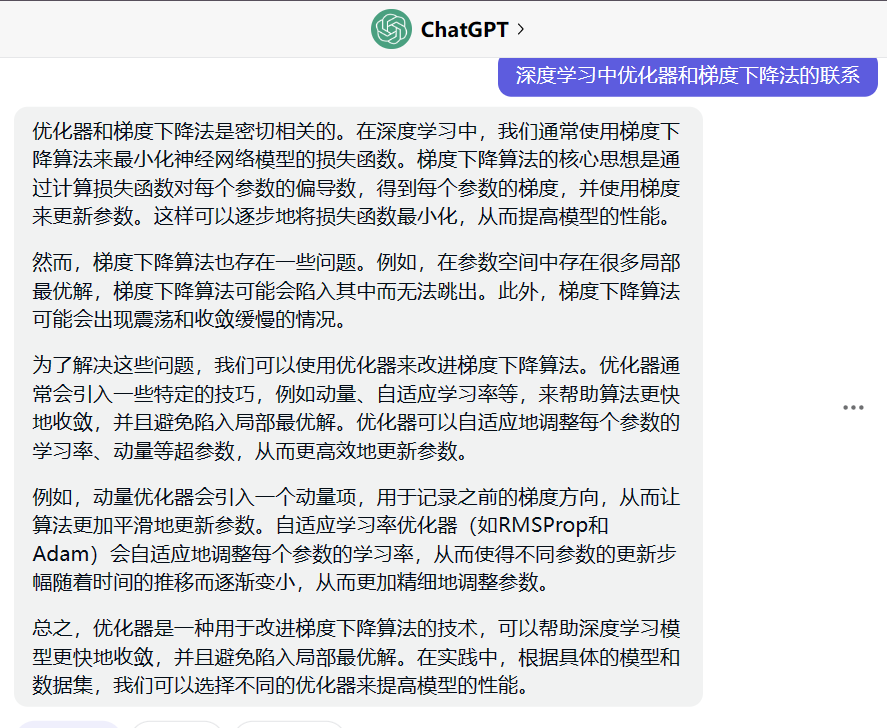
以下为使用chatgpt3.5的回答(仅供参考，还挺全乎，直接给我把本文要介绍的优化器优缺点都总结好了)

优化器在pytorch的调用看这里： pytorch中文文档

介绍顺序:SGD -> SGDM -> NAG ->AdaGrad -> RMSProp -> AdaDelta -> Adam -> Nadam

SGD( 随机梯度下降法)

首先理解优化器要先懂得梯度下降法
个人理解GD系列的通俗数学表达式(仅供参考)
- α表示学习率，ΔT表示梯度（以下三种方法的ΔT代表含义并不一样）
- GD：ΔT会在每输入一个样本就更新一次
- BGD：ΔT会在批量输入数据之后才更新一次(也就是那个batchsize参数)
- SGD：在批量的前提下，随机抽取一个样本更新ΔT
- 以上三个都是在提升参数更新效率的方向上优化，但是都无法克服产生局部震荡，从而只是实现了局部最优解的问题
  $W_{new} = W_{old} - \alpha * ΔT(W_{old})$
更加详尽的解答见：参考资料1
参考资料2

SGDM(带动量的SGD：SGD with momentum)

关于加入动量
- 理解1：为了抑制SGD的震荡，SGDM认为梯度下降过程可以加入惯性。就像下坡的时候，如果发现是陡坡，那就利用惯性跑的快一些，即使重力的作用下也会到底后继续往反方向"攀登一些高度" 参考资料3
SGDM的公式如下（进攻参考）：
- η为动量系数(一般取0.9) V为动量因子
- 其他同SGD是一样的
- 通俗理解原理就是：当更新本次参数的时候，动量因子会根据动量系数保留部分上次梯度，当梯度方向不发生变化那动量因子会加速更新(类比山谷就是陡坡加速到谷底即可)，反之方向相反就要减速最好是直接跳过局部最优解的山谷，前往全部最优解的山谷
  $V_{new} = V_{old}*\eta - \alpha * ΔT(W_{old})$
  $W_{new} = W_{old} + V_{new}$

NAG(Nesterov Accelerated Gradient 加速梯度)

NAG其实是在SGD,SGDM的基础上进一步优化，通过提前"探路"让下降的更加"智能"
NGA中使用"下一步位置"也就是未来的梯度来替换当前位置梯度来完成"探路"，如果下一步位置比当前更陡峭，那就提前"刹车"防止走不到坡底在动量的推动下跳上了另一个高坡从而错过全部最优解，这样就会比纯动量更加保险，就像在动量上加一个限速锁(emm，又不是太准确，上面的η反倒更像限速锁)防止走的太快
那么未来梯度怎么计算呢？
$W_{new} = V_{old}*\eta - \alpha * ΔT(W_{old}) + W_{old}$
在SGD计算公式中，其实alpha * ΔT是一个很小的值，因为梯度下降时候学习率太大也就是步子太大会错过最优点所以一般设置学习率都比较小(即使会导致下降的很慢但是不容易错过最优解呀)，那么这就决定了上面的乘积结果不会太大,我们就近似得到未来位置的W值
$W_{feature} = V_{old}*\eta + W_{old}$
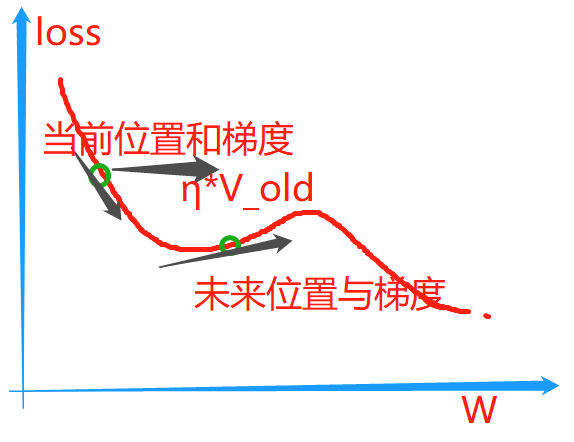
那我们用未来W值再去计算V_new就可以实现在急速的梯度变化的时候提前"适应"，从而提高训练时候的稳定性(W_new依然是动量+W_old)
- 图片仅供参考哈，不一定非常准确相对来说形象一些
  $V_{new} = V_{old}*\eta - \alpha * ΔT(W_{feature})$

关于SGD，SGDM，NAG优化器在Pytorch中已经封装到.SGD函数中了

class torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)[source]

lr：学习率（learning rate），控制每次参数更新的步长。默认值为0.001。
momentum：动量（momentum），加速SGD在相关方向上前进，抑制震荡。常常取值为0.9。若设为0，则为经典的SGD算法。
dampening：阻尼（dampening），用于防止动量的发散(η)。默认值为0。
weight_decay：权重衰减（weight decay），也称权重衰减（weight regularization），用于防止过拟合。默认值为0。
nesterov：采用Nesterov加速梯度法（Nesterov accelerated gradient，NAG）。默认值为False。
最下方将使用上篇CNN代码篇代码替换优化器进行测试，效果可见测试结果参考资料5
参考资料6

Adagrad(Adaptive gradient algorithm)

自适应梯度优化器(自适应学习率优化算法)，优化的是学习率α
- 如参考文章中所说的：深度学习模型中有大量参数(可以看上篇CNN原理介绍的时候就提过全连接神经网络随着层级和神经元的增加参数量成次方倍上升)，但是不是所有的参数更新频率都是一致的，对于更新不频繁的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些；对于更新频繁的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些。
Adagrad引入一个新的概念就是对每个参数进行"缓存"，来判断该参数更新的频率，该值是集合了直到当前点为止的梯度的平方
- Adagrad的数学表达式：（学习率α可以看为全局初始学习率，真正的学习率有α/分母这一部分决定，ε为一个超级小的数来防止分母为0的）
- Adagrad优化器的基本原理根据计算公式解释：如果权重进行了非常大的更新，那么其缓存值也将增加学习率将变得更小，随之权重的更新幅度会随时间而减少。反之如果权重没有进行任何重大更新，那么其缓存值将非常小学习率将提高，从而迫使其进行较大的更新
- 优点：不需要人为的调节学习率，它可以自动调节；对于稀疏的数据它的表现很好，很好地提高了 SGD 的鲁棒性；
- 优点也同样会成为算法的缺点：无论权重过去的梯度如何，由于平方不能为负，因此缓存将始终增加一定的量。因此每个权重的学习率最终都会降低到非常低的值(会到0)以至于训练无法再有效进行(这样就引出了下一个优化器RMSProp)。
- 注：很多参考资料会说明这个cache_{new}是一个对角阵，个人感觉通俗来讲可以暂且将其视为一个变量即可，因为深度学习算法原理计算基本都是矩阵的形式，待理解程度的加深后再做解释
  $cache_{new} =cache_{old} + [ΔT(W_{old})]^2$
  $W_{new} = W_{old} - \frac{\alpha}{\sqrt{cache_{new} + \epsilon}} * ΔT(W_{old})$
接口部分(一般取学习率为0.01)

torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, initial_accumulator_value=0)

RMSProp

RMSprop和下面要介绍的Adadelta 都是为了解决 Adagrad 学习率急剧下降问题的
RMSProp算法修改了AdaGrad的梯度积累为指数加权的移动平均，以及增加一个新参数，衰减率参数γ，防止训练过程提前结束的问题
同类型RMSProp数学表达式如下：(可能有错，进攻理解参考)
$cache_{new} = cache_{old} * \gamma + (1- \gamma) * [ΔT(W_{old})]^2$
$W_{new} = W_{old} - \frac{\alpha}{\sqrt{cache_{new} + \epsilon}} * ΔT(W_{old})$
其实上述公式这样的话是方便理解了，但是我觉得是瑕疵的，因为没有凸显出指数加权移动平均的作用，所以附上下面另一个表达式（下图是下面公式的参考公式）
$E(cache_{new}^2) = E(cache_{old}^2) * \gamma + (1- \gamma) * [ΔT(W_{old})]^2$
$W_{new} = W_{old} - \frac{\alpha}{\sqrt{E(cache_{new}^2) + \epsilon}} * ΔT(W_{old})$

代码部分（γ一般取0.9，学习率η取0.001）

torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)

Adadelta

AdaGrad算法和RMSProp算法都需要指定全局学习率，AdaDelta算法属于是结合了两种算法更新参数的优点
同样通俗数学公式为：
- 从公式可以看出AdaDelta不需要设置一个默认的全局学习率
- 在模型训练的初期和中期，AdaDelta表现很好，加速效果不错，训练速度快。
- 在模型训练的后期，模型会反复地在局部最小值附近抖动。
  $ΔW_{AdaGrad} = - \frac{\alpha}{\sqrt{cache_{new} + \epsilon}} * ΔT(W_{old})$
  $ΔW_{RMSprop} = - \frac{\alpha}{\sqrt{E(cache_{new}^2) + \epsilon}} * ΔT(W_{old})$
  $\frac{ΔW_{AdaGrad}}{ΔW_{RMSprop}}$
  $W_{new} = W_{old} + ΔW$
代码部分（γ一般设置为0.9）

torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)

Adam(Adaptive Moment Estimation)

前面SGD-M在SGD基础上增加了一阶动量，AdaGrad和AdaDelta在SGD基础上增加了二阶动量(其实就是那个平方项，很多参考资料称之为二阶动量)，那么把一阶动量和二阶动量都用起来就是Adam的构成了，即：Adaptive（Adadelta, RMSProp,Adagrad） + Momentum。
首先我们计算动量部分：（与之前的V_new表达式只是把学习率α换成了(1-β)）
$m_{new} = \beta1 * m_{old} - (1 - \beta) * ΔT(W_{old})$
接下来二阶动量(参数缓存)部分，结构一毛一样
$cache_{new} = cache_{old} * \beta2 + (1- \beta2) * [ΔT(W_{old})]^2$
$W_{new} = W_{old} - \frac{\alpha}{\sqrt{cache_{new} + \epsilon}} * m_{new}$
Adam通过计算动量来执行梯度的累积，而且我们还通过使用缓存不断地改变学习率。所以在神经网络中相对比较常用甚至是无脑选的感觉，Adam通常被认为对超参数的选择相当鲁棒，尽管学习率有时需要从建议的默认修改。
在Adam的论文中，建议的参数beta_1为0.9，beta_2为0.99，epsilon为1e-08 .
补：其实真实场景是下图的方式，初始值都为0，需要进行修正后参数才可以使用

代码部分（一般 β1 ＝ 0.9，β2 ＝ 0.999，ϵ ＝ 10e−8）

torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)

Nadam(Nesterov-accelerated adaptive moment estimation)

Adam是融合了动量和缓存，但是还有一个NAG思想没用上，那么再融合NAG加速就是Nadma了，但是NAG思想是用下一个预测点来探路，但是在Nadam中并未使用而是在当前位置对当前梯度方向做两次更新
参考上面Aadm的图示，看下图比对理解即可(由于个人理解也有点不太确定，所以仅供参考待后面理解更深再做修改解释)

代码部分(该优化器貌似没有内置，仅供参考此处待以后如果用到再详细介绍)

torch.optim.NAdam(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, momentum_decay=0.004)

参考资料中都有一个各个优化器的动画图，这里也贴上(仅供参考)

优化器1
优化器2

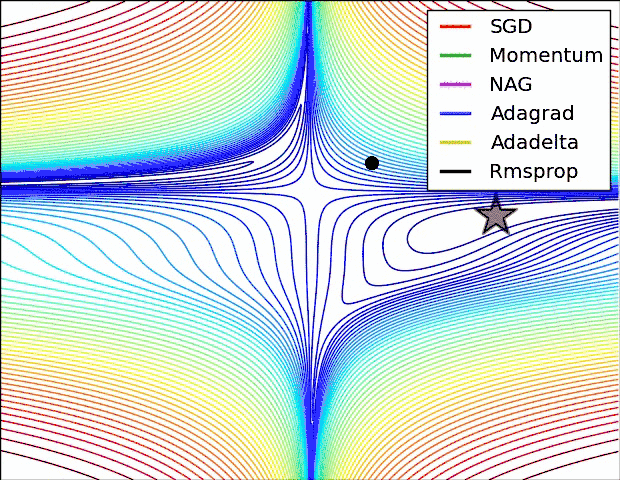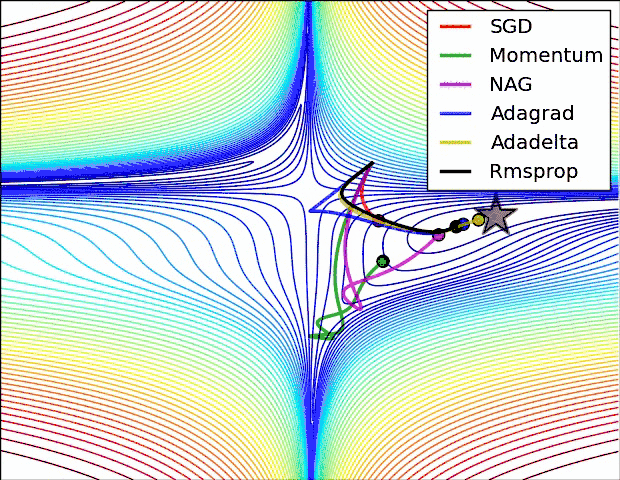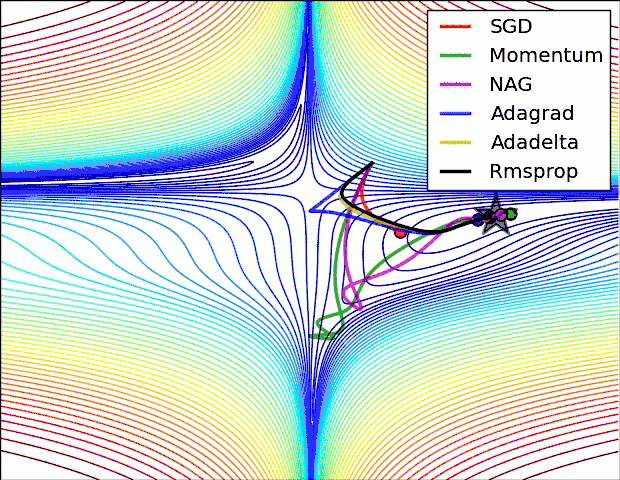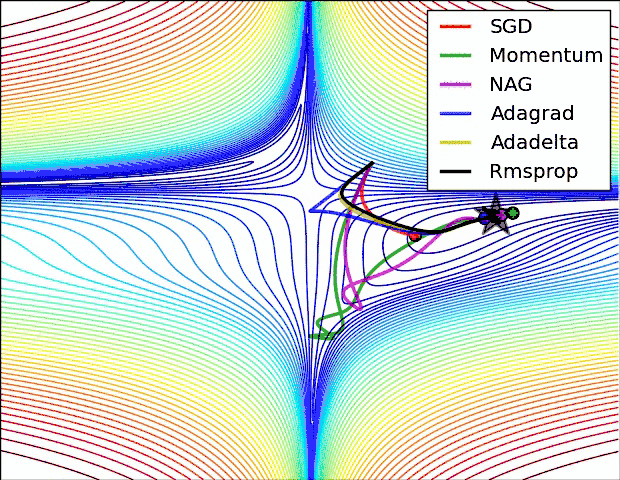
下面是学习时候见到的一个使用python实现各种优化器文章，代码个人并未测试，仅供参考
使用python实现各个优化器

结尾：

首先：关于本文中优化器的数学表达式，分成两种，一种是通俗形式(经供参考可能有错误)，另一种是各种版本的数学表达式，相对比较抽象，也很费解，文中我会简单说明一下注意甄别，个人感觉由于实际使用中是调用优化器函数，要理解的是1：各个优化器优化思想 2：懂得优化器函数中超参数在数学表达式的意义可以调参即可，用来表达优化器思想的数学式子可以是千变万化的
文中有错误的地方欢迎指正，共同进步
文中代码部分部分有验证，验证详情待资源文件，未验证的还请斟酌食用
- GITHUB资源地址
关于实际测试的文件待更新…(资源需要审核，其中后几个优化器我的pytorch版本太低并不支持，与python版本要匹配所以未测试出结果，有兴趣可以自行安装后测试)