LeetCode 518.零钱兑换II 动态规划 + 完全背包 + 组合数

给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。题目数据保证结果符合 32 位带符号整数。

示例 1：

输入：amount = 5, coins = [1, 2, 5]
输出：4
解释：有四种方式可以凑成总金额：
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

示例 2：

输入：amount = 3, coins = [2]
输出：0
解释：只用面额 2 的硬币不能凑成总金额 3 。

示例 3：

输入：amount = 10, coins = [10] 
输出：1

>>思路和分析

① 钱币数量不限，可以知道这是一个完全背包的问题；
② 与纯完全背包式凑成背包最大价值是多少，而本题是要求凑成总金额的物品组合个数！

注意题目描述中是凑成总金额的硬币组合数，为什么强调是组合数呢？

例如示例一：

5 = 2 + 2 + 1

5 = 2 + 1 + 2

这是一种组合，都是 2 2 1。如果问的是排列数，上面就是两种排列了。

注意：组合不强调元素之间的顺序，排列强调元素之间的顺序

>>动规五部曲

1.确定dp数组以及下标的含义

dp[j] : 凑成总金额 j 的货币组合数为 dp[j]

2.确定递推公式

dp[j] 就是所有的 dp[j - coins[i]] （考虑 coins[i] 的情况）相加
所以递推公式：dp[j] += dp[j - coins[i]];

0-1背包题目有这篇LeetCode 494.目标和中讲解了，求装满背包有几种方法，公式都是：

dp[j] += dp[j - nums[i]];

3.dp数组初始化

dp[0] = 1，这是递归公式的基础；若dp[0] = 0的话，后面所有推导出来的值都是0了

下标非0的dp[j]初始化为0，这样累计加dp[j - coins[i]]的时候才不会影响真正的 dp[j]

dp[0] = 1 还说明了一种情况：如果正好选了coins[i]后，也就是 j - coins[i] == 0的情况表示这个硬币刚好能选，此时 dp[0] 为1 表示只选coins[i]存在这样的一种选法

4.确定遍历顺序

方式一：先遍历物品再遍历背包
方式二：先遍历背包再遍历物品

在纯完全背包中，先遍历物品再遍历背包，还是先遍历背包再遍历物品，两者都可以！

本题就不行了！因为纯完全背包求得装满背包的最大价值是多少，和凑成总和的元素有没有顺序是没有关系的，即：有顺序也行，没顺序也行！

但在本题中要求凑合总和的组合数，元素之间明确要求没有顺序的。所以只能是方式一这种遍历顺序，那为什么不能是方式二呢？

对于方式一在完全背包中：外层for 循环遍历物品（钱币），内层for遍历背包（金钱总额）的情况

for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];}
}

假设：coins[0] = 1,coins[1] = 5

那么就是先把1加入计算，再把5加入计算，得到的只有{1,5}这种情况，是不会出现{5,1}这种情况的，所以这种遍历顺序中dp[j]里计算的是组合数！

对于方式二在完全背包中：外层for遍历背包（金钱总额），内层for 循环遍历物品（钱币）的情况

for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.size(); i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];}
}

背包容量的每一个值，都是经过1 和 5的计算，包含了 {1,5} 和 {5,1}两种情况。此时dp[j]里算出来的就是排列数!

5.举例推导dp数组

输入：amount = 5,coins = [1,2,5],dp状态图如下：

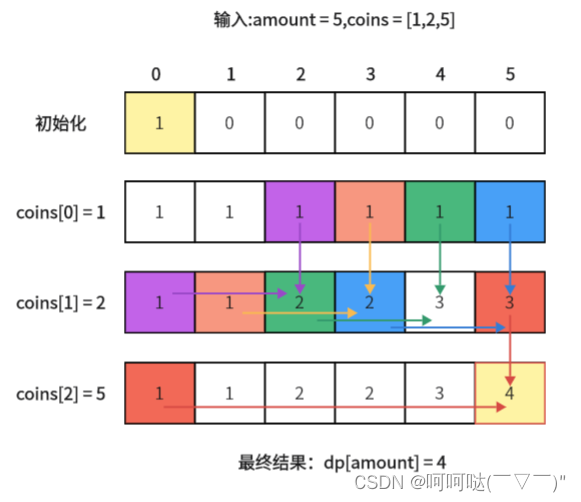
dp[amout]为最终结果

class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);dp[0] = 1;for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包dp[j] += dp[j - coins[i]];}}return dp[amount];}
};