原文链接：https://arxiv.org/abs/2308.09905

1. 引言

  多目标跟踪通常分为两阶段的检测后跟踪（TBD）和一阶段的联合检测跟踪（JDT）。TBD对单帧进行目标检测后，使用跟踪器跨帧关联相同物体。使用的跟踪器包括使用卡尔曼滤波器的基于运动的跟踪、使用重新识别技术关联物体、基于图的跟踪器（将关联过程建模为最小代价流问题）。
  JDT方法统一处理跟踪与检测，可分为3类：基于查询的跟踪器（使用隐式的独特查询，强制查询跟踪相同物体）、基于偏移量的跟踪器（使用运动特征估计运动偏移量）和基于轨迹的跟踪器（利用时空信息处理严重的物体遮挡问题）。
  但多数TBD和JDT方法存在下列问题：

1. 全局或局部的不一致性：TBD对检测和跟踪分开的训练过程导致全局不一致性，而JDT也将检测和跟踪置于不同分支或模块，并未完全解决不一致性。
2. 鲁棒性和模型复杂度的平衡是次优的：TBD简单，但检测波动影响性能；JDT鲁棒，但损害了检测精度。
3. 同一视频内不同场景的不灵活性：在统一的设置下处理视频，而没有将策略自适应地应用于不同场景下。

  本文提出DiffusionTrack，建立了新的从噪声到跟踪的范式。该方法直接从相邻帧内的一组随机边界框对形成目标关联，如图所示。细化边界框对的坐标，使其覆盖两帧内的同一物体，从而在统一模型下隐式地同时进行检测与跟踪。

3. 方法

3.1 准备知识

  多目标跟踪的目标是获取一组按时间排序的输入目标对$(X_t,B_t,C_t)$，其中$X_t$是$t$时刻的输入图像，$B_t$和$C_t$是$t$时刻边界框和类别标签的集合。$B_t$的元素$B_t^i=(c_x^i,c_y^i,w_i,h_i)$，其中$i$为物体的标识编号。当$X_t$中第$i$号物体不存在或未被检测到时，$B_t^i=\varnothing$。
  扩散模型通常利用两个马尔科夫链，即为图像添加噪声的前向链和从噪声提炼出图像的逆向链。给定数据分布$x_0\sim q(x_0)$并定义方差序列${\beta }_1,{\beta }_2,\cdots ,{\beta }_T$，前向过程被定义为$$p(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)$$给定$x_0$，通过采样高斯向量$ϵ\sim \mathcal{N}(0,I)$，按照下式即可得到$x_t$的样本：$$x_t=\sqrt{{\bar{\alpha }}_t}{x}_0+(1-{\bar{\alpha }}_t){ϵ}_t$$其中${\bar{\alpha }}_t={\prod }_{s=0}^t(1-{\beta }_s)$。训练时，网格会根据不同时刻的$x_t$预测$x_0$。推断时，从随机噪声$x_T$开始并迭代进行逆向过程以获得$x_0$。

3.2 DiffusionTrack

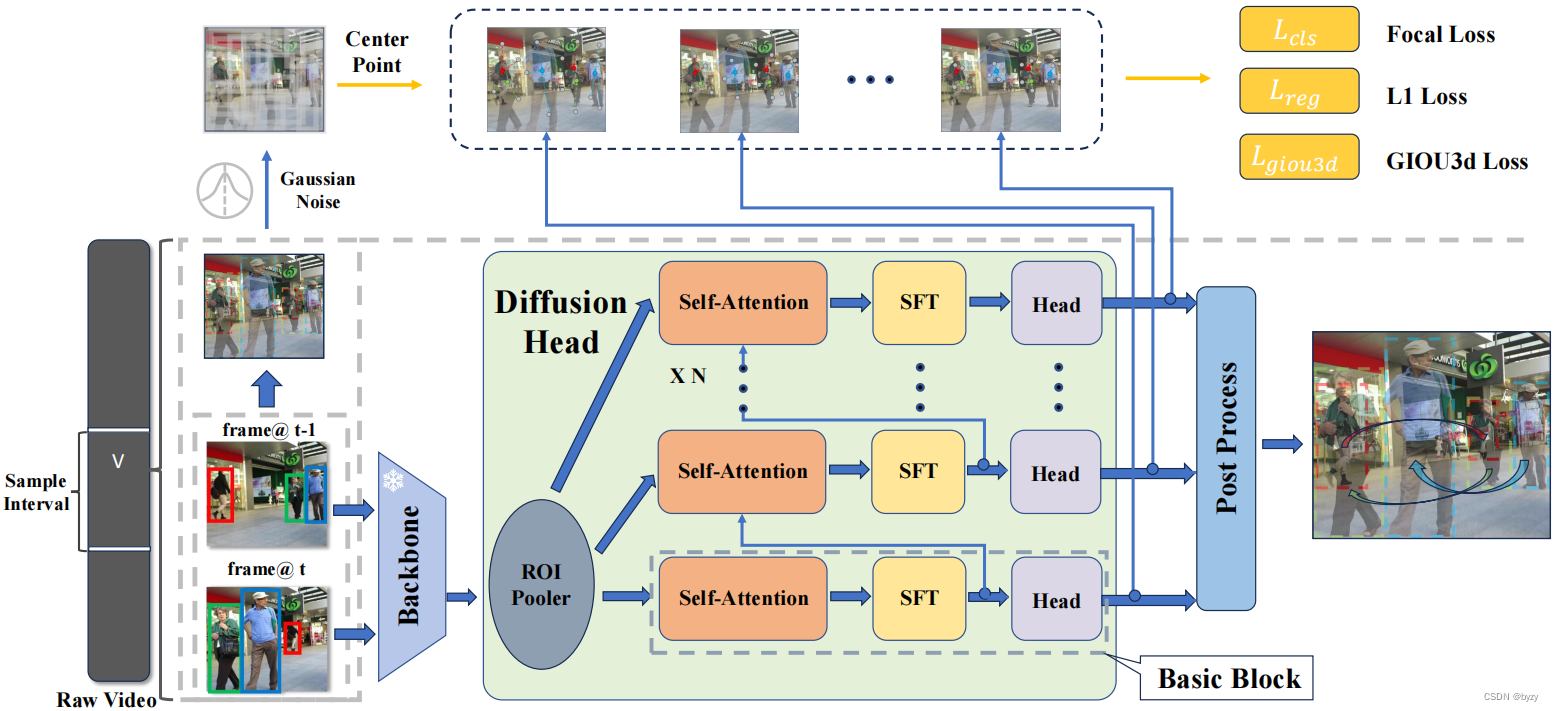
  网络结构如图所示，包含特征提取主干和数据关联去噪头（扩散头），前者运行一次，以提取深度相邻两帧$(X_{t-1},X_t)$的特征表达，后者将特征作为条件，逐步从带噪声的边界框对中提炼出预测的关联边界框对。数据样本为边界框对的集合$z_0=(B_{t-1},B_t)\in {\mathbb{R}}^{N\times 8}$。神经网络 f θ ( z s , s , X t − 1 , X t ) , s ∈ { 0 , 1 , ⋯ , T } f_\theta(z_s,s,X_{t-1},X_t),s\in\{0,1,\cdots,T\} fθ​(zs​,s,Xt−1​,Xt​),s∈{0,1,⋯,T}被训练为从$z_s$预测$z_0$，并以相邻两帧图像为条件。相应的类别标签$(C_{t-1},C_t)$和关联置信度分数$S$也同时被预测。如果$X_{t-1}=X_t$，则多目标跟踪任务退化为目标检测任务。
  主干使用YOLOX+FPN。
  扩散头将提案框用于从特征图中裁剪RoI特征，并将其输入不同块以获取边界框回归值、分类结果和关联置信度分数。此外，还为扩散头的每个块添加了一个时空融合模块（STF）和关联分数头。
  时空融合模块使边界框对能交换时间信息以保证数据关联的完整性。给定RoI特征$f_{roi}^{t-1},f_{roi}^t\in {\mathbb{R}}^{N\times R\times d}$和当前块的自注意力输出查询$q_{pro}^{t-1},q_{pro}^t\in {\mathbb{R}}^{N\times d}$，使用线性投影和批矩阵乘法获得物体查询$q^{t-1},q^t\in {\mathbb{R}}^{N\times d}$：
$$\begin{array}{rl}[P_1^i;P_2^i]& =Linear1(q_{pro}^i),P_1^i,P_2^i\in {\mathbb{R}}^{N\times Cd}\\ \mathbf{feat}& =[f_{roi}^i,f_{roi}^{2t-1-i}],\mathbf{feat}\in {\mathbb{R}}^{N\times 2R\times d}\\ \mathbf{feat}& =\mathtt{Bmm}(\mathbf{feat},P_1^i.\mathtt{view}(N,d,C))\\ \mathbf{feat}& =\mathtt{Bmm}(\mathbf{feat},P_2^i.\mathtt{view}(N,C,d))\\ q_i& =Linear2(\mathbf{feat}.\mathtt{flatten}(1)),q^i\in {\mathbb{R}}^{N\times d}\end{array}$$其中$[\cdot ,\cdot ]$表示拼接，$[\cdot ;\cdot ]$表示划分， i ∈ { t − 1 , t } i\in\{t-1,t\} i∈{t−1,t}。
  关联分数头将边界框对的融合特征输入线性层，用于获取数据关联的置信度分数。该分数用于在后续的NMS后处理环节中，确定输出的边界框对是否属于同一物体。

3.3 模型训练和推断

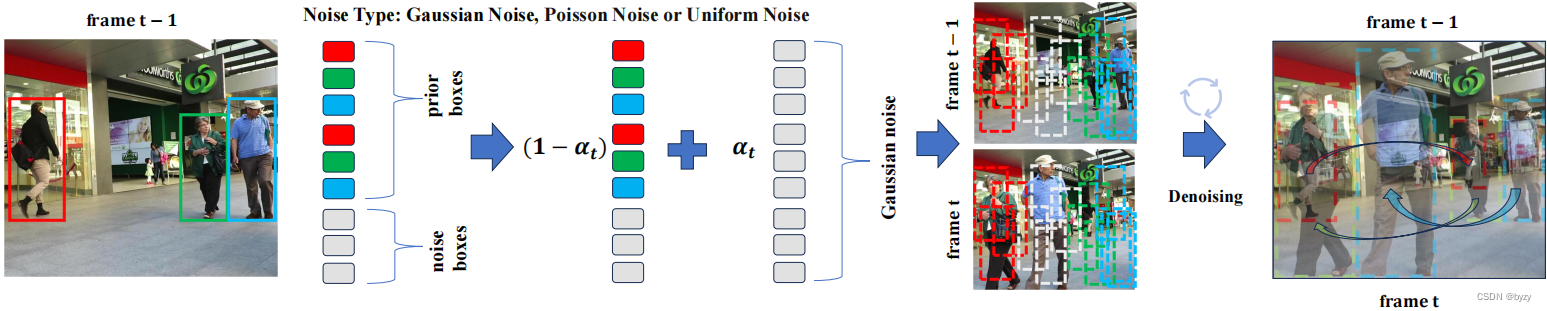
  训练时，随机从视频中采样两帧（帧间隔为5），并填充边界框使其数量为$N_{train}$。然后，${\alpha }_t$使用单调递减余弦调度，并为真实边界框添加高斯噪声。最后，使用去噪过程从带噪声的边界框获取关联边界框对。此外，还设计了一个基准方案，即仅对当前帧添加噪声，并基于过去帧的边界框进行去噪，以证明同时对两帧进行破坏的必要性。
  损失函数：使用GIoU的扩展3D GIoU。对用匈牙利算法获取的匹配集$M$中的匹配对$(T_d,T_{gt})$，记其分类分数、边界框和关联置信度分数为$(C_d^{t-1},C_d^t),(B_d^{t-1},B_d^t)$和$S_d$。损失函数如下：$$\begin{gathered} {\mathcal{L}}_{cls}(T_d,T_{gt})=\sum _{i=t-1}^t{\mathcal{L}}_{cls}(\sqrt{C_d^i\times S_d},C_{gt}^i) \\ {\mathcal{L}}_{reg}(T_d,T_{gt})=\sum _{i=t-1}^t{\mathcal{L}}_{reg}(B_d^i,B_{gt}^i) \\ {L}_{det}=\frac{1}{N_{pos}}\sum _{(T_d,T_{gt})\in M}{\lambda }_1{\mathcal{L}}_{cls}(T_d,T_{gt})+{\lambda }_2{\mathcal{L}}_{reg}(T_d,T_{gt})+{\lambda }_3(1-{\mathtt{GIoU}}_{3D}(T_d,T_{gt})) \end{gathered}$$其中$T_d$和$T_{gt}$分别包含相邻两帧内对同一目标的估计结果和真实边界框。$N_{pos}$为前景目标数。${\mathcal{L}}_{cls}$为focal损失，${\mathcal{L}}_{reg}$为L1损失。
  如下图所示为推断过程。与检测不同，由于已知过去帧的估计结果，可由过去帧的边界框生成$N_{test}$个初始的带噪声边界框。基准方案中，重复已有边界框而非添加随机边界框，并只对当前帧添加噪声。得到关联结果以后，使用IoU衡量相似性并连接物体轨迹。为处理潜在的遮挡，使用卡尔曼滤波器重新关联丢失的物体。

4. 实验

4.1 设置

  实施细节：使用YOLOX检测器+DiffusionTrack。训练分为两阶段：首先以检测任务进行训练，然后以跟踪任务训练。

4.2 特性

  DiffusionTrack有动态边界框、逐步细化的特性以及对检测扰动的鲁棒性。
  动态边界框和逐步细化：一旦训练好模型，推断时，DiffusionTrack的边界框数量和采样步数均可修改。因此可以在不重新训练的情况下实现性能和精度的平衡。
  对检测扰动的鲁棒性：过去的所有方法几乎都对检测扰动敏感，这在自动驾驶中存在安全问题。实验表明DiffusionTrack几乎不受检测扰动的影响。

4.3 消融研究

  基于图3，本文研究各部分的影响。
  先验信息的比例：由于跟踪任务有前一帧物体的先验，可通过复制已有边界框的数量来控制先验信息的比例。实验表明合适的比例能提高性能。
  边界框填充策略：填充服从高斯分布的随机边界框的性能优于服从其余分布的随机边界框、图像大小的边界框和复制已有边界框。
  扰动调度：为处理复杂情况，需要调整${\alpha }_t$。例如，当物体非线性运动时，需要增大${\alpha }_t$。扰动调度可用$t$建模，表示为$t=\max (999,\min (0,1000f(x)))$，其中$x$为跨越两帧物体的平均百分比，$f$为扰动调度函数。实验表明最优的调度为对数调度，即$f(x)=\frac{\log (x+1)}{\log 2}$。
  效率比较：更多的细化步骤能提高性能，但也会降低速度。

4.4 与SotA比较

  本文的方法能在MOT17、MOT20和Dancetrack数据集上达到一阶段方法的SotA水平。
  基准方案在MOT17上的性能相似，但在其余数据集上下降严重。这是因为其只学习了给定$t-1$时刻特征的情况下，$B_{t-1}$和$B_t$之间的坐标回归，而不能处理非线性物体运动。本文猜测扩散过程属于一种特殊的数据增强方式，能使DiffusionTrack区分不同目标。