文章前言:如果有小白同学还是对于二叉树不太清楚,作者推荐:
二叉树的初步认识_加瓦不加班的博客-CSDN博客


后序遍历求解
public int minDepth(TreeNode node) {if (node == null) {return 0;}int d1 = minDepth(node.left);int d2 = minDepth(node.right);//不应该再把为 null 子树的深度 0 参与最小值比较//第一种写法://if (d1 == 0 || d2 == 0) {// return d1 + d2 + 1;//}//第二种写法:if(d1==0){//当右子树为NULLreturn d2+1;//返回左子树深度+1}if(d2==0){//当左子树为NULLreturn d1+1;//返回右子树深度+1}//只有两边子树都不为null时return Integer.min(d1, d2) + 1;
}相较于求最大深度,应当考虑:
当右子树为 null,应当返回左子树深度加一
当左子树为 null,应当返回右子树深度加一
上面两种情况满足时,不应该再把为 null 子树的深度 0 参与最小值比较,例如这样
1/2-
正确深度为 2,若把为 null 的右子树的深度 0 考虑进来,会得到错误结果 1
1\3\4-
正确深度为 3,若把为 null 的左子树的深度 0 考虑进来,会得到错误结果 1
层序遍历求解
遇到的第一个叶子节点所在层就是最小深度
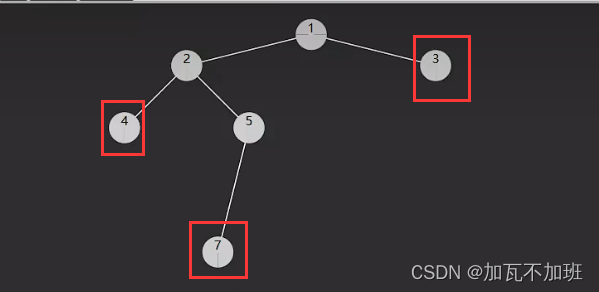
例如,下面的树遇到的第一个叶子节点 3 所在的层就是最小深度,其他 4,7 等叶子节点深度更深,也更晚遇到
1/ \ 2 3/ \4 5 /7 代码:
public int minDepth(TreeNode root) {if(root == null) {return 0;}Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int level = 0;while (!queue.isEmpty()) {level++;int size = queue.size();for (int i = 0; i < size; i++) {TreeNode node = queue.poll();//找寻叶子节点:左右孩子都是Null就是叶子节点if (node.left == null && node.right == null) {return level;}if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}}}return level;
}效率会高于之前后序遍历解法,因为找到第一个叶子节点后,就无需后续的层序遍历了