废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【子结构】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公司+最近一年+出现频率排序,由高到低的去牛客TOP101去找,只有两个地方都出现过才做这道题(CodeTop本身汇聚了LeetCode的来源),确保刷的题都是高频要面试考的题。
明确目标题后,附上题目链接,后期可以依据解题思路反复快速练习,题目按照题干的基本数据结构分类,且每个分类的第一篇必定是对基础数据结构的介绍。
树的子结构【MID】
双重递归,前所未有的体验
题干
直接粘题干和用例

解题思路
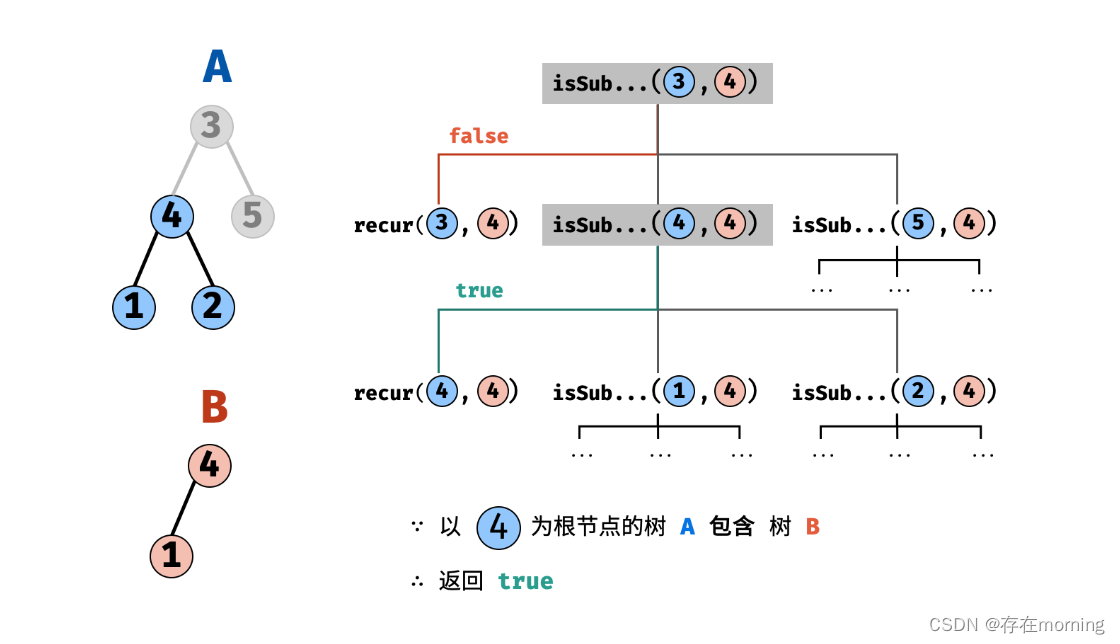
原题解地址,若树 B 是树 A 的子结构,则子结构的根节点可能为树 A 的任意一个节点。因此,判断树 B 是否是树 A 的子结构,需完成以下两步工作:
- 先序遍历树 A 中的每个节点 node ;(对应函数
isSubStructure(A, B)) - 判断树 A 中以 node 为根节点的子树是否包含树 B 。(
对应函数 recur(A, B))
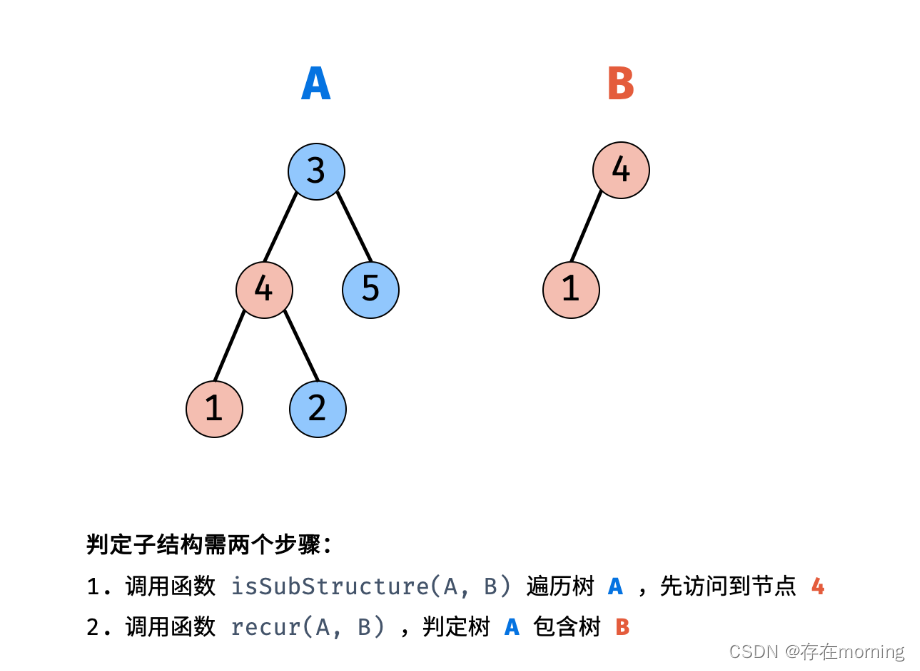
树 A 的根节点记作 节点 A ,树 B 的根节点称为 节点 B 。
recur(A, B) 函数:
终止条件:
- 当节点 B 为空:说明树 B 已匹配完成(越过叶子节点),因此返回 true ;
- 当节点 A 为空:说明已经越过树 A 的叶节点,即匹配失败,返回 false;
- 当节点 A 和 B 的值不同:说明匹配失败,返回 false ;
返回值:
- 判断 A 和 B 的 左子节点 是否相等,即
recur(A.left, B.left); - 判断 A 和 B 的 右子节点 是否相等,即
recur(A.right, B.right);
isSubStructure(A, B) 函数:
特例处理: 当 树 A 为空 或 树 B 为空 时,直接返回 false;
返回值: 若树 B 是树 A 的子结构,则必满足以下三种情况之一,因此用或 || 连接;
- 以 节点 A 为根节点的子树 包含树 B ,对应 recur(A, B);
- 树 B 是 树 A 左子树 的子结构,对应
isSubStructure(A.left, B); - 树 B 是 树 A 右子树 的子结构,对应
isSubStructure(A.right, B);
代码实现
给出代码实现基本档案
基本数据结构:二叉树
辅助数据结构:无
算法:递归
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param n int整型 the n* @return int整型*/public boolean isSubStructure(TreeNode A, TreeNode B) {// 1 如果A树或B树为空,则匹配失败if (A == null || B == null) {return false;}// 2 A的当前节点包含B,或A的左子树包含B,或A的右子树包含Breturn isNodeSub(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);}private boolean isNodeSub(TreeNode node, TreeNode B) {// 1 如果B为空,说明B节点比对完成,匹配成功【终止条件】if (B == null ) {return true;}// 2 如果B不为null,且node为空,说明尚未匹配完B但已越过A的节点树叶子节点,匹配失败【终止条件】if (node == null ) {return false;}// 3 如果node节点值不等于B,则说明不是子结构,匹配失败【本层任务】if (node.val != B.val) {return false;}// 4 比较node与B的左右子节点,必须都满足条件才可以【返回值】return isNodeSub(node.left, B.left) && isNodeSub(node.right, B.right);}
}
复杂度分析
- 时间复杂度 O(MN): 其中 M,N分别为树 A 和 树 B 的节点数量;先序遍历树 A 占用 O(M) ,每次调用
recur(A, B)判断占用 O(N)。 - 空间复杂度 O(M) : 当树 A 和树 B 都退化为链表时,递归调用的深度取决于二叉树A的高度,最坏情况下,二叉树A是一个完全不平衡的树,高度为M,因此递归调用的最大深度为M。每次递归调用都需要一些额外的栈空间来保存函数调用的上下文,因此空间复杂度为O(M)