激活函数是什么?
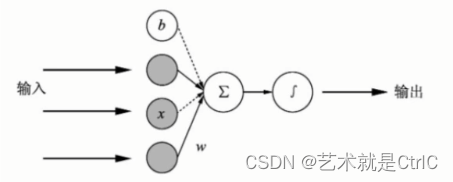
单个神经元的网络模型:
用计算公式表达如下:
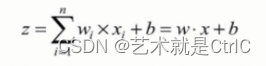
即在神经元中,输入的x通过与权重w相乘,与偏置量b求和后,还被作用了一个函数,这个函数就是激活函数。
激活函数的作用
如果没有激活函数,整个神经元模型就是一个简单的线性方程。而在现实生活中,线性方程能解决的事情相对比较简单,不能解决很多复杂的问题。比如使用神经网络模型模拟类似图像、视频、音频、语音这样的复杂数据,隐藏层之间存在非线性特点,需要使用激活函数来帮助模型理解并模拟这类数据。
激活函数对于人工神经网络模型学习、理解非常复杂的非线性函数来说具有十分重要的作用。通过它,可以将非线性因素引入到网络模型中,将模型中一个节点的输入信号转换成一个输出信号,该输出信号被用作下一层的输入,从而解决线性模型表达能力不足的缺陷。
示意图如下:
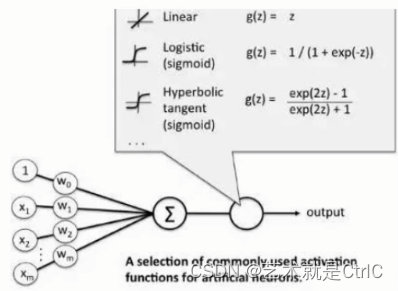
通过前面各输入值x和权重w的求和计算后输出结果,将输出结果作为激活函数的输入,从而增加模型解决负责问题的能力。
激活函数种类
激活函数有多种,早期研究神经网络主要采用sigmoid函数或者tanh函数,输出有界,很容易充当下一层的输入。近些年Relu函数及其改进型(如Leaky-ReLU、P-ReLU、R-ReLU等)在多层神经网络中应用比较多。
Sigmoid函数
Sigmoid函数,也叫Logistic函数,用于隐层神经元输出,该函数的数学公式、函数曲线和导数曲线如下:
计算公式: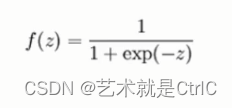
函数、导数曲线: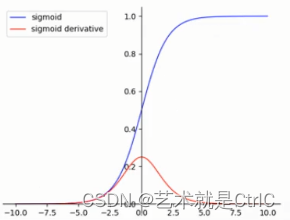
可以看到:Sigmoid函数连续、光滑、严格单调,是一个非常良好的阈值函数。x可以是正无穷到负无穷,但是对应的y却只有0~1的范围,所以,经过Sigmoid函数输出的函数都会落在0~1的区间里,即Sigmoid函数能够把输入的值"压缩"到0~1之间。
随着x趋近正负无穷大,y对应的值越来越接近1或-1的情况叫做饱和。处于饱和态的激活函数意味着,当x=100和x=1000时的反映都是一样的,这样的特性转换相当于将1000大于100十倍这个信息给丢失了。为了能有效使用Sigmoid函数,x的极限也只能是-6~6之间,而在-3~3之间时应该会有比较好的效果。由于Sigmoid函数的值域范围限制在(0,1)之间,这和概率值的范围[0,1]很接近,所以二分类的概率常常用这个函数。
优点 : ①平滑②易于求导
缺点 : ①在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失,其中梯度爆炸发生的概率非常小,而梯度消失发生的概率比较大
②Sigmoid的output不是0均值,即不以(0,0)为中心点。这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入,会产生一个结果,即当x>0,f=(w^T)x+b时,对w求局部梯度则都为正,这样在反向传播的过程中w要么都往正方向更新,要么都往负方向更新,从而产生捆绑的现象,使得收敛速度比较缓慢
③其解析式中含有幂运算,计算机求解时相对来讲比较耗时。对于规模比较大的深度网络,这会较大地增加训练时间。
在TensorFlow中对应的函数为:tf.nn.sigmoid(x,name = None),其中nn代表TensorFlow用于深度学习计算的核心模块。
模拟Sigmoid函数示例代码如下:
import matplotlib.pyplot as plt
import numpy as npdef sigmoid(x):return 1./(1. + np.exp(-x))def plot_sigmoid():x = np.arange(-6,6,0.2)y = sigmoid(x)plt.plot(x,y)plt.show()if __name__ == "__main__":plot_sigmoid()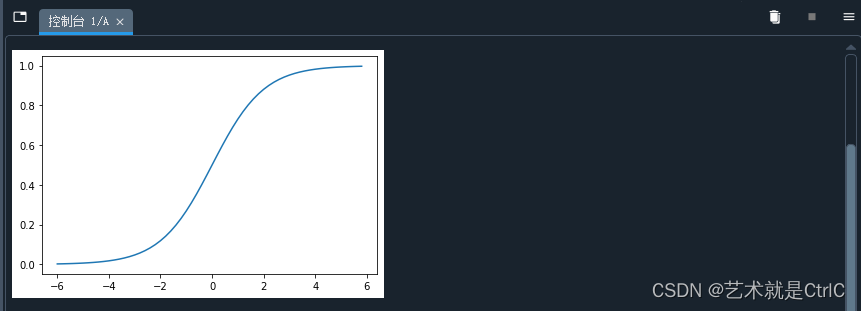
Tanh函数
Tanh函数,也叫双曲正切函数。该函数在Sigmoid函数值域范围(0~1)的基础上,将值域范围升级到了-1~1,可以说是Sigmoid函数的值域升级版。
计算公式:
函数、导数曲线: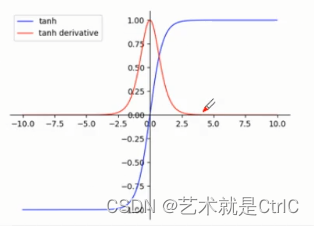
可以看到,x取值也是从正无穷到负无穷,但对应的y值变为-1~1之间,相对于Sigmoid函数有了更广的值域。Tanh函数在特征相差明显时的效果会很好,在循环过程中会不断扩大特征效果。但是,Tanh函数跟Sigmoid函数有一样的缺陷,即饱和问题,所以在使用Tanh函数时,要注意输入值的绝对值不能过大,否则模型无法训练。
优点 : ①Tanh函数的导数比Sigmoid函数的导数数值更大,即梯度变化更快,在训练过程中收敛速度更快
②输出范围为-1到1之间,可以使得输出均值为0,即以(0,0)为中心点,这个性质可以提高BP训练的效率
③可以将线性函数转变为非线性函数
缺点 : ①也存在梯度消失的情况,并没有解决Sigmoid梯度消失的问题
②幂运算依然比较耗时
在TensorFlow中对应的函数为:tf.nn.tanh(x,name = None)
模拟Tanh函数示例代码如下:
import matplotlib.pyplot as plt
import numpy as npdef tanh(x):return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))tanh_inputs = np.arange(-10,10,0.1)
tanh_outputs = tanh(tanh_inputs)plt.plot(tanh_inputs,tanh_outputs)
plt.xlabel("Tanh Inputs")
plt.ylabel("Tanh Outputs")
plt.show()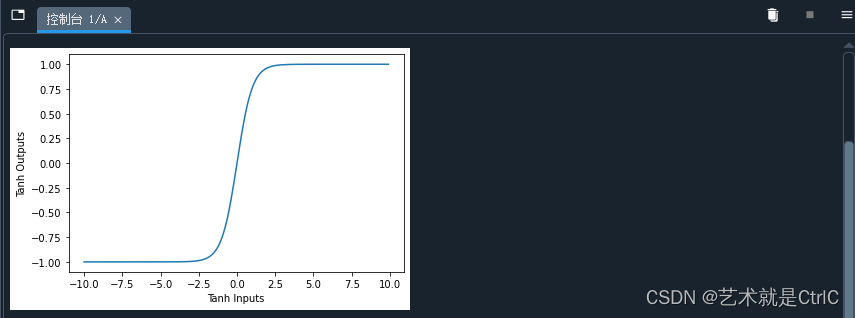
ReLU函数
ReLU函数,即线性整流函数,又称修正线性单元。
计算公式:
函数曲线: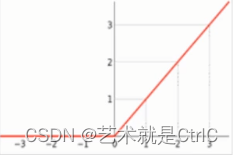
可以看到,ReLU函数对正向信号非常重视,忽略了负向信号。与人类神经元细胞对信号的反映很是类似。因此在神经网络中可以取得很好的拟合效果,应用十分广泛。
优点 : ①收敛速度比Sigmoid函数和Tanh函数快,解决了梯度爆炸、梯度消失的问题
②计算复杂度低,大大地提升了机器的运行效率
③适合用于后向传播
缺点 : ①ReLU的输出不是以(0,0)为中心点
②改动了输入数据的分布,下一层输入数据的分布跟前一层输入数据的分布不同,大大降低了模型的训练速度
③ReLU不会对数据做幅度压缩,数据的幅度会随着模型层数的增加不断扩张
④容易出现神经元死亡的问题,当输入接近零或为负时,函数的梯度变为零,网络将无法执行反向传播,也无法学习
在TensorFlow中,关于ReLU函数的实现,有以下两个对应的函数
tf.nn.relu(features,name = None),它是一般的ReLU函数,即max(features,0)
tf.nn.relu6(features,name = None),它是以6为阈值的ReLU函数,即min(max(features,0),6)
注意 : relu6存在的原因是防止梯度爆炸,当节点和层数特别多而且输出都为正时,它们相加后的和会是一个很大的值,尤其在经历几层变换之后,最终的值可能会离目标值相差太远,误差太大,会导致对参数调整修正值过大,从而引起网络抖动得较厉害,最终很难收敛。
Softplus函数
Softplus函数与ReLU函数十分类似,具体的函数曲线为下图中的蓝色虚线:
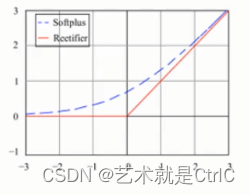
Softplus函数与ReLU函数的区别在于 : Softplus函数更加平滑,但是计算量很大,而且对于小于0的值保留的相对更多一点。
Softplus函数的计算公式:
在TensorFlow中,对应的函数为:tf.nn.softplus(features,name = None)
基于ReLU基础上的变种函数
从ReLU函数的曲线上知道,它在正向传播方面对信号的响应有很多优势,但忽略了负向信号,全部舍去了负值,很容易使模型输出全零导致无法再进行训练。例如,随机初始化的w中有个值是负值,相乘之后为负值,尽管对应的输入是正值,但输入值特征也会被全部屏蔽。同理,对应负值输入值反而被激活了。这显然不是我们想要的结果。于是在基于ReLU的基础上又演化出了一些变种函数。
Noisy relus函数 : 它为max中的x加了一个高斯分布的噪声,数学公式如下:

Leaky relus函数 : 它在ReLU基础上,保留一部分负值,让x为负时乘0.01,即Leaky relus对负信号不是一味地拒绝,而是缩小。其数学公式如下:
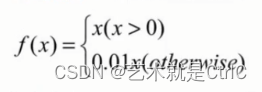
可以进一步让这个0.01作为参数可调,于是,当x小于0时,乘以a,a小于等于1。数学公式变为:
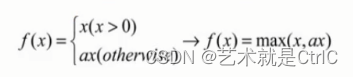
可以得到Leaky relus的公式为max(x,ax)
Leaky relus的函数曲线: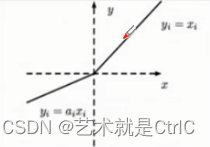
在TensorFlow中,Leaky relus公式没有专门的函数,可以利用现有函数组成而得到:tf.maximum(x,leak * x,name = name),其中leak为传入的参数,可以设为0.01等。
Elus函数 : Elus函数与ReLU函数一样都是不带参数的,而且收敛速度比ReLU函数更快,使用Elus函数时,不使用批处理比使用批处理能够获得更好的效果,同时Elus函数不使用批处理的效果比ReLU函数加批处理的效果要好。
数学公式: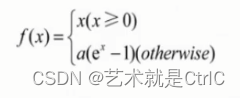
在TensorFlow中,Elus函数对应的函数为:tf.nn.elu(features,name = None)
Swish函数 : 谷歌公司发现的一个效果更优于Relu的激活函数。经过测试,在保持所有的模型参数不变的情况下,只是把原来模型中的ReLU激活函数修改为Swish激活函数,模型的准确率具有提升。
数学公式:
其中β为x的缩放参数,一般情况下取默认值1即可,在使用BN算法的情况下,还需要对x的缩放值β进行调整。β是个常数或可训练的参数。Swish具备无上界有下界、平滑、非单调的特性。Swish在深层模型上的效果优于ReLU。
在TensorFlow低版本中没有单独的Swish函数,可以手动封装,代码如下:
def swish(x,beta = 1):return x*tf.nn.sigmoid(x*beta)当beta去不同的值时,函数图像如下:
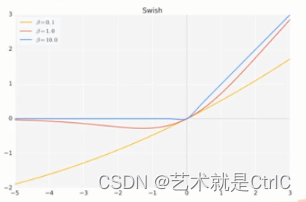
当β = 0时,Swish激活函数变为线性函数f(x) = x/2
当β = ∞时,Swish激活函数变为0或x,相当于ReLU
所以,Swish函数可以看作是介于线性函数与ReLU函数之间的平滑函数
激活函数总结
①神经网络中,运算特征是不断进行循环计算的,每个神经元的值也是在不断变化中。当特征相差明显时,Tanh函数的效果会很好,在循环过程中会不断扩大特征效果并显示出来。
②当计算的特征间相差虽较复杂却没有明显的区别,或者特征间的相差不是特别大时,需要更细微的分类判断,这时sigmoid函数的效果会好一些。
③ReLU函数的优势在于,其处理后的数据具备更好的稀疏性,即:将数据转化为只有最大数值.其他都为0,这种变换可以近似程度地最大保留数据特征,用大多数元素为0的稀疏矩阵来实现。以稀疏性数据来表达原有数据特征的方法,使得神经网络在迭代运算中能够取得又快又好的效果,因此目前大多数用max(0,x)来代替Sigmoid函数。