目录
一、针孔摄像机和透镜
1. 针孔摄像机的原理
2. 近轴折射模型
3. 镜头畸变问题
二、摄像机几何
1. 数学基础
2. 相机坐标系(空间点)→像素坐标系的映射关系:
3. 规范化投影变换
4. 投影变换的性质
三、其他摄像机模型
1. 弱透视投影摄像机
2. 正交投影摄像机
3. 透视投影摄像机和正交投影摄像机的比较
4. 各种摄像机模型的应用场合
一、针孔摄像机和透镜
1. 针孔摄像机的原理
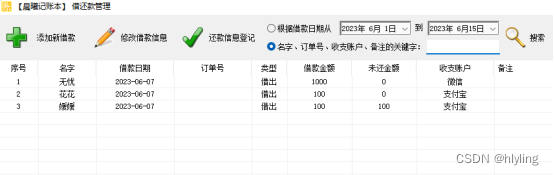
如果将胶片直接放置在物体前方,物体的每一个点都会发散出很多束光线,胶片上的每一个点都会叠加物体不同位置发出的光线,这样没有办法在胶片上清晰地成像。
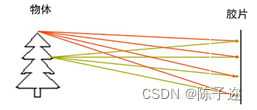
如果在物体和胶片中间加一块隔板,隔板中间有一个小针孔,这样隔板会滤除大部分对成像产生干扰的光束,最后在胶片上呈现出一个倒立的像。这就是“小孔成像”原理的直观解释。 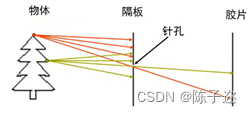
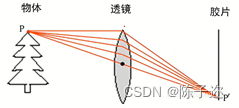
针孔摄像机就利用了“小孔成像”原理,示意图如下:
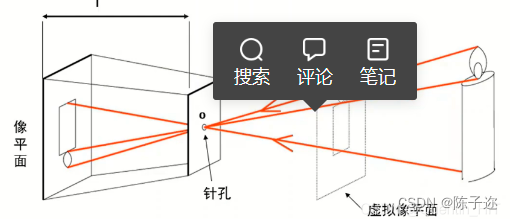
其中,f=焦距,o=光圈=针孔=摄像机中心。虚拟相平面与真实像平面对称,内容一样,x, y方向与真实相平面相反。实际处理中默认分析的是虚拟像平面。
随着光圈减小,成像效果越来越清晰,但是图像越来越暗。为了解决这一问题,可以增加透镜,将多条光线聚焦到胶片上,增加照片的亮度。
2. 近轴折射模型
在凸透镜成像中,我们只关心透镜和胶片之间的距离,其中。

由上图可以看出,凸透镜成像与小孔成像满足同样的相似关系。因此,凸透镜成像满足以下关系:
3. 镜头畸变问题
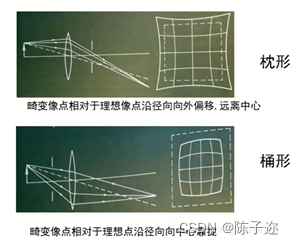
由于镜头制造工艺不完美,镜头形状存在缺陷,因此相机成像会发生畸变。畸变主要分为径向畸变和切向畸变,这里主要考虑径向畸变。
径向畸变可以分为枕形畸变和桶形畸变。通常情况下,广角镜头容易产生桶形畸变,而长焦镜头则更容易出现枕形畸变。
二、摄像机几何
1. 数学基础
图像点(欧式坐标→齐次坐标):
空间点(欧式坐标→齐次坐标):
图像点(齐次坐标→欧式坐标):
空间点(齐次坐标→欧式坐标):
注意:如果两个齐次坐标成比例,如,则和对应的欧式坐标是相等的。
2. 相机坐标系(空间点)→像素坐标系的映射关系:
其中,和单位:像素/米。通常令,单位:像素。
注意:
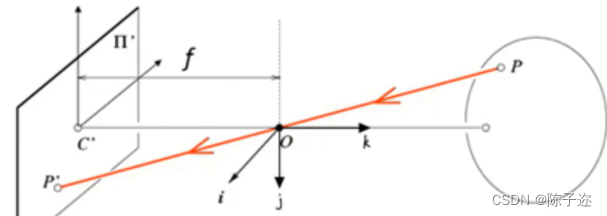
实际标定中,相机坐系,轴的方向是与像素坐标系,轴的方向(注意:此处成像平面为虚拟像平面)相同的,而像素坐标系,轴的方向是人为规定的,一般是左上角第一个像素为坐标原点,向右为轴正方向,向下为轴正方向。
实际处理时都是使用虚拟像平面。虚拟像平面与像平面坐标系相比,, 轴反向。
在上图中,假设相机与物体之间存在一个虚拟像平面,则像素坐标原点一般为从左向右观察到的虚拟相平面的左上角。
设为像素点的齐次坐标,为像素点的欧式坐标,为空间点相对于相机坐标系的齐次坐标,可以写出:
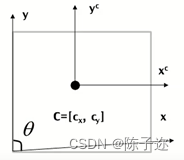
当摄像机不存在偏斜时,摄像机的投影矩阵如上。但是实际中摄像机可能偏斜,如下图所示:
3. 规范化投影变换
规范化投影变换(Normalization Projection Transform)是一种图像处理技术,用于将图像从原始的任意尺寸和形状变换为标准化的尺寸和形状。
规范化投影变换通常包括以下步骤:
-
提取关键点:根据特定任务需求,在原始图像中选择一些关键点,例如人脸识别中的眼睛、嘴巴等特征点。
-
计算变换矩阵:根据选定的关键点,利用几何变换方法(如仿射变换或透视变换),计算出一个变换矩阵。这个矩阵描述了如何将原始图像中的关键点映射到目标标准化尺寸和形状的位置。
-
应用变换:使用计算得到的变换矩阵,对原始图像进行变换。通过应用变换,原始图像中的关键点将被重新定位到标准化图像中的相应位置,从而实现图像的规范化。
4. 投影变换的性质
- 点投影为点
- 线投影为线
- 近大远小
- 角度不再保持
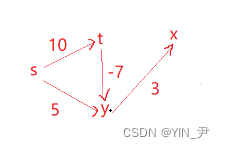
- 平行线相交(3D世界中的平行线在图像中相交于“影消点”)
三、其他摄像机模型
1. 弱透视投影摄像机
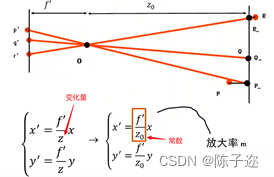
注意:
弱透视投影摄像机的透视投影矩阵的最后一行一定是0 0 0 1。
2. 正交投影摄像机
当摄像机中心到像平面的距离无限远时,空间点和像平面点的坐标呈1:1的比例关系。
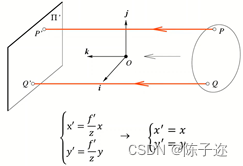
3. 透视投影摄像机和正交投影摄像机的比较

4. 各种摄像机模型的应用场合
- 正交投影:更多应用在建筑设计(AutoCAD)或者工业设计行业。
- 弱透视投影:在数学方面更简单。当物体较小且较远时准确,常用于图像识别任务。
- 透视投影:对于3D到2D映射的建模更为准确。用于运动恢复结构或SLAM。