目录
一、最大流有关的概念
例1
1、容量网络的定义
2、符号设置
3、建立模型
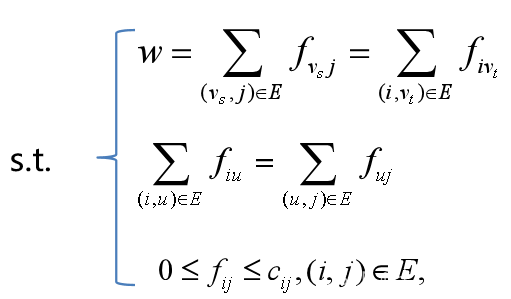
3.1 每条边的容量限制
3.2 平衡条件
3.3 网络的总流量
4、网络最大流数学模型
5、计算
二、最小费用流
例2
【符号说明】
【建立模型】
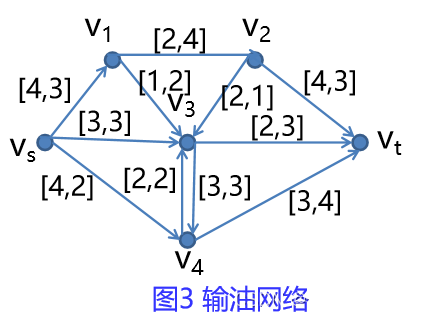
(1)各条边的流量限制
(2)网络总流量
(3)网络总费用
(4)中间点的流量平衡
【数学模型】
【模型求解】
三、最大匹配问题
例3
【问题假设】
【问题分析】
【符号设置】
【数学模型】
【模型求解】
一、最大流有关的概念
最大流是应用广泛的一类问题,例如交通运输网络中的人流、车流、物流;供水网络中的水流、金融系统中的资金流;通讯系统中的信息流。上世纪50年代Ford,Fulkerson建立的《网络流理论》是网络应用的基础。
例1
如图1所示网络为输油管道网络,vs为起点,vt为终点,v1,v2,v3,v4为中转站,边上的数字表示该管道的最大输油能力(t/h)。问如何安排各管道的输油量,才能使得从vs到vt的输油量最大。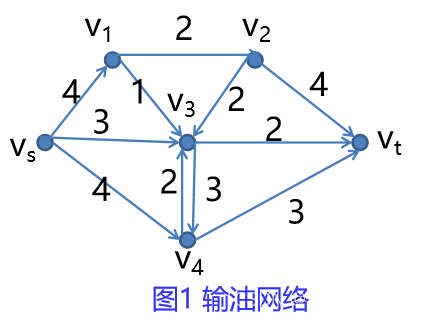
1、容量网络的定义
设有连通图G=(V,E),G的每一条边(vi,vj)上有非负数cij称为容量,仅有一个入次为0的点vs称为发点(源),一个出次为0的点vt称为收点(汇),其余点位中间点,这样的网络G称为容量网络,记为G=(V,E,C)。如图1所示。
2、符号设置
- Cij 边(i,j)的容量限制;
- fij 边(i,j)的实际流量;(称f={fij}为网络的一个流。)
- W 网络的总流量;
3、建立模型
3.1 每条边的容量限制
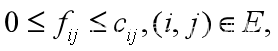
3.2 平衡条件
对中间点u,流入=流出,即
3.3 网络的总流量
称发点流量之和或汇点流量之和为网络总流量(忽略损失)。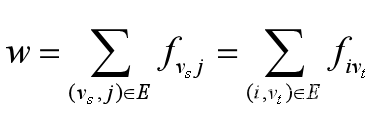
4、网络最大流数学模型
![]()
5、计算
编写例1的Lingo计算程序,将计算结果填入表1,将数据反映如图1,得到图2.
sets:
dian/vs v1 v2 v3 v4 vt/:;
bian(dian,dian)/vs,v1 vs,v3 vs,v4 v1,v2 v1,v3 v2,v3 v2,vt v3,vt v3,v4 v4,v3 v4,vt/:c,f;
endsets
data:
c=4 3 4 2 1 2 4 2 3 2 3;
enddata
max=w;
w=@sum(bian(i,j)|j#eq#6:f(i,j));
@for(bian(i,j):f(i,j)<c(i,j));
@for(dian(k)|k#ne#1#and#k#ne#6:@sum(bian(i,k):f(i,k))=@sum(bian(k,j):f(k,j)));表1 流量分布(不唯一)
| fij | V1 | V2 | V3 | v4 | vt |
| Vs | 3 | 4 | |||
| V1 | 2 | 1 | |||
| V2 | 2 | ||||
| V3 | 1 | 2 | |||
| v4 | 2 | 3 |
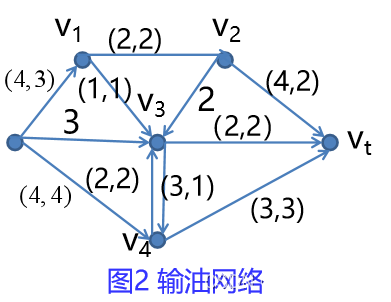
如图2所示,称形如(vs,v4),(v4,vt),(v4,v3),(v1,v2),(v1,v3)为饱和边;其余的边都是非饱和边。
要增大网络的流量,必须对饱和边扩容!!
二、最小费用流
设G=(V,E,C)为流量网络,边(i,j)除了容量限制cij外,还有因为流量而产生的单位费用dij(dij>0),记为G=(V,E,C,d)。这时如果不管流量大小,而只把网络流产生的费用当产目标,最优解必定是0,即各条边的实际流量为0时费用最小。研究方法必须改变为保持流量一定的情况下,使得流量产生的总费用最小。当网络流量保持最大而流量费用最小的网络流称为最小费用最大流。
例2
如图3所示网络G=(V,E,c,d),每条边有两个数字,第一个是容量限制,第二个是流量产生的单位费用。求该网络的最小费用最大流(最大流例1求得为7)。
【符号说明】
- G=(V,E,c,d] 如图3所示网络图;
- Cij 边(i,j)的管道容量限制;
- Dij 边(i,j)的单位费用;
- Xij 边(i,j)的实际流量;
- W 网络G的总流量。
【建立模型】
(1)各条边的流量限制
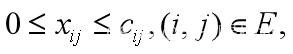
(2)网络总流量
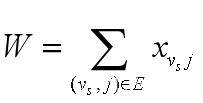
(3)网络总费用
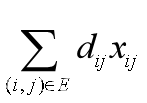
(4)中间点的流量平衡

【数学模型】
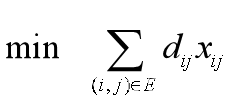
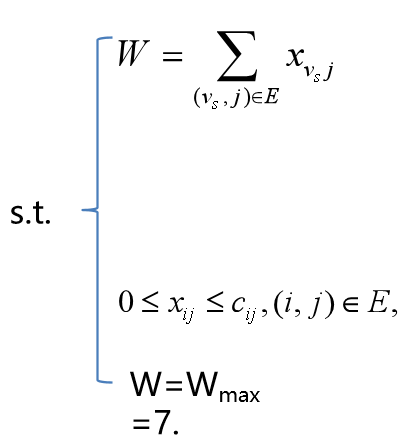
【模型求解】
编写lingo求解程序,计算得个各条边的实际流量见表2和总费用为50.(总流量为7时)
sets:
dian/vs v1 v2 v3 v4 vt/:;
bian(dian,dian)/vs,v1 vs,v3 vs,v4 v1,v2 v1,v3 v2,v3 v2,vt v3,vt v3,v4 v4,v3 v4,vt/:c,x,d;
endsets
data:
c=4 3 4 2 1 2 4 2 3 2 3;
d=3 3 2 4 2 1 3 3 3 2 4;
enddata
min=@sum(bian:d*x);
w=@sum(bian(i,j)|j#eq#6:x(i,j));
@for(bian(i,j):x(i,j)<c(i,j));
@for(dian(k)|k#ne#1#and#k#ne#6:@sum(bian(i,k):x(i,k))=@sum(bian(k,j):x(k,j)));
w=7;
表2 最小费用的流量分布
| fij | V1 | V2 | V3 | v4 | vt |
| Vs | 2 | 2 | 3 | ||
| V1 | 2 | ||||
| V2 | 2 | ||||
| V3 | 2 | ||||
| v4 | 3 |
三、最大匹配问题
问题来源:
有n个人,m件工作,每个人的工作能力不同,各能胜任某几项工作。假设每个只做一件工作;一件工作只需一个人做,怎样分配才能使得尽量多的工人有工作。
转化为匹配问题:
- x1,x2,…,xn表示工人;
- y1,y2,…,ym表示工作,
- X表示{x1,x2,…,xn}, Y表示{y1,y2,…,ym}。
这样就产生一个二部图G=(X,Y,E),其中E中的边(xi,yj)就表示xi胜任工作yj。如图4所示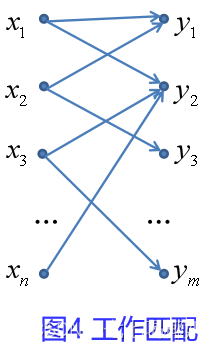
匹配定义:
二部图G=(X,Y,E),M是E的子集,M中任意两条边都没有公共端点,则称M是G的一个匹配(对集)。使得|M|达到最大的匹配称为最大匹配。
例3
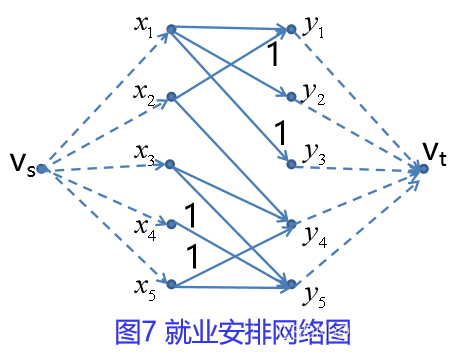
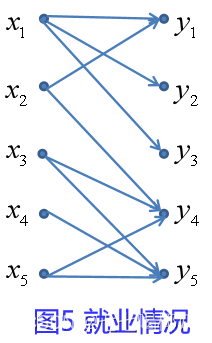
设有5位待业者,5项工作,他们各自能胜任的工作情况如图5所示,设计一个就业方案,使尽量多人能就业。
【问题假设】
一人最多一工作,一工作最多一人。
【问题分析】
注意到,对xi来说,出次可能不唯一,但最多有一条边可能实现;对yj来说,入次可能不唯一,但也最多一条边实现。根据流量平衡,在xi前置vs作为发点;在yj后置vt作为汇点,将图5改造为流量网络,见图六。
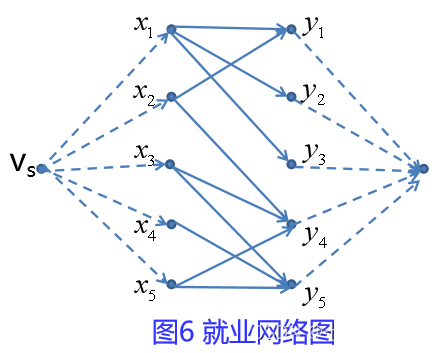
如图6所示流量网络图G=(V,E,C),其中每条边的容量都为1.
【符号设置】
- G=(V,E,C)流量网络图,如图6;
- vs 发点;
- vt 汇点;
- x1,…,x5,y1,…,y5,网络中间点;
- Cij 边(i,j)的容量限制,且cij=1,(i,j)∈E;
- xij 边(i,j)的实际流量,且只取0-1;
【数学模型】
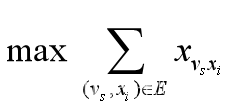
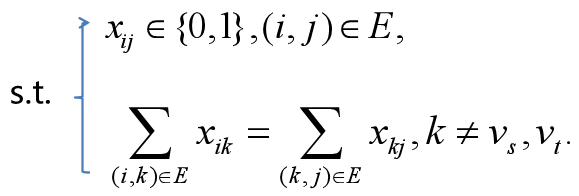
【模型求解】
编写Lingo程序,计算得到最大匹配为4,具体安排反映在图6上,见图7.
sets:
dian/vs x1 x2 x3 x4 x5 y1 y2 y3 y4 y5 vt/:;
bian(dian,dian)/vs,x1 vs,x2 vs,x3 vs,x4 vs,x5
x1,y1 x1,y2 x1,y3 x2,y1 x2,y4 x3,y4 x3,y5 x4,y5
x5,y4 x5,y5 y1,vt y2,vt y3,vt y4,vt y5,vt/:x,c;
endsets
data:
c=1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1;
enddata
n=@size(dian);
max=@sum(bian(i,j)|i#eq#1:x(i,j));
@for(bian:@bin(x));
@for(bian:x<c);
@for(dian(k)|k#ne#1#and#k#ne#n:@sum(bian(i,k):x(i,k))=@sum(bian(k,j):x(k,j)));