目录
一:十进制转换为二进制、八进制、十六进制
(1)整数转换
(2)小数转换
1)十进制转二进制
2)十进制转八进制
3)十进制转十六进制
二:二进制、八进制、十六进制转换为十进制
三:二进制转八进制,十六进制
1)二进制数1010 0100B转换成八进制数为244Q
2)二进制数1010 0100B转换成十六进制数为:a4H
3)二进制转八进制,八进制转二进制
4)二进制转十六进制,十六进制转二进制
四:八进制与十六进制之间的转换
五:工具
整型有4种进制形式:
- 二进制是由数字0-1组成,逢二进一,结尾用B表示,例如10B
- 八进制是由数字0-7组成,逢八进一,结尾用Q表示,例如76Q
- 十进制是由数字0-9组成,逢十进一,开头不能是0,结尾用D表示,例如16D
- 十六进制是由数字0-9和字母A-F组成,为了和其他进行区别通常开头是0X,开头不能是0,结尾用H表示,例如9336H
一:十进制转换为二进制、八进制、十六进制
(1)整数转换
十转二原理:除以2,反向取余数,直到商为0,将所有的余数最终逆序输出
例如:9(十进制)→1001(二进制)
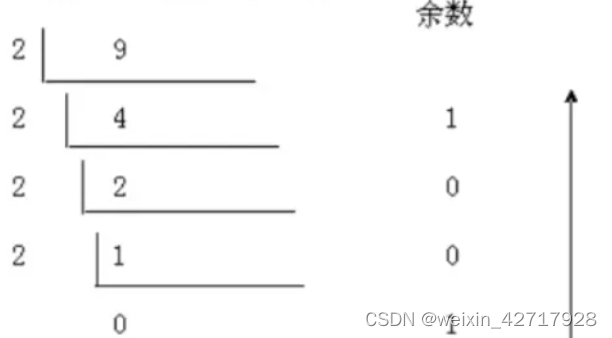
十转八,或者十六机制同理,需要注意的是,十六进制数是由0-9和A-F(或者a-f)组成的,A相当于十进制中的10,B相当于11,依次类推,F相当与15,下述中取得的余数12即为十六进制中的c

(2)小数转换
1)十进制转二进制
原理:十进制小数转换成二进制小数采用 “乘2取整,顺序输出” 法
例如:十进制小数0.68转换为二进制数
具体步骤:
0.68* 2=1.36 -->1
0.36* 2=0.72 -->0
0.72* 2=1.44 -->1
0.44* 2=0.88–>0
0.88* 2=1.76 -->1
0.68D–>0.10101B(精确到小数点后5位)
PS这里的D和B表达的意思是十进制,二进制
2)十进制转八进制
原理:思路跟上面一样
十进制数10.68转换成八进制数,分为整数部分和小数部分求解
步骤:
(1)整数部分
10/8=1 -->2
1/8=0 -->1
倒序输出为12
(2)小数部分
0.68* 8=5.44 -->5
0.44* 8=3.52 -->3
0.52* 8=4.16 -->4
已经达到了题目要求的精度,即可结束
则小数部分为:0.68–>0.534
因此10.68D -->12.534Q
3)十进制转十六进制
同理
(1)整数部分
25/16=1 -->9
1/16=0 -->1
倒序输出为:19
(2)小数部分
0.68* 16=10.88 -->a(即十进制中的10)
0.88* 16=14.08 -->e
0.08* 16=1.28 -->1
已经达到了要求的精度,顺序输出为:ae1
则:25.68D -->19.ae1H(精确到小数点后3位)
二:二进制、八进制、十六进制转换为十进制


三:二进制转八进制,十六进制
1)二进制数1010 0100B转换成八进制数为244Q

2)二进制数1010 0100B转换成十六进制数为:a4H

3)二进制转八进制,八进制转二进制

4)二进制转十六进制,十六进制转二进制

四:八进制与十六进制之间的转换
两者之间的转换可以借助十进制或者二进制完成,可以先将八进制转换成十进制或二进制,再转换成十六进制。通过间接转换来实现
五:工具
在线进制数转换/换算工具(2进制,3进制,4进制,8进制,10进制,16进制,24进制,32进制等进制转换)