吴恩达《机器学习》2-2-＞2-4:代价函数

一、代价函数的概念

代价函数是在监督学习中用于评估模型的性能和帮助选择最佳模型参数的重要工具。它表示了模型的预测输出与实际目标值之间的差距，即建模误差。代价函数的目标是找到使建模误差最小化的模型参数。

二、代价函数的理解

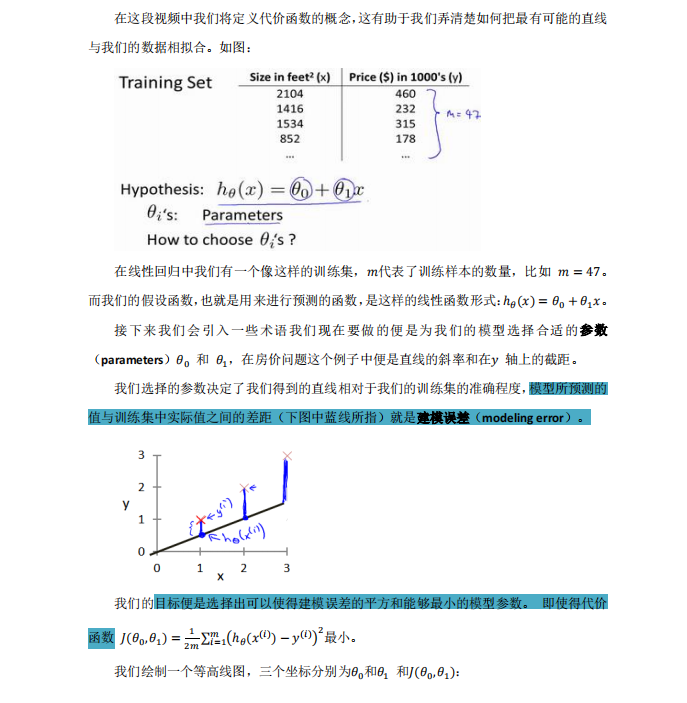
训练集数据：假设我们有一个训练集，其中包含 𝑚 个样本（数据点），每个样本都有一个特征 𝑥 和一个对应的目标值 𝑦。

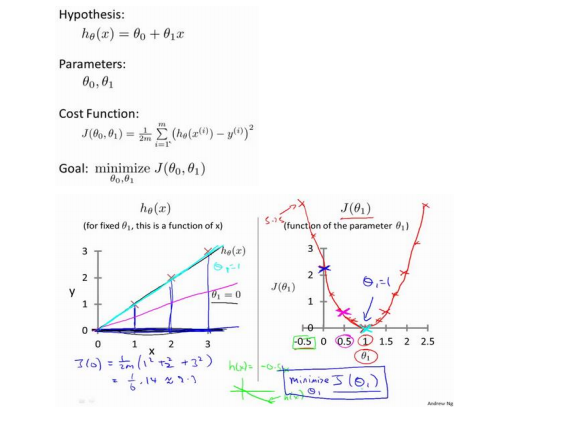
模型的假设函数：我们构建一个假设函数 ℎ𝜃(𝑥) 用于预测目标值 𝑦。在单变量线性回归中，这个假设函数是一条直线，可以用一对参数（𝜃0 和 𝜃1）来表示。模型的目标是通过调整这些参数来拟合训练数据，以便 ℎ𝜃(𝑥) 接近真实目标值 𝑦。

建模误差：模型的预测值 ℎ𝜃(𝑥) 与实际目标值 𝑦 之间存在差距，这个差距被称为建模误差（modeling error）。代价函数的目标是度量这些建模误差。

平方误差代价函数：在单变量线性回归问题中，我们使用平方误差代价函数来度量建模误差的大小。这个代价函数计算每个样本的建模误差（即预测值与实际值之间的差）的平方，并将所有样本的平方误差求和，然后取平均值。这使得代价函数具有如下形式：

𝐽(𝜃0, 𝜃1) = 1/2𝑚 ∑ (ℎ𝜃(𝑥(𝑖)) − 𝑦(𝑖))^2

其中，𝐽(𝜃0, 𝜃1) 代表代价函数，𝜃0 和 𝜃1 是模型参数，𝑚 是训练集中的样本数量，ℎ𝜃(𝑥(𝑖)) 是模型的预测值，𝑦(𝑖) 是实际的目标值。

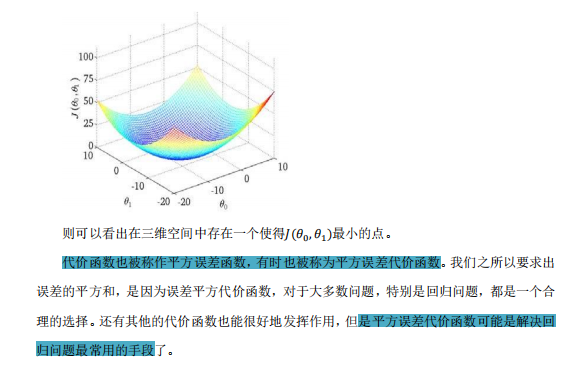
最小化代价函数：通过调整模型参数 𝜃0 和 𝜃1，我们的目标是最小化代价函数 𝐽(𝜃0, 𝜃1)。这意味着我们寻找那些能够使建模误差的平方和最小的模型参数，以使模型更好地拟合训练数据。