数据可视化PCA与t-SNE

PCA（主成分分析）和t-SNE（t分布随机近邻嵌入）都是降维技术，可以用于数据的可视化和特征提取。

降维：把数据或特征的维数降低，其基本作用包括：

提高样本密度，以及使基于欧氏距离的算法重新生效
数据预处理。对数据去冗余、降低信噪比
方便可视化

降维主要可以分为线性降维和非线性降维

线性降维
- 侧重让不相似的点在低维表示中分开
- MDS（Multiple Dimensional Scaling，多维缩放）
- PCA（Principle Components Analysis，主成分分析）
非线性降维
- 非线性降维中用到的方法大多属于流形学习方法
- 这类技术假设高维数据实际上处于一个比所处空间维度低的非线性流形上，因此侧重让相似的近邻点在低维表示中靠近
- Sammon mapping
- SNE（Stochastic Neighbor Embedding，随机近邻嵌入），t-SNE是基于SNE的
- Isomap（Isometric Mapping，等度量映射）
- MVU（Maximum Variance Unfolding）
- LLE（Locally Linear Embedding，局部线性嵌入）等

1.PCA

1.1. PCA的原理

主成分分析（Principal Component Analysis，PCA）是一种常用的数据降维方法，它通过将原始数据投影到一个新的坐标系中，将数据中的冗余信息消除，并保留最有用的信息。具体来说，PCA会找到数据中的主成分，将数据沿着主成分方向进行旋转，使得旋转后的数据方差最大。这样可以有效减少数据的维度，从而降低模型复杂度，避免过拟合。

假设我们有一个数据集X={x1,x2,...,xn}，其中 $x_i \in \mathbb{R}^d$ ，我们的目标是将数据从 d维降至 k维（k<d）。PCA 的基本思想是找到一个正交基，使得数据在这组基上的投影方差最大。具体来说，我们可以按照以下步骤进行 PCA：

对数据进行中心化处理，即对每个维度减去该维度上的均值，使得数据的均值为 0。
计算协方差矩阵 C，其中 $C_{i,j}$ 表示 x 在第 i 个维度和第 j个维度上的协方差。
对协方差矩阵进行特征值分解，得到特征值 $\lambda_1,\lambda_2,...,\lambda_d$ 和对应的特征向量 $v_1,v_2,...,v_d$
。其中，特征向量 $v_i$ 表示数据在第 i 个维度上的投影方向。
选择前 k 个特征值对应的特征向量 $v_1,v_2,...,v_k$ ，将原始数据投影到这组基上。

下面是 PCA 的数学公式：

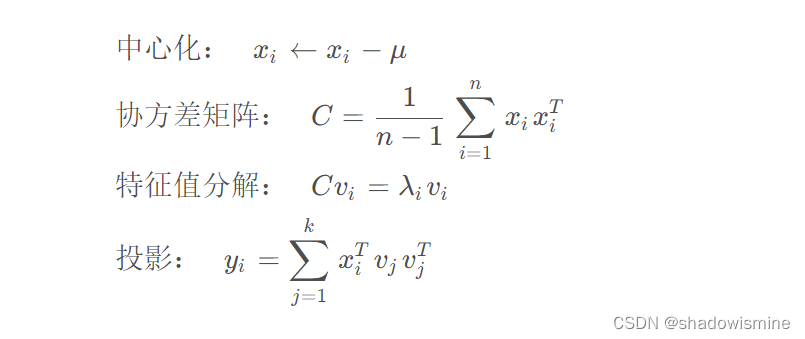
1.2. PCA的实现

在实现PCA算法时，我们需要执行以下步骤：

将数据集进行标准化，使得每个特征的均值为0，方差为1。这可以通过对每个特征减去其均值并除以其标准差来实现。
计算数据的协方差矩阵。
对协方差矩阵进行特征值分解。
选择前k个特征值对应的特征向量作为新的基向量。
将原始数据投影到新的低维空间中。

在Python中，我们可以使用NumPy和SciPy库来实现PCA算法。以下是一个简单的示例代码，演示如何使用Python和NumPy实现PCA算法：

import numpy as npdef pca(X, k):# 标准化数据X_std = (X - np.mean(X, axis=0)) / np.std(X, axis=0)# 计算协方差矩阵cov_mat = np.cov(X_std, rowvar=False)# 特征值分解eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)# 选择前k个特征值对应的特征向量eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i]) for i in range(len(eigen_vals))]eigen_pairs.sort(reverse=True, key=lambda k: k[0])w = np.hstack([eigen_pairs[i][1].reshape(-1, 1) for i in range(k)])# 将原始数据投影到新的低维空间中X_pca = X_std.dot(w)return X_pca

在上面的代码中，我们使用numpy.cov()函数计算数据的协方差矩阵，使用numpy.linalg.eig()函数进行特征值分解，然后选择前k个特征值对应的特征向量。最后，我们将原始数据投影到新的低维空间中。

1.3 数据可视化

PCA可以将高维数据映射到二维或三维空间中，从而实现数据的可视化。这种可视化方式通常被称为“主成分分析图”或“PCA图”。下面我们以手写数字数据集为例，演示如何利用PCA进行数据可视化。

首先加载手写数字数据集：

from sklearn.datasets import load_digitsdigits = load_digits()
X = digits.data
y = digits.target

然后我们对数据进行PCA降维：

from sklearn.decomposition import PCApca = PCA(n_components=2)
X_pca = pca.fit_transform(X)

最后，我们将数据可视化：

import matplotlib.pyplot as pltplt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, alpha=0.5)
plt.colorbar()
plt.show()

运行上述代码后，我们可以得到一个二维的PCA图，其中不同颜色的点代表不同的手写数字，如下图所示：

这个图显示了手写数字数据集的PCA可视化结果。在这个二维图中，我们可以看到不同的数字在不同的区域内形成了簇。例如，数字0、6和1在左上角的区域内形成了簇，数字3、8和9在右下角的区域内形成了簇，数字2和7分别位于两个簇的中间位置。

PCA除了可以做数据可视化，也可以对数据进行降维操作。如在图像处理领域，我们常常需要将高维的像素点转化为低维的向量，以便于更好地进行图像分类、压缩等操作。使用PCA对图像进行降维处理是一种常见的方法。以人脸识别为例，我们可以使用PCA对人脸图像进行降维处理，将每张人脸图像转化为一个低维向量，然后使用这些向量进行人脸识别。

除此之外，PCA还可以做数据压缩和去噪。

2. t-SNE

t-SNE（t-Distributed Stochastic Neighbor Embedding）是一种非线性降维算法，用于将高维数据映射到低维空间。与PCA不同，t-SNE旨在保留数据点之间的局部关系，并在低维空间中反映这种关系，而不是仅仅保留方差最大的维度。它的主要思想是在高维空间中计算数据点之间的相似度，然后在低维空间中将这些相似度转换为概率分布，从而最小化原始空间和低维空间之间的KL散度（Kullback-Leibler Divergence）。
具体来说，对于每个数据点i，t-SNE首先计算它与其他数据点j之间的相似度 $p_{ij}$ ，并利用高斯分布函数转换为概率分布 $p_{j|i}$ ，表示如果在低维空间中，点i选择点j作为邻居点的概率。在低维空间中，每个点k被表示为 $q_{k}$ 的概率分布，表示如果在高维空间中，点i选择点j作为邻居点的概率。t-SNE通过最小化 $p_{ij}$ 和 $q_{ij}$ 之间的KL散度来优化这些概率分布，从而将高维数据映射到低维空间。

Python中有多个库可以实现t-SNE算法

from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, perplexity=30.0, early_exaggeration=12.0, learning_rate=200.0)
X_tsne = tsne.fit_transform(X)

其中，n_components指定了降维后的维度数，perplexity是t-SNE算法中的一个超参数，用于控制每个点周围的邻居数量，early_exaggeration是控制t-SNE计算过程中的簇大小的参数，learning_rate是学习率，控制梯度下降的步长。

2.1 t-SNE的应用

t-SNE主要用于可视化高维数据，特别是当我们想要探索数据中的局部结构时。例如，在自然语言处理中，我们可以使用t-SNE来可视化单词嵌入，以了解单词之间的语义关系。在图像处理中，t-SNE可以用于可视化图像的特征向量，以探索图像之间的相似性。

2.1.1 图像处理

t-SNE也可以用于图像处理中的特征提取和图像聚类。在这种情况下，我们可以使用卷积神经网络（CNN）提取图像特征，并使用t-SNE对这些特征进行降维，然后进行聚类或可视化。

例如，我们可以使用一个预先训练好的CNN模型，如VGG或ResNet，对图像进行特征提取。然后，我们可以使用t-SNE将这些高维特征降到二维或三维，以便进行可视化或聚类。

以下是一个使用t-SNE可视化MNIST数据集的示例：

import numpy as np
from sklearn.manifold import TSNE
from sklearn.datasets import fetch_openml
import matplotlib.pyplot as plt# 获取MNIST数据集
mnist = fetch_openml('mnist_784')
X, y = mnist.data / 255.0, mnist.target# 使用预训练的卷积神经网络（CNN）提取特征
# ...# 使用t-SNE降维
tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X_features)# 可视化降维后的数据
plt.figure(figsize=(10, 10))
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y.astype(int), cmap='jet')
plt.axis('off')
plt.colorbar()
plt.show()

该代码使用MNIST数据集作为示例数据集。首先，我们通过fetch_openml函数获取MNIST数据集，并对像素值进行归一化。然后，我们使用预训练的CNN模型提取图像的特征。最后，我们使用t-SNE将这些特征降至二维，并将结果可视化。

2.1.2 自然语言处理

t-SNE 在自然语言处理中也有广泛的应用，特别是在词向量的可视化方面。在自然语言处理中，我们经常使用词向量来表示单词。词向量是将每个单词表示为一个向量，使得每个向量都能够捕捉到该单词的语义信息。词向量通常在高维空间中表示，其中每个维度对应于单词的某个特定特征。

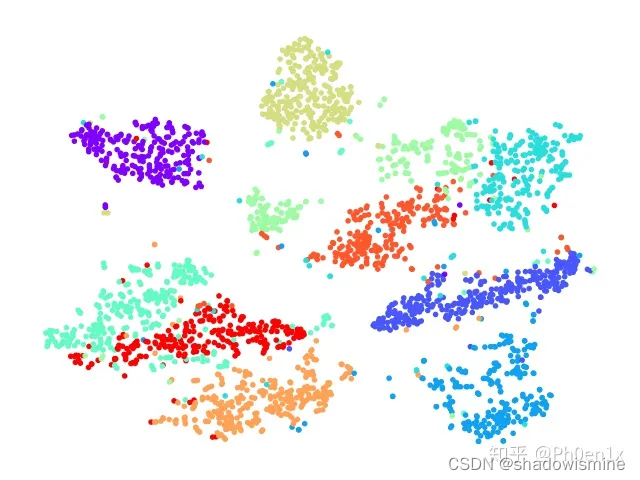
使用 t-SNE 可以将高维词向量降至 2 维或 3 维，然后使用二维或三维散点图将它们可视化。通过这种方式，我们可以更好地理解单词之间的相似性，例如，在这些可视化中，词向量非常相似的单词将在二维或三维空间中彼此靠近。

from sklearn.manifold import TSNE
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import CountVectorizer
import matplotlib.pyplot as plt# 加载新闻数据集
newsgroups = fetch_20newsgroups(subset='all',categories=['alt.atheism', 'comp.graphics','comp.os.ms-windows.misc', 'comp.sys.ibm.pc.hardware','comp.sys.mac.hardware', 'comp.windows.x', 'misc.forsale','rec.autos', 'rec.motorcycles', 'rec.sport.baseball','rec.sport.hockey', 'sci.crypt', 'sci.electronics','sci.med', 'sci.space', 'soc.religion.christian', 'talk.politics.guns','talk.politics.mideast', 'talk.politics.misc', 'talk.religion.misc'])# 抽取词频特征
vectorizer = CountVectorizer(stop_words='english')
X = vectorizer.fit_transform(newsgroups.data)# 使用t-SNE进行降维
tsne = TSNE(n_components=2, verbose=1, perplexity=40, n_iter=300)
X_tsne = tsne.fit_transform(X.toarray())# 将降维结果可视化
plt.scatter(X_tsne[:, 0], X_tsne[:, 1])
plt.show()

运行上述代码后，我们可以得到一个散点图，其中每个点代表一个单词，相似的单词会被放置在相似的位置，这有助于我们更好地理解单词之间的语义关系。

需要注意的是，对于大型数据集，t-SNE 可能需要很长时间才能完成降维。在这种情况下，可以尝试使用随机子采样来减少数据点数量。

3. 如何选择PCA还是t-SNE

在选择PCA或t-SNE时，需要考虑以下几个因素：

数据类型：如果数据是高维稠密的，那么PCA是一个更好的选择，因为t-SNE需要大量的计算资源来处理大规模数据。如果数据是低维或稀疏的，t-SNE是更好的选择。
目标：如果目标是可视化数据集并检查其聚类结构或在二维或三维空间中查看数据点的分布，t-SNE是更好的选择。如果目标是减少数据的维度以进行机器学习或其他应用，PCA是更好的选择。
计算资源：PCA是一个快速而直接的方法，而t-SNE需要更多的计算资源和时间。如果计算资源有限，PCA是更好的选择。

参考：https://blog.csdn.net/qq_33578950/article/details/130042918