CSDN每日一题学习训练——Java版（克隆图、最接近的三数之和、求公式的值）

版本说明

当前版本号[20231109]。

版本	修改说明
20231109	初版

克隆图

题目

给你无向连通(https://baike.baidu.com/item/连通图/6460995?fr=aladdin) 图中一个节点的引用，请你返回该图的深拷贝(https://baike.baidu.com/item/深拷贝/22785317?fr=aladdin)（克隆）。

图中的每个节点都包含它的值 val（int）和其邻居的列表（list[Node]）。

class Node {
public int val;
public List neighbors;
}

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将给定节点的拷贝作为对克隆图的引用返回。

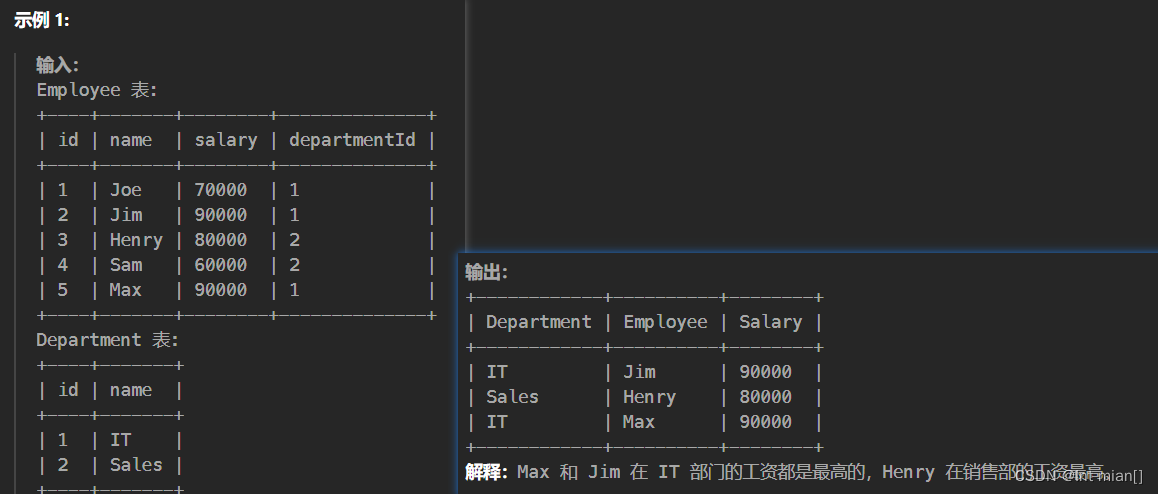
示例 1：

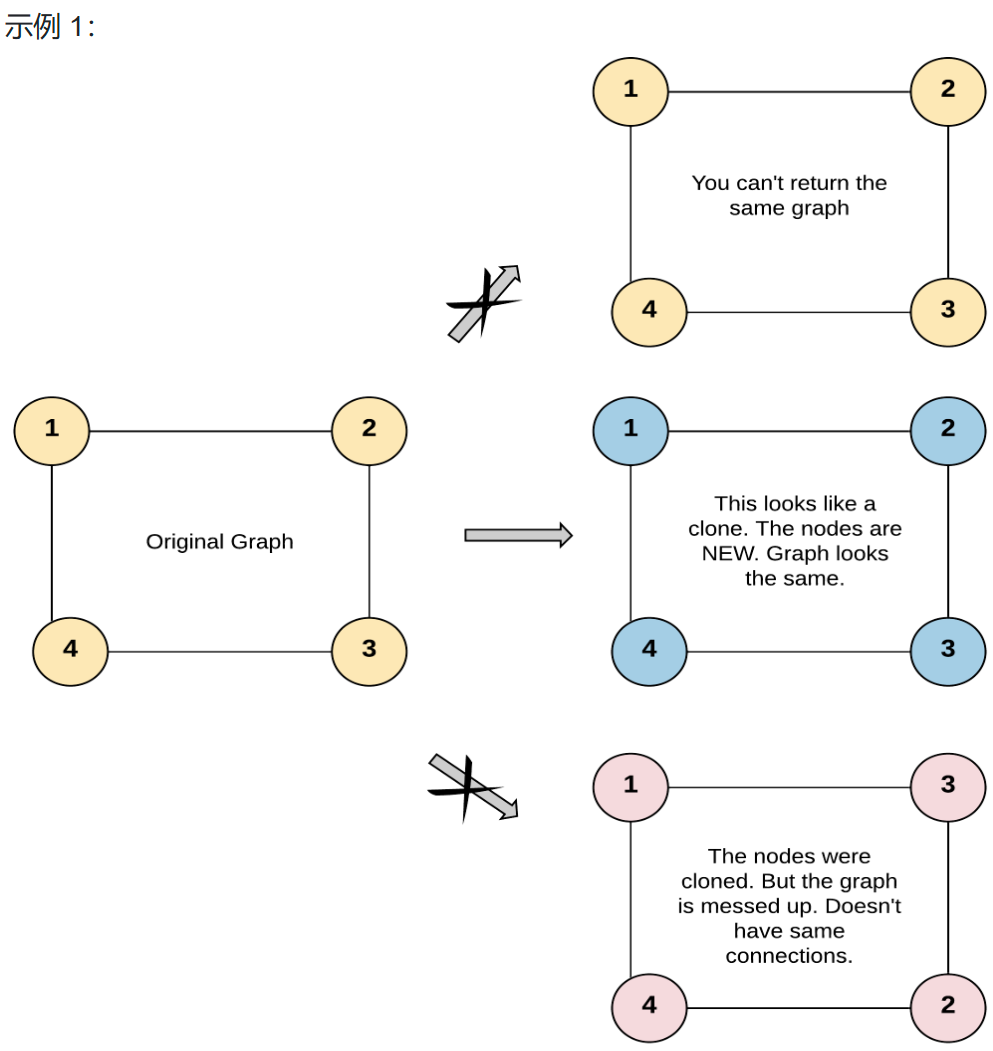
输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]

解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：

输入：adjList = [[]]
输出：[[]]

解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例 3：

输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。

示例 4：

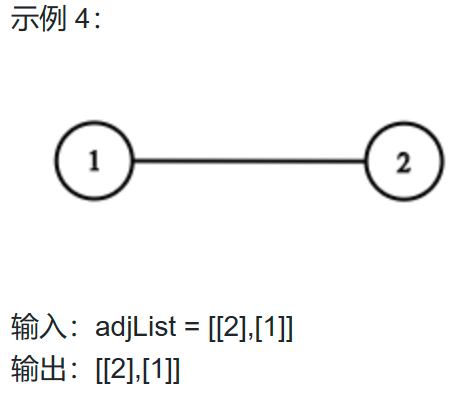
输入：adjList = [[2],[1]]
输出：[[2],[1]]

提示：

节点数不超过 100 。
每个节点值 Node.val 都是唯一的，1 <= Node.val <= 100。
无向图是一个简单图(https://baike.baidu.com/item/简单图/1680528?fr=aladdin)，这意味着图中没有重复的边，也没有自环。
由于图是无向的，如果节点 p 是节点 q 的邻居，那么节点 q 也必须是节点 p 的邻居。
图是连通图，你可以从给定节点访问到所有节点。

解题思路

创建一个哈希表，用于存储已访问过的节点及其对应的克隆节点。
使用深度优先搜索（DFS）遍历原图，对于每个节点： a. 如果该节点已经被访问过，则直接返回其克隆节点。 b. 创建一个新的克隆节点，并将其添加到哈希表中。 c. 遍历该节点的邻居列表，递归调用DFS函数，将邻居节点的克隆节点添加到克隆节点的邻居列表中。
返回克隆图的任意一个节点即可。

代码思路

首先定义了一个名为Node的类，表示图中的节点，包含一个整数值val和指向左右子节点的指针left和right，以及指向下一个节点的指针next。
```
class Node {public int val; // 节点的值public Node left; // 左子节点public Node right; // 右子节点public Node next; // 下一个节点
}
```
同时，还定义了一个名为Solution的类，其中包含了两个方法：cloneGraph和DFS。
cloneGraph方法是主要的入口点，它接受一个Node类型的参数node，表示要克隆的图的起始节点。
```
 // 克隆图的方法，接收一个节点作为参数public Node cloneGraph(Node node)
```
该方法首先创建一个空的哈希表visited，用于存储已经访问过的节点及其对应的克隆节点。然后调用DFS方法进行深度优先搜索，从起始节点开始遍历整个图，并返回克隆后的图的根节点。
```
  // 创建一个哈希表，用于存储已访问过的节点HashMap<Node, Node> visited = new HashMap<>();// 调用深度优先搜索方法进行克隆return DFS(node, visited);
```
DFS方法是一个递归方法，用于实现深度优先搜索。它接受两个参数：当前节点node和一个哈希表visited，用于记录已经访问过的节点及其对应的克隆节点。
```
  // 深度优先搜索方法，接收一个节点和一个哈希表作为参数public Node DFS(Node node, HashMap<Node, Node> visited) 
```

在方法内部，首先判断当前节点是否为空，如果为空则直接返回。接着判断当前节点是否已经被访问过，如果已经访问过则直接返回其对应的克隆节点。然后创建一个新的克隆节点clone，并将其添加到visited哈希表中。

 // 如果节点为空，返回空节点if (node == null) {return node;}// 如果哈希表中已经存在该节点的克隆，直接返回克隆节点if (visited.containsKey(node)) {return visited.get(node);}// 创建一个新的克隆节点，值为原节点的值，邻居列表为空Node clone = new Node(node.val, new ArrayList<>());// 将原节点和克隆节点添加到哈希表中visited.put(node, clone);

最后，遍历当前节点的所有邻居节点，对每个邻居节点递归调用DFS方法，并将返回的克隆节点添加到当前节点的克隆节点的邻居列表中。最终返回当前节点的克隆节点。

         // 遍历原节点的邻居节点，递归调用DFS方法进行克隆，并将克隆后的邻居节点添加到克隆节点的邻居列表中for (Node n : node.neighbors) {clone.neighbors.add(DFS(n, visited));}// 返回克隆节点return clone;

这段代码实现了一个简单的图的深度优先搜索和克隆过程，可以用于处理一些需要复制或克隆图结构的场景。

参考代码

class Node {public int val;public Node left;public Node right;public Node next;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, Node _left, Node _right, Node _next) {val = _val;left = _left;right = _right;next = _next;}
};
class Solution {public Node cloneGraph(Node node) {HashMap<Node, Node> visited = new HashMap<>();return DFS(node, visited);}public Node DFS(Node node, HashMap<Node, Node> visited) {if (node == null) {return node;}if (visited.containsKey(node)) {return visited.get(node);}Node clone = new Node(node.val, new ArrayList<>());visited.put(node, clone);for (Node n : node.neighbors) {clone.neighbors.add(DFS(n, visited));}return clone;}
}

最接近的三数之和

题目

给定一个包括 n 个整数的数组 nums 和一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。

示例：

输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。

提示：

3 <= nums.length <= 10^3
-10^3 <= nums[i] <= 10^3
-10^4 <= target <= 10^4

解题思路

首先对数组进行排序，这样可以方便后续的查找操作。
使用两层循环遍历数组中的每两个数的组合，计算它们的和，记为twoSum。
对于每个twoSum，我们需要找到一个与它最接近的数，使得这三个数的和与目标值target最接近。我们可以使用递归的方法来实现这个功能。具体来说，我们可以定义一个函数oneSumCloset，它接受五个参数：数组nums、两个整数i和j表示当前考虑的两个数在数组中的位置、一个整数start和end表示在数组中查找的范围、以及目标值target。
在oneSumCloset函数中，我们首先处理边界情况。如果start等于i或j，则将start加1；如果end等于i或j，则将end减1。接下来，我们判断start和end的关系。如果它们相等，说明已经找到了与target最接近的数，直接返回该数即可。如果它们相差为1，说明只有一个数与target最接近，比较这两个数与target的差值，返回差值较小的那个数。否则，我们计算中间位置middle，并根据nums[middle]与target的大小关系来更新查找范围。然后递归调用oneSumCloset函数，继续查找。
在主函数threeSumClosest中，我们初始化最小值为0，并设置一个布尔变量hasMin为false，用于标记是否已经找到了与目标值最接近的三个数。然后使用两层循环遍历数组中的每两个数的组合，计算它们的和，记为twoSum。接着，我们调用oneSumCloset函数，找到与twoSum最接近的数，记为restClost。最后，我们计算这三个数的和newValue，并与当前最小值进行比较。如果找到了更接近目标值的三个数，更新最小值和hasMin。
当两层循环结束后，返回最小值minValue即可。

代码思路

它包含两个方法：oneSumCloset和threeSumClosest。

oneSumCloset方法：这个方法用于在一个有序数组中找到与给定目标值最接近的数。它接受6个参数：一个整数数组nums，两个整数i和j，表示要搜索的范围，以及三个整数start、end和target，分别表示搜索的起始位置、结束位置和目标值。

方法首先检查start和end是否等于i或j，如果是，则将它们分别加1或减1。

 // 在数组nums中，从i到j范围内查找与target最接近的数int oneSumCloset(int[] nums, int i, int j, int start, int end, int target) {if (start == i || start == j) // 如果start等于i或j，则将start加1start = start + 1;

然后，根据start和end的值进行不同的处理。如果start和end相等，说明已经找到了与目标值最接近的数，直接返回该数。如果start和end相差1，说明只有一个数与目标值最接近，比较这两个数与目标值的差值，返回差值较小的那个数。否则，计算start和end的中间位置middle，并根据nums[middle]与目标值的大小关系，更新start或end的值。

if (end == i || end == j) // 如果end等于i或j，则将end减1end = end - 1;if (start == end) { // 如果start等于end，说明已经找到了与target最接近的数，直接返回该数return nums[start];} else if (end == start + 1 || end == start - 1) { // 如果end等于start+1或start-1，说明只有一个数与target最接近，比较这两个数与target的差值，返回差值较小的那个数if (Math.abs(nums[end] - target) > Math.abs(nums[start] - target)) {return nums[start];} else {return nums[end];}} else { // 如果以上条件都不满足，说明需要继续查找int middle = (int) Math.floor((start + end) / 2); // 计算中间位置if (nums[middle] > target) { // 如果中间位置的数大于target，说明目标数在左半部分，将end更新为middleend = middle;} else { // 如果中间位置的数小于等于target，说明目标数在右半部分，将start更新为middlestart = middle;}

最后，递归调用oneSumCloset方法，继续在更新后的范围内查找与目标值最接近的数。

   return oneSumCloset(nums, i, j, start, end, target); // 递归调用oneSumCloset方法，继续查找

threeSumClosest方法：这个方法用于在一个有序数组中找到三个数之和最接近给定目标值的组合。它接受两个参数：一个整数数组nums和一个整数target，分别表示输入的数组和目标值。

方法首先对数组nums进行排序。然后，使用两层循环遍历数组中的每对数，计算它们的和作为twoSum，并计算剩余的目标值rest。接着，调用oneSumCloset方法，在剩余的数组元素中查找与rest最接近的数作为restClost。

 // 在数组nums中，查找三个数之和最接近target的组合public int threeSumClosest(int[] nums, int target) {Arrays.sort(nums); // 对数组进行排序int minValue = 0; // 初始化最小值为0boolean hasMin = false; // 初始化hasMin为false，表示还没有找到最小值for (int i = 0; i < nums.length - 2; i++) { // 遍历数组中的前n-2个数for (int j = i + 1; j < nums.length - 1; j++) { // 遍历数组中的第i+1个数到倒数第二个数int twoSum = nums[i] + nums[j]; // 计算两个数之和int rest = target - twoSum; // 计算剩余的目标值int restClost = oneSumCloset(nums, i, j, j + 1, nums.length - 1, rest); // 在剩余的数组元素中查找与rest最接近的数

将restClost与twoSum相加得到新的值newValue。接下来，判断是否已经找到了最小值minValue，如果没有找到，则将newValue赋值给minValue，并将hasMin设置为true。如果已经找到了最小值minValue，则比较newValue与minValue与目标值的差值d1和d2，如果d1大于d2，则将newValue赋值给minValue。

  int newValue = restClost + twoSum; // 计算新的值if (!hasMin) { // 如果还没有找到最小值minValue = newValue; // 更新最小值hasMin = true; // 将hasMin设置为true，表示已经找到了最小值} else { // 如果已经找到了最小值int d1 = Math.abs(minValue - target); // 计算当前最小值与目标值的差值int d2 = Math.abs(newValue - target); // 计算新值与目标值的差值if (d1 > d2) { // 如果当前最小值的差值大于新值的差值minValue = newValue; // 更新最小值}}

最后，返回minValue作为结果。

return minValue; // 返回最小值

参考代码

class Solution {int oneSumCloset(int[] nums, int i, int j, int start, int end, int target) {if (start == i || start == j)start = start + 1;if (end == i || end == j)end = end - 1;if (start == end) {return nums[start];} else if (end == start + 1 || end == start - 1) {if (Math.abs(nums[end] - target) > Math.abs(nums[start] - target)) {return nums[start];} else {return nums[end];}} else {int middle = (int) Math.floor((start + end) / 2);if (nums[middle] > target) {end = middle;} else {start = middle;}return oneSumCloset(nums, i, j, start, end, target);}}public int threeSumClosest(int[] nums, int target) {Arrays.sort(nums);int minValue = 0;boolean hasMin = false;for (int i = 0; i < nums.length - 2; i++) {for (int j = i + 1; j < nums.length - 1; j++) {int twoSum = nums[i] + nums[j];int rest = target - twoSum;int restClost = oneSumCloset(nums, i, j, j + 1, nums.length - 1, rest);int newValue = restClost + twoSum;;if (!hasMin) {minValue = newValue;hasMin = true;} else {int d1 = Math.abs(minValue - target);int d2 = Math.abs(newValue - target);if (d1 > d2) {minValue = newValue;}}}}return minValue;}
}

求公式的值

题目

求 1-1/2!-1/3! -… -1/10!

解题思路

首先，我们需要计算阶乘。在给定的代码中，已经有一个名为jiecheng的方法用于计算阶乘。我们可以使用这个方法来计算1-1/2!-1/3! -… -1/10!的值。
在sum方法中，我们需要遍历从1到n的所有整数。对于每个整数i，我们需要计算1/i!并将其累加到总和中。同时，我们需要更新变量s的值，使其在每次迭代时取反。
最后，在main方法中，我们调用sum方法并传入参数n=10，然后输出结果。

代码思路

这段代码是一个Java程序，用于计算一个数列的和。该数列由以下公式生成：

sum = 1/n! + (-1)^n / (n-1)! + ... + 1/1!

程序中定义了两个方法：jiecheng和sum。

jiecheng方法用于计算阶乘（factorial），即从1到给定整数n的所有正整数的乘积。它使用了一个循环来逐个乘以从1到n的整数，并将结果存储在变量s中。最后，该方法返回计算得到的阶乘值。

// 定义一个静态方法jiecheng，接收一个整数n作为参数，返回n的阶乘public static double jiecheng(int n) {double s = 1; // 初始化变量s为1// 使用for循环计算n的阶乘for (int i = 1; i <= n; i++) {s *= i; // 将s乘以i}return s; // 返回计算结果

sum方法用于计算数列的和。它使用了一个循环来迭代从1到n的每个整数。在每次迭代中，它将当前项的值累加到变量sum中。每一项的值由公式1/n! + (-1)^n / (n-1)!计算得出。其中，(-1)^n表示交替的符号，(n-1)!表示n-1的阶乘。最后，该方法返回计算得到的数列和。

// 定义一个静态方法sum，接收一个整数n作为参数，返回数列的和public static double sum(int n) {double sum = 0.0; // 初始化变量sum为0.0int s = 1; // 初始化变量s为1// 使用for循环计算数列的和for (int i = 1; i <= n; i++) {sum += s / jiecheng(i); // 将s除以i的阶乘加到sum上s = -s; // 将s取反}return sum; // 返回计算结果}

在main方法中，程序将整数n设置为10，并调用sum方法来计算数列的和。然后，它将结果打印到控制台上。

// 定义一个主方法main，程序的入口点public static void main(String[] args) throws Exception {int n = 10; // 定义变量n为10double ss = sum(n); // 调用sum方法计算数列的和，并将结果赋值给变量ssSystem.out.println(ss); // 输出数列的和}

参考代码

public class TEST {public static double jiecheng(int n) {double s = 1;for (int i = 1; i <= n; i++)s *= i;return s;}public static double sum(int n) {double sum = 0.0;int s = 1;for (int i = 1; i <= n; i++) {sum += s / jiecheng(i);s = -s;}return sum;}public static void main(String[] args) throws Exception {int n = 10;double ss = sum(n);System.out.println(ss);}
}