树的基本性质
- ⭐️计算树的总结点与叶结点数
- 💫性质1
- 💫性质2
- 💫例题1
- 💫例题2
⭐️计算树的总结点与叶结点数
💫性质1
性质1 树中的结点数等于所有结点的度数之和加1
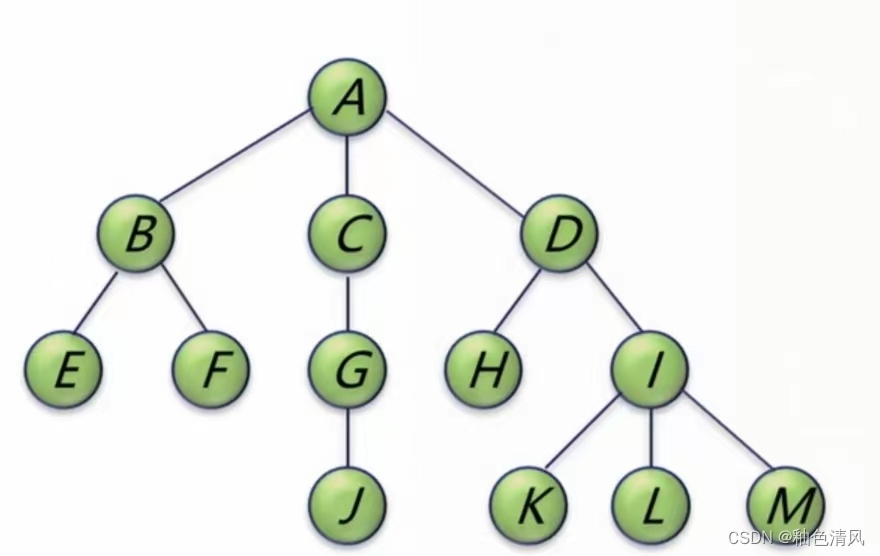
例如上面这棵树,A的孩子为B、C、D,A的度数为3;B的孩子为E、F,B的度数为2;C的孩子为G,C的度数为1;D的孩子为H、I,D的度数为2…
结点数=A的度数+B的度数+C的度数+D的度数+…+J的度数+K的度数+L的度数+M的度数+1
=(B+C+D)+(E+F)+G+(H+I)+…+0+0+0+0+1
也就是结点数等于每个结点的孩子树之和(度之和)再加1,这个1就是根节点。
总结点数:n=13;
树的度:m=3;
n0(度为0的结点数)=7;
n1(度为1的结点数)=2;
n2(度为2的结点数) =2;
n3(度为3的结点数)=2;
n = 7 ∗ 0 + 2 ∗ 1 + 2 ∗ 2 + 2 ∗ 3 + 1 n=7*0+2*1+2*2+2*3+1 n=7∗0+2∗1+2∗2+2∗3+1
💫性质2
性质2 结点表示个数:n为总结点个数, n i {n_i} ni为度为i(0≤i≤m)的结点个数,则 n = n 0 + n 1 + . . . + n m {n=n_0+n_1+...+n_m} n=n0+n1+...+nm

对于上面这棵树
总结点树 n=13;
这树的度数m=3;
n 0 {n_0} n0=7;
n 1 {n_1} n1=2;
n 2 {n_2} n2=2;
n 3 {n_3} n3=2;
n = n 0 + n 1 + n 2 + n 3 n={n_0+n_1+n_2+n_3} n=n0+n1+n2+n3
对于上面两种计算树的结点的方法,我认为一个是从一个结点本身出发,计算它自己本身;另一种是从它的孩子出发,计算之和 ,但由于这样树的根节点没有被纪录,所以不要忘了加1。
💫例题1
一颗树度为4的树T中,若有20个度为4的结点,10个度为3的结点,1个度为2的结点,10个度为1的结点,则树T的叶子结点个数为()
A.41 B.82 C.113 D.122
分析:
从两种角度出发:
从结点自身:
总结点 n = 20 + 10 + 1 + 10 + n 0 n=20+10+1+10+n_0 n=20+10+1+10+n0
从结点的孩子:
总结点 n = 20 ∗ 4 + 10 ∗ 3 + 1 ∗ 2 + 10 ∗ 1 + 1 n=20*4+10*3+1*2+10*1+1 n=20∗4+10∗3+1∗2+10∗1+1
联立上面两式,可以解得 n 0 = 82 n_0=82 n0=82
💫例题2
已知一棵树度为m的树中有 n 1 n_1 n1个度为1的结点, n 2 n_2 n2个度为2的结点,…, n m n_m nm个度为m的结点,问该树中有多少个叶子结点?
设总结点n
则 n = n 1 + n 2 + . . . + n m + n 0 n=n_1+n_2+...+n_m+n_0 n=n1+n2+...+nm+n0
且 n = 1 ∗ n 1 + 2 ∗ n 2 + 3 ∗ n 3 + . . . + m ∗ n m + 1 n=1*n_1+2*n_2+3*n3+...+m*n_m+1 n=1∗n1+2∗n2+3∗n3+...+m∗nm+1
联立解得, n 0 = n 2 + 2 n 3 + 3 n 4 + . . . + ( m − 1 ) n m + 1 n_0=n_2+2n_3+3n_4+...+(m-1)n_m+1 n0=n2+2n3+3n4+...+(m−1)nm+1