栈的概念:
栈:
一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端 称为栈顶,另一端称为栈底。
栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。
- 入栈:栈的插入操作叫做 进栈/压栈/入栈,进入数据在栈顶 。
- 出栈:栈的删除操作叫做出栈。出数据也在栈顶。
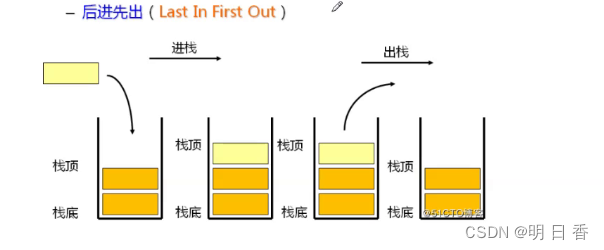
后进先出:
入栈和出栈遵循后进先出原则,即处在栈顶的数据先出栈,不处在栈顶的数据不能出栈,简单来说,就是只有处在栈顶的数据才能出栈。
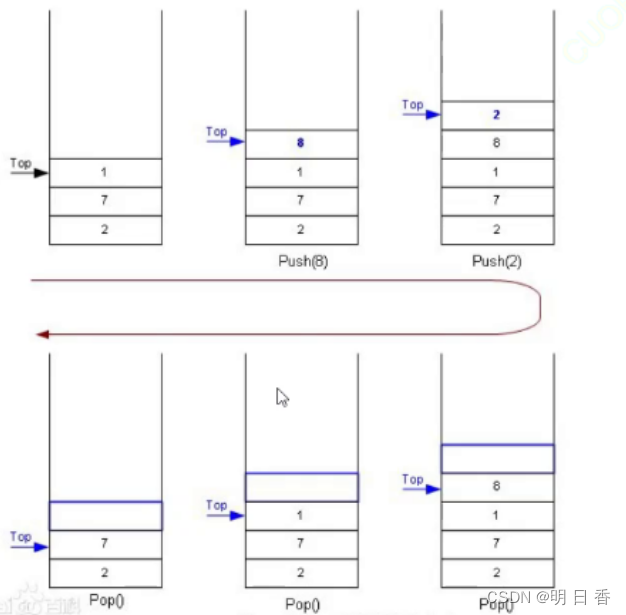
数据模型的转化:
栈分为两种,一种是数组栈,另一种是链式栈,且注意,栈是不分头尾概念的,只分栈顶和栈底
数组栈:

对于数组栈,数组的本质是顺序表,如果需要实现数组栈,则相当于实现顺序表。
且因为栈只分栈顶和栈底,又因为顺序表的尾插操作和尾删操作和其他插入删除操作更为便捷,于是选择顺序表的左边为栈底,顺序表的右侧为栈顶。
链式栈:
对于链式栈,其实就是链表结构的栈,而链表结构的栈分为两种,一种是双向链表,另一种是单链表。
双向链表栈:
双链表具有指向前一个节点的前驱指针和指向后一个节点的后继指针,所以对于栈顶和栈底的划分并不是非常的重要。且如若栈的数量过多,指针也的过多,会导致一定的浪费,所以双向链表模式的栈并不常用。
单链表栈:
对于单链表而言,如果栈顶是尾节点,那么进行出栈就是尾删,但是单链表的尾删十分麻烦,需要头节点进行遍历。
于是便将单链表的栈顶变为头节点,栈底变为尾节点
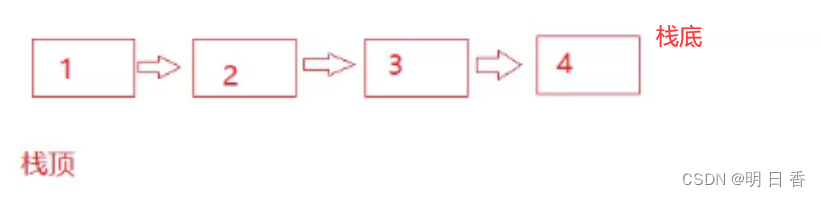
比较:在链式和数组栈中,最佳的是数组栈,虽然偶尔需要扩容。
数组栈的实现:
从前文得知,数组栈的本质是顺序表,且因为栈是只能从栈顶进行出入,所以数组栈其实就是拥有尾删、尾插、初始化、销毁功能的顺序表。
顺序表:顺序表的简单介绍_明 日 香的博客-CSDN博客
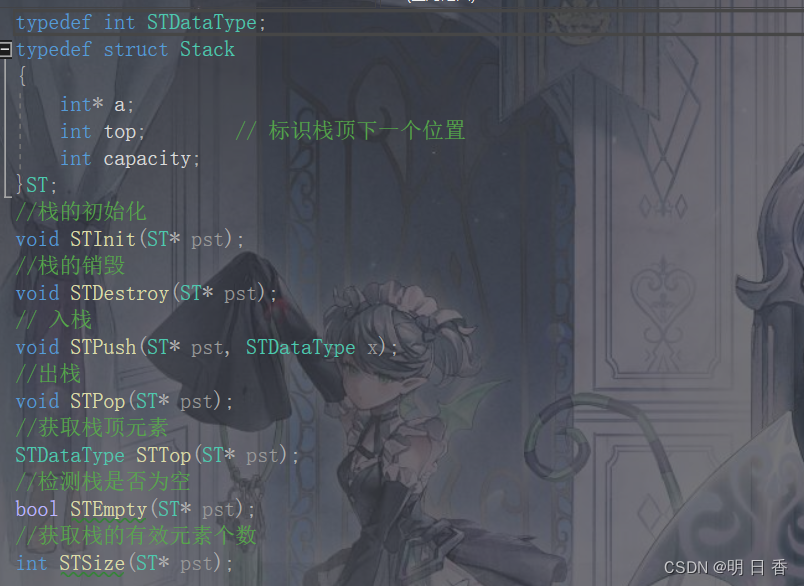
关于top:
- 对于栈的结构体内部,一切都与顺序表的内部十分的相似,不论是存储 栈的地址 a ,还是表示栈的空间大小的capacity 。
- 当然,top 并不是和顺序表中的size 一样表示有效个数的大小。
top 可以有两种表示,一种是表示为栈顶的位置,另一种是表示为栈顶的后面一个元素的位置。
第一种:表示栈顶位置
如果top表示为栈顶的位置,那么在进行初始化的时候,top就不能设置为 top==0
- 0表示数组的下标。
假设,top == 0 而 top 又定义为栈顶所在的位置,那么根据我们的初始化,最初的数组栈是没有栈存在的。
而top 又在下标为0的位置,但是,当我们入栈后,栈顶和栈底都在下标为0的位置。
于是,这就产生了冲突,因为当没有任何栈存在时,top在0的位置,但是当进入一个栈后,top还在0的位置。
那么,top == 0 时,究竟有没有栈的存在呢?这就像薛定谔的猫一样,存在异议。
- 所以,面对这种问题,如果需要将top定义为栈底的位置,那么我们就需要将top的初始值设定为 top == -1
第二种:表示栈顶后的下一个位置。
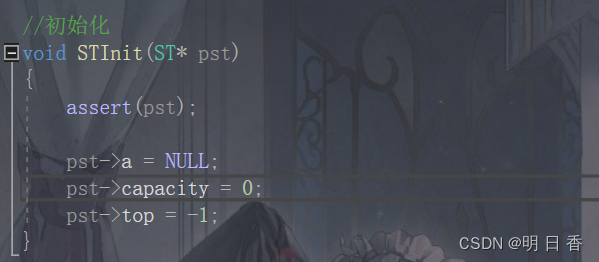
如果top表示的是 栈顶的下一个位置,那么在初始化时,top==0 可以表示为下一个栈入栈后,栈顶的位置处在下标为0的位置。
关于扩容:
数组栈扩容的原因和顺序表一样,空间的不足需要进行扩容,且因为需要连续的数组,所以当所处的空间不能满足扩容后连续的条件,会进行复制数据转移到新的空间足够,且能连续的空间中。
- 而对于扩容而言,top 也与扩容有着重要的关系。
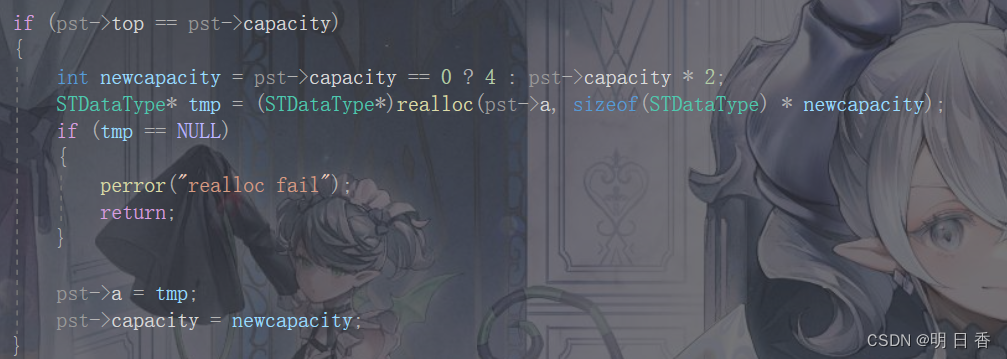
如果初始化中,top == 0 那么我们需要扩容空间的条件则是 top == capacity
- 也就是,栈顶 的下一个位置的下标等于当前空间的大小时,则表明我们需要进行扩容。
因为 top == 0 表示的意思是下一个入栈的节点 的下标是0 ,又因为数组的下标是从0开始的,所以得出结论,如果空间满了,栈顶因为下标的缘故,栈顶所处在的下标数字比空间大小小一,但空间确是满的!
那么栈顶所处的位置如果下一个位置的下标和空间大小一样,则表明当前空间不够了!
与之相反,如果top == -1 ,则需要top+1才能满足以上的条件。
入栈(尾插):
和顺序表一样,在top的位置插入数据——注意这里的top 表示栈顶的下一个位置下标。

出栈(尾删):
和顺序表的尾删一样,只需要让栈顶减一即可。
同时,出栈的前提是需要有栈的存在,如果top ==0或则top<0 都表示,当前是没有栈存在的,因为top == 0是下一个栈的下标是0,所以top==0是没有栈,而top也是如此,表示的是当前的栈顶是-1负数,表明了没有栈存在。

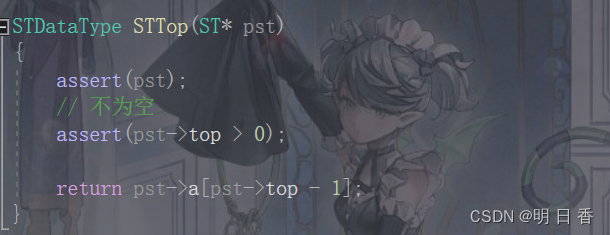
获取栈顶元素:
初始化 top==0 ,top表示为栈顶后一个位置下标时写法: