关于哈夫曼编码,想必大家都很清楚,这里来讲解一下他的详细证明方法。代码的话就不给了网上一大堆,我再给也没什么意思,这里主要讲明白正确性的证明。我将采取两种方法进行证明,一种常规的方法,还有一种采取强数学归纳法证明。如果你已经了解了哈夫曼可以直接去看证明的正确性
(由于画图软件问题,图中有一些竖线忽略即可)
这里写目录标题
- 一:编码
- 1.固定长度的编码
- 2.变长的编码
- 3.非前缀的变长编码
- 4.变长与定长的编码比较
- 二:编码与二叉树的关系
- 1.定长的编码与树
- 2.变长的编码与树
- 前缀编码
- 非前缀编码
- 三:哈夫曼算法的描述
- 1.哈夫曼算法解决的问题
- 2.哈夫曼算法的步骤
- 四:哈夫曼算法的正确性证明
- 1.第一种证明方法(常规的方法)
- (1)最优子结构性质的证明
- (2)贪心选择性质的证明
- (3) 这两个性质的关系
- 2.第二种证明方法(数学归纳证明,采用强归纳法)
一:编码
1.固定长度的编码
对于编码问题最先想到的就是固定长度的编码例如
| 字母 | 编码 |
|---|---|
| A | 00 |
| B | 01 |
| C | 10 |
| D | 11 |
2.变长的编码
这时我们就要想了是不是还有一个更优的编码,既然有定长的编码,自然的就会想到变长的编码,什么是变长的编码呢
| 字母 | 编码 |
|---|---|
| A | 0 |
| B | 1 |
| C | 01 |
| D | 10 |
这种就是边长的编码,但是这种编码又有一种问题:
如果我们的编码是0110,它对应的字母是什么呢?
我们发现它对应多种的字母如:ABBA,ABD
那这种编码就没有意义了,因为这种编码我们是没有办法解码的,解不了码就不知道传输的信息是什么了,自然也就没有意义了。
这种情况什么导致的呢,是因为A的编码是C的编码的前缀这就导致了二义性。
3.非前缀的变长编码
既然是因为前缀导致了二义性,那就自然而然的会采用非前缀编码非前缀编码大家肯定都知道是什么意思了,这里来举一个例子:
| 字母 | 编码 |
|---|---|
| A | 0 |
| B | 10 |
| C | 110 |
| D | 111 |
这种还会产生歧义吗?:
随便写一个编码
1010111:BBD
10111110: BDC
发现除了一些没有的编码比如101这种没有对应的坏码(这里不是哈夫曼的内容,那是检错校验的内容) 外其他的都是可以解码的。
4.变长与定长的编码比较
对于定长的编码的平均长度肯定就是固定的了,对于变长的编码就与编码的长度和他出现的概率有关了:例如上面的定长的平均编码长度是2,变长的话就先假设概率依次对应的是0.6,0.2,0.1,0.1;他的平均长度就是
∑ x ∈ {字母的集合} p ( x ) ⋅ len ( x ) = 0.6 ∗ 1 + 0.2 ∗ 2 + 0.1 ∗ 3 + 0.1 ∗ 3 = 1.6 \sum_{x \in \text{{\{字母的集合\}}}} p(x) \cdot \text{{len}}(x) = 0.6 * 1+0.2 * 2+0.1*3+0.1 * 3=1.6 ∑x∈{字母的集合}p(x)⋅len(x)=0.6∗1+0.2∗2+0.1∗3+0.1∗3=1.6
发现变长的比定长的要小。
二:编码与二叉树的关系
1.定长的编码与树
根据上面的定长编码,画一个二叉树
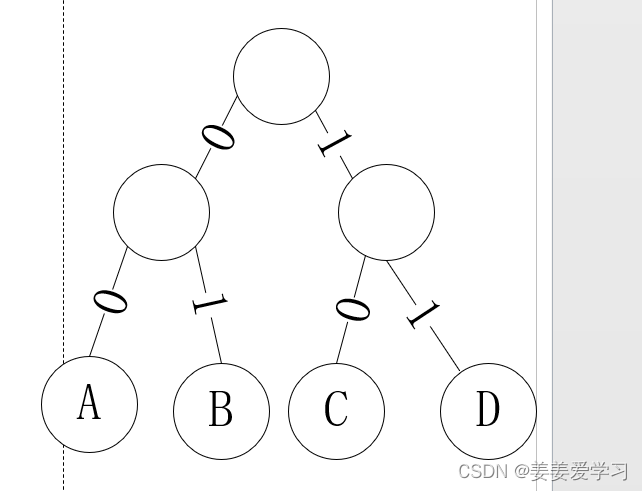
二叉树向左为0向右为1
2.变长的编码与树
前缀编码

非前缀编码

通过这几个例子我们发现二叉树与编码是存在一一对应的关系的。
三:哈夫曼算法的描述
1.哈夫曼算法解决的问题
哈夫曼是为了解决最优的非前缀编码问题,即平均编码长度的最小值,通过前面的例子可知编码的长度与树的深度是一样的。所以我们希望
∑ x ∈ {树的叶子节点} p ( x ) ⋅ len ( x ) \sum_{x \in \text{{\{树的叶子节点\}}}} p(x) \cdot \text{{len}}(x) ∑x∈{树的叶子节点}p(x)⋅len(x) 最小(注释:树的平均深度最小那么对应的平均编码长度就最小)
2.哈夫曼算法的步骤
假设给出的字母集合每一个字母都是一个单独的树,这些树组成集合TG,且对应于x∈TG设他的概率为p(x)
step 1: 从TG中选择概率最小的树a,和概率次小的树b合并。
step 2: 把step 1得到的新的树加入TG,并且把其概率设为p(a)+p(b),然后把a,b从TG中划掉
step 3: 重复上述步骤直到只剩下一棵树
所以哈夫曼就是把一个森林维护成树的过程
这里使用上述的非前缀编码举例子:
| 字母 | 概率 |
|---|---|
| A | 0.6 |
| B | 0.2 |
| C | 0.1 |
| D | 0.1 |
TG集合为:
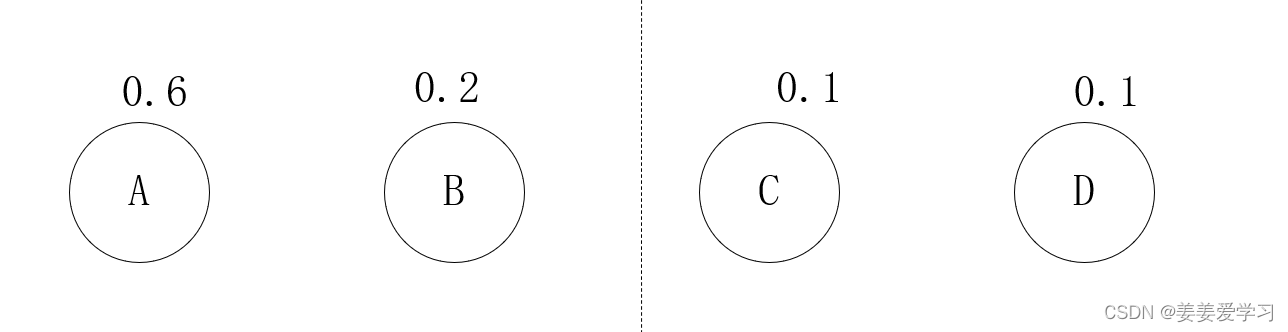
(中间那条线为画图软件问题,无特殊含义)
step 1: 从TG中选择概率最小的树C,和概率次小的树D合并。
step 2: 把step 1得到的新的树加入TG,并且把其概率设为p(a)+p(b),然后把a,b从TG中划掉
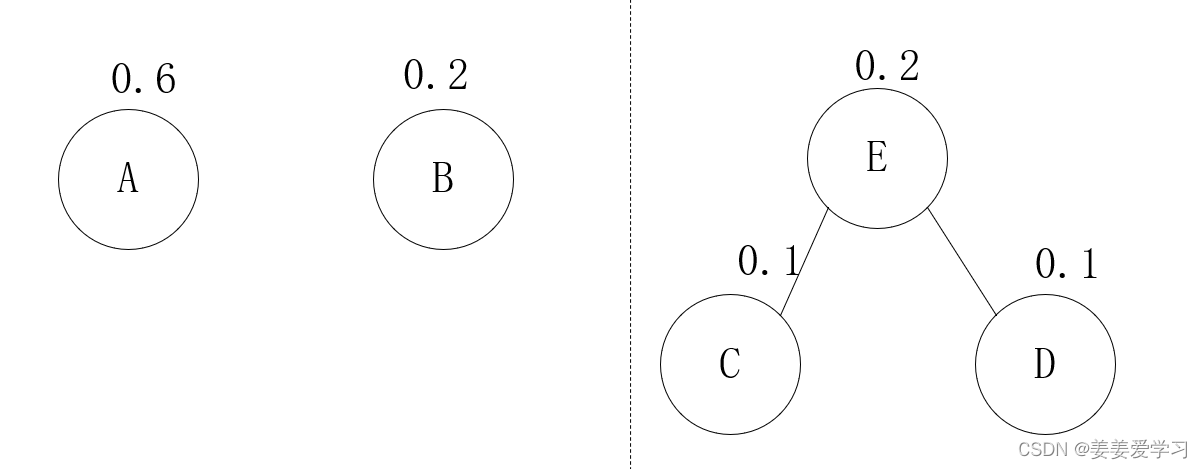
TG变成了A,B,E树的集合C,D变成了E的子节点
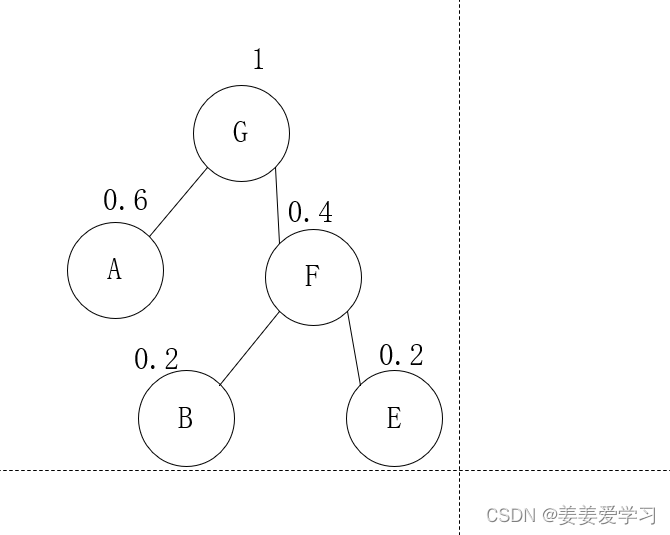
step 3重复上述步骤:选择最小的合并,并且划去被合并的(最小的B,次小的E)
TG变成了A F的集合:
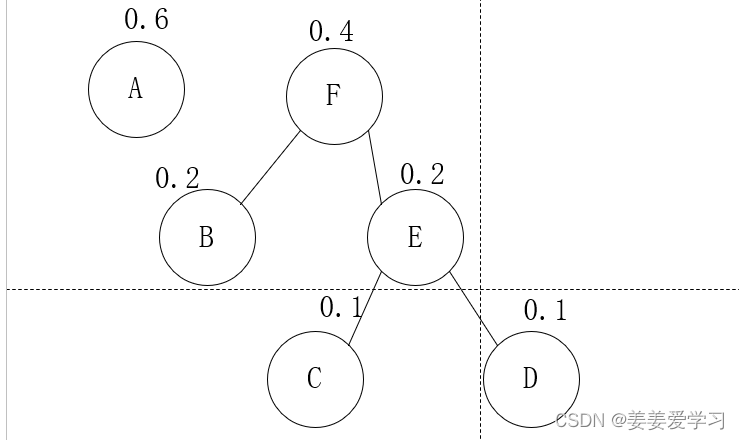
然后继续
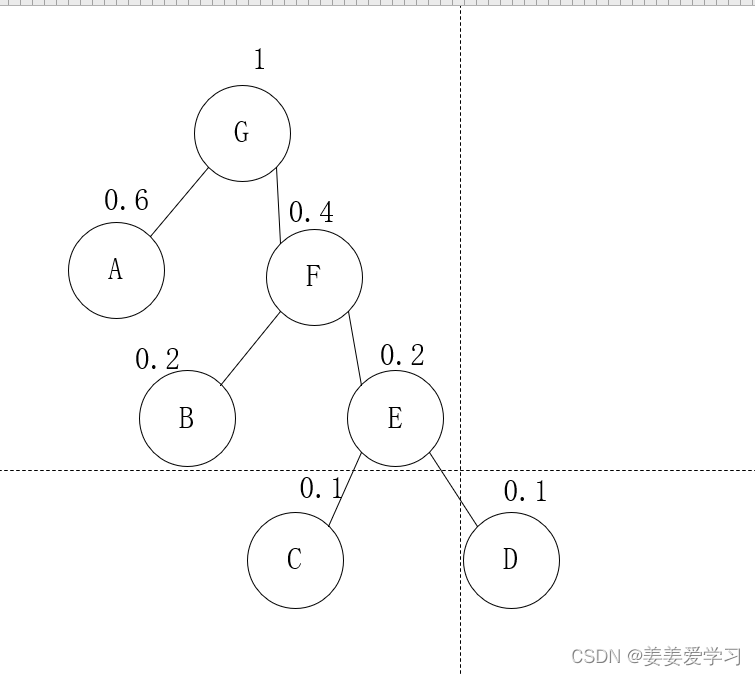
这时TG就只有一棵树了,算法结束
然后看一下他们的编码,(二叉树向左是0向右是1)
| 字母 | 编码 |
|---|---|
| A | 0 |
| B | 10 |
| C | 110 |
| D | 111 |
以上就是哈夫曼的所有步骤
四:哈夫曼算法的正确性证明
接下来就到了重头戏,正确性的证明
证明之前为了方便证明先说明一些符号的含义:
AG: 代表字母的集合
TG: 代表字母对应的树的集合(即每一个字母都看做一棵树,和上面的含义一样)
TAG: 字母最后构成的平均深度最小的二叉树
|TAG|: 表示他的最小平均深度
**a,b:**字母集合中概率最小和次小的字母
Ta: TG中概率最小的树
Tb: TG中概率次小的树
1.第一种证明方法(常规的方法)
贪心的证明往往就是证明贪心选择性质,和最优子结构性质然后就可以得到该算法是正确的
先确定一下子问题是什么:

他的子问题就是把最小的和次小的字母合成一个字母之后的树,合并之后的字母的概率为p©+p(D)
(1)最优子结构性质的证明
最优子结构就是原问题的最优解是子问题的最优解构成的:
子问题与原问题的关系是什么呢?
设T原表示原来的树
T合表示合并之后的树
根据上面的子问题图解可知,T合是T原的子问题
因为T原中的最小概率的节点a和次小的节点b比T合的节点c的深度要大一,所以
|T原|=|T合|+p(a)+p(b)
(例如上图的C,D合并成E之后树的平均深度就少了p( C)+p(D) ( @注解:算平均深度的时候就是只有叶节点,叶节点才是我们想要编码的字母)
设|T原|是最优解,如果子问题最优的不是|T合|而是|T合*|那么|T合 * |+p(a)+p(b)才是最优的,与|T原|是最优解产生矛盾,所以最优子结构得证
(2)贪心选择性质的证明
既然它是贪心选择,那么只要最开始的时候合并的两个树是Ta,Tb那就说明他是以贪心选择开始的(即TAG的最深的两个节点就是节点a,b)
设一开始合并的是Tx,Ty:
那就有三种情况
第一种情况Tx,Ty就是Ta,Tb
第二种情况Tx,Ty不是Ta,Tb
第三种情况Tx,Ty中只有一个Ta或Tb
对于第一种情况,那么他就是以贪心选择开始的;
对于第二三种情况证明是类似的,这里证明更难的第二种:
那就把它换成Ta,Tb构成新的一棵树TAG*:换之后的影响是什么呢?考虑一下:
因为除了Tx,Ty,Ta,Tb其他的节点都是不变的所以只需要考虑这四个即可
|TAG| - |TAG *|=
p(x)(x在TAG的深度 - x在TAG*的深度)+
p(y)(y在TAG的深度 - y在TAG*的深度) +
p(a)(a在TAG的深度 - a在TAG*的深度) +
p(b)(b在TAG的深度 - b在TAG*的深度)
( 因为x,y与a,b交换所以他们的深度也就交换了即深度x=深度a 深度y=深度b或则 深度y=深度a 深度x=深度b其实这两个是一种情况深度x=深度a 深度y=深度b也可以表示 深度y=深度a 深度x=深度b因为我们取的下x,y都是随机的,x与y可以是任何值,所以说他俩交换之后,x仍然是x,y仍然是y)
这里计算时设a,x交换b,y交换
这样上面的式子可以化为
|TAG| - |TAG *|=
p(x)(a在TAG*的深度 - x在TAG*的深度)+
p(y)(b在TAG*的深度 - y在TAG*的深度) +
p(a)(x在TAG*的深度 - a在TAG*的深度) +
p(b)(y在TAG*的深度 - b在TAG*的深度)
={p(x)-p(a)}*(a在TAG *的深度 - x在TAG 的深度)+{p(y)-p(b)}(b在TAG *的深度 - y在TAG *的深度)
>=0
*(注解:为什么会大于等于零,因为p(a),p(b)是最小的,并且在TAG 中a,b节点是最深得)
又因为TAG是最优解,所以有|TAG| - |TAG *|<=0
所以可以得到|TAG| = |TAG *|,得证TAG *也是一个最优解
所以他总是以贪心选择开始,并且选择完之后又出现一个类似的子问题,还是重复上述的步骤。
(3) 这两个性质的关系
这里特别说明一下贪心选择性质:我看网上的定义都是这样的经过一系列的局部最优选择最后可以构成整体最优解。我感觉这时不准确的,这不就是贪心的定义吗,这样和贪心有啥区别呢?我的理解是当前的局部最优选择可以构成该问题的最优解(注:我说的是该问题不是整体问题,如果他再满足最优子结构那就是满足贪心算法了,后面给出公式后进行详解)
满足这两个性质之后就可以说他是满足贪心的
如果只满足贪心选择,就只能说明这一步选择是最优解的一部分,但是对于选择完之后剩下的子问题,我们不能确定是不是他的最优解构成原问题的最优解。
如果只满足最优子结构那么他就不能说明他是贪心选择得来的。
其实就是一个等式关系:
原问题最优解=这一步的局部最优解+选择完之后子问题的最优解。
然后子问题的最优解又可以看作原问题最优解,再次使用上述公式求得。
(有了这个等式之后我们再去理解一下,我说的贪心选择性质:当前的局部最优选择可以构成该问题的最优解。回想一下我们证明贪心选择性质时的方法,我们就是证明了当前问题的最优解是由贪心选择开始的,然后又说明子问题是类似的,都是由贪心选择开始的。然后他又满足最优子结构性质,这样就可以把公式原问题最优解=这一步的局部最优解+选择完之后子问题的最优解。化为原问题最优解=这一步的局部最优解+选择完之后子问题的局部最优解+子问题选择完局部最优解之后剩下的子问题的最优解(即该子问题的子问题的最优解)。 它可以一直化简下去直到没有子问题,这样我们发现我们每一次都是选择的局部最优解最后构成整体的最优解。可见我们获得了正确答案,这样我对于贪心选择性质的定义的猜想也就加以证明了)
2.第二种证明方法(数学归纳证明,采用强归纳法)
————未完待续————