什么是AVL树？

AVL树又称平衡二叉搜索树，相比与二叉搜索树多了平衡的概念，为什么要有平衡二叉搜索树呢？因为二叉搜索树可能会出现退化现象，导致左右子树高度相差较大，甚至退化成单链表的形式，因此我们提出了平衡二叉搜索树，可以有效地解决高度相差过大的情况，平衡二叉搜索树要求任意节点的左右子树高度相差不大于1.

平衡因子

为了解决高度差问题，我们在每一个节点中添加了平衡因子变量，这个变量用于记录该节点的左右子树的高度差。
若规定平衡因子等于右子树高度减去左子树高度，那么如果新增节点的位于当前节点的左侧那么该节点平衡因子-1，如果位于该节点的右侧，则该节点平衡因子+1，并且一直向上修改平衡因子，直到某个节点平衡因子为0，或者到根节点，或者需要进行调整

Node节点

template <class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;//pair是库中的类,包含first和second两个成员变量AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;//blance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};

我们规定平衡因子等于右子树高度减去左子树高度

插入

平衡二叉搜索树也是二叉搜索树，因此它的插入和二叉搜索树类似，都是找到一个合适的节点进行插入，不同的是这棵树要保证每个节点的平衡因子不大于1，因此我们在插入后可能需要对该树的节点进行调整。
需要调整的情况有以下四种：分别是

新节点插入较高左子树的左侧

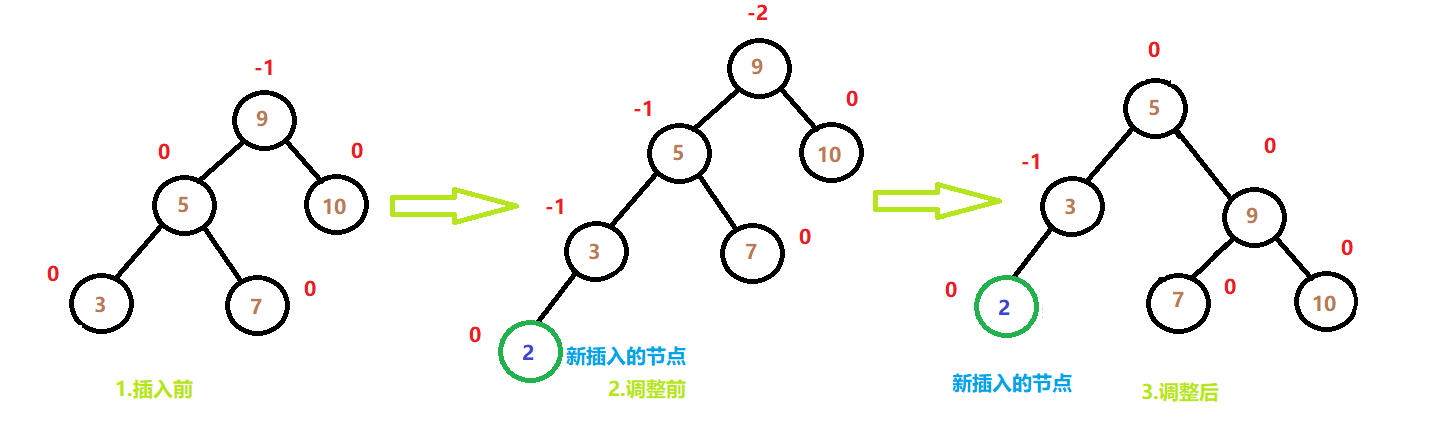
情况1：

情况2

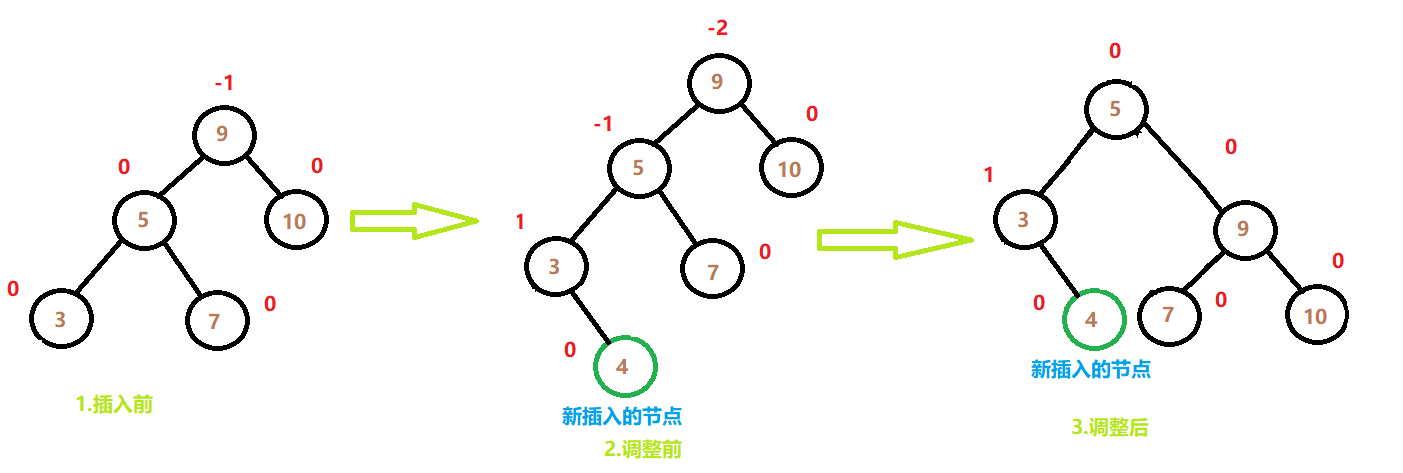
上面两种情况的处理方式是一样的，因为这两种情况都属于较高子树的左边，以图为例，5和10所在位置分别是不平衡节点9的左右子树，而新插入的节点都是位于左子树的根节点5的左侧

思路：如果新插入的节点位于不平衡节点的左子树的左侧，要想让不平衡节点变平衡，就要让高的一侧子树高度-1，低的一侧子树高度+1，这样就可以使得原本高度差为2的左右子树的高度差变为0，同时还要保证二叉树的性质不被破坏，所以还要对6进行处理。
右单旋：不平衡节点以及它的右子树进行，绕不平衡节点的左孩子旋转90度。
右单旋是指不平衡节点以及它的右子树进行旋转

//新节点插入较高左子树的左侧----左左: 右单旋
void RotateR(Node* parent)
{++_rotateCount;Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;/if (curright){//parent->_right = curright;curright->_parent = parent;}cur->_right = parent;Node* ppnode = parent->_parent;parent->_parent = cur;//if (parent = _root)if(ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (parent == ppnode->_left){//cur = ppnode->_left;ppnode->_left = cur;}else{//cur = ppnode->_right;ppnode->_right = cur;}cur->_parent = ppnode;}cur->_bf = parent->_bf = 0;
}

最后不要忘记把新插入节点和那个不满足平衡因子的左孩子的平衡因子都置为0

新节点插入较高左子树的右侧

新插入节点位于7的左右两侧都属于同一种情况，这里就不做演示了。
先把不满足平衡因子的节点的左孩子进行左旋转，在对不满足平衡因子的节点进行右旋转。

//新节点插入较高左子树的右侧---左右:先左单旋再右单旋
void RotateLR(Node* parent)//先左旋再右旋
{Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){curright->_bf = 0;cur->_bf = -1;parent->_bf = 0;}else if (bf == -1){curright->_bf = 0;cur->_bf = 0;parent->_bf = 1;}else{assert(false);}
}

调整完之后不要忘记对旋转节点的平衡因子进行调整

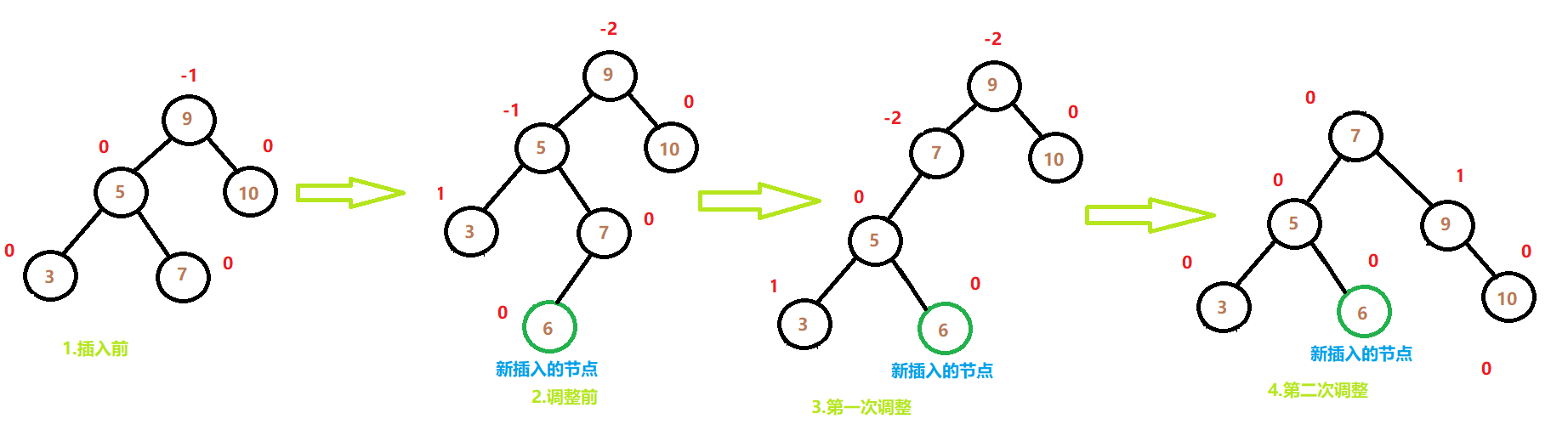
新节点插入较高右子树的左侧

插入到较高右子树左侧与插入到较高左子树右侧对称，因此调整方式恰好相反，因此是先右旋再左旋

//新节点插入较高右子树的左侧---右左:先右单旋再左单旋
void RotateRL(Node* parent)
{
Node* cur = parent->_right;
Node* curleft = cur->_left;
int bf = curleft->_bf;RotateR(parent->_right);
RotateL(parent);if (bf == 0)
{parent->_bf = 0;cur->_bf = 0;curleft->_bf = 0;
}
else if (bf == 1)
{curleft->_bf = 0;cur->_bf = 0;parent->_bf = -1;}
else if (bf == -1)
{curleft->_bf = 0;cur->_bf = 1;parent->_bf = 0;
}
else
{assert(false);
}
}

新节点插入较高右子树的右侧

左单旋是指不平衡节点以及它的左子树进行旋转
同理，与插入到较高左子树的左侧对称，因此是左单旋

//新节点插入较高右子树的右侧----右右:左单旋
void RotateL(Node* parent)
{++_rotateCount;Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;/if (curleft){//parent->_right = curleft;curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}cur->_bf = parent->_bf = 0;
}

验证是否为平衡树

bool IsBlance()
{return IsBlance(_root);
}bool IsBlance(Node* root)
{if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << "平衡因子异常:" << root->_kv.first << " " << root->_bf << endl;return false;}return abs(rightHeight - leftHeight) < 2&& IsBlance(root->_right)&& IsBlance(root->_left);
}

二叉树的高度

int Height()
{return Height(_root);
}int Height(Node* root)
{if (root == nullptr){return 0;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

AVL的性能

AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度，即log_2 (N)。但是如果要对AVL树做一些结构修改的操作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。