作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263
邮箱 :291148484@163.com
本文地址:https://blog.csdn.net/qq_28550263/article/details/134474764
【简介】在3D计算机图形中,4x4矩阵最常见的用途是作为变换矩阵,这在各种 UI 框架中都非常常见,比如前端的 three.js 中也有类似对象。文本介绍 Flutter 中 Matrix4 矩阵变换的基础知识及其简单应用。本文涉及很一些学知识,不理解的读者可以参考线性代数相关教材。
目 录
- 1. 概述
- 2. 矩阵变换基础
- 2.1 矩阵的概念和性质
- 2.2 图形变换与 Matrix4 类
- 2.2.1 矩阵与变换
- 1. 旋转变换
- 2. 反射变换
- 3. 伸缩变换
- 4. 投影变换
- 5. 切变变换
- 5. 逆变换的概念
- 2.2.2 Matrix4 类
- 2.3 Flutter 中的坐标系统
- 3. Matrix4 的基本操作
- 4. 基于 Matrix4 的平移、缩放和旋转变换
- 5. 复合变换、逆变换和透视变换的实现
- 6. Matrix4 在动画和交互效果中的应用
1. 概述
在 Flutter 中,矩阵变换是一种强大的技术,它可以对目标对象进行各种变换,如缩放、平移和旋转。这种变换是通过使用 Matrix4,一个表示 4D 矩阵的类,来实现的。这里的 4D 并不是指四维空间,而是指这个矩阵有 4 行 4 列。通过改变这个矩阵的元素,我们可以实现对目标对象的各种变换。
Matrix4 的应用非常广泛,它可以用于各种图形和 3D 场景的变换。例如,我们可以通过改变矩阵的元素来控制图形的缩放比例、平移距离和旋转角度。这种变换方式的通用性使得我们可以在各种不同的场景中使用它。
矩阵变换是一种在 Flutter 中实现动画效果和交互效果的重要手段。通过理解和掌握 Matrix4 的使用,我们可以在 Flutter 中创建出各种各样的动画和交互效果。
2. 矩阵变换基础
2.1 矩阵的概念和性质
矩阵是一种特殊的数表,由 m 行 n 列的数值组成,通常用大写字母表示。矩阵的行数和列数称为矩阵的维度。矩阵的每个数值称为矩阵的元素。矩阵的加法、减法和乘法都有特定的运算规则。特别的,矩阵的乘法不满足交换律,即 AB ≠ BA。
2.2 图形变换与 Matrix4 类
2.2.1 矩阵与变换
要讲清楚矩阵和变换,就需要提一提线性代数中中的一些知识。同济六版线性代数教材中有一个很重要的应用就是“正交二次型”,其几何意义就是将一个图形变为对应的正交图形,就像用一个扳手将一个斜着或歪着的图形扳正——于是这个时候读了大学的你开始回忆,当年是如何求解将图形扳正的那个二次型的。但是实际上我们除了可以使用二次型将图形“扳正”,其实也可以通过变换将一个图形“扳”成其它样子,这就是线性变换的意义所在。
没有学过的也没事,我带大家过一遍。
1. 旋转变换
旋转变换是一种常见的线性变换,它可以将平面上的点或者空间中的点绕某一点旋转一定的角度。在二维平面上,一个点 (x, y) 绕原点旋转 θ 角度后的新坐标 (x’, y’) 可以通过以下矩阵乘法得到:

对应的旋转变换矩阵就是:

在三维空间中,绕 z 轴旋转的旋转变换矩阵为:

2. 反射变换
反射变换是一种将平面上的点或者空间中的点关于某条直线或者某个平面进行翻转的变换。
在二维平面上,关于 x 轴的反射变换矩阵为:

对应的变换矩阵为:

另外一种情况是,关于y=x轴变换,可以得到对应的变换矩阵为:

如果是三维空间中,关于 xy 平面的反射变换,对应矩阵为:

3. 伸缩变换
伸缩变换是一种将平面上的点或者空间中的点在某个方向上进行拉伸或者压缩的变换。在二维平面上,沿 x 轴方向进行伸缩的变换矩阵为:

4. 投影变换
投影变换是一种将空间中的点投影到某个平面上的变换。

在三维空间中,将点投影到 xy 平面上的投影变换矩阵为:

5. 切变变换
切变变换是一种将平面上的点或者空间中的点在某个方向上进行错切的变换。在二维平面上:
平行x轴的切边变换:

或者 平行y轴的切边变换:
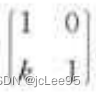
在三维空间中,沿 z 轴方向进行切变的变换矩阵为:

(其它轴类似)
要理解和运用矩阵变换,这些很重要。实际上后续小节的内容中,如果需要准确控制变换,没有这些数学知识是做不到的。其中,在后面的 4-3 小节中,有一个具体的例子,讲述了是如何应用到具体开发中的。
5. 逆变换的概念
逆变换是线性代数中的一个重要概念。对于一个线性变换,如果存在另一个线性变换,使得这两个变换的组合是恒等变换(即任何向量经过这两个变换后仍然保持不变),那么我们就说这两个变换是互逆的。
在矩阵表示的线性变换中,逆变换对应于矩阵的逆。给定一个矩阵 A,如果存在另一个矩阵 B,使得 AB = BA = E(其中 E 是单位矩阵),那么我们就说 B 是 A 的逆矩阵,记作
A^-1。
逆矩阵的存在性并不是总成立的,只有当矩阵是可逆的(或者说是非奇异的)时,逆矩阵才存在。在实际应用中,我们通常通过高斯消元法或者 LU 分解等方法来计算矩阵的逆。
逆变换在许多应用中都非常重要。例如,在解线性方程组时,我们可以通过求解系数矩阵的逆来找到解。在计算机图形学中,逆变换可以用来撤销之前的变换,或者从目标状态计算出初始状态。
从几何意义上说,逆矩阵对应的是逆变换。一个变换让图形产生某个形变,那么一个对应的逆变换让变换后的图形还原原来的样子。
2.2.2 Matrix4 类
在 3D 图形的变换中,我们通常使用 4x4 的矩阵,这种矩阵可以表示平移、缩放、旋转等变换,也可以表示这些变换的组合。在这个矩阵中,最后一列通常用于表示平移变换,其余部分用于表示缩放和旋转变换。
在 Flutter 中,这种 4x4 矩阵由 Matrix4 类来表示。Matrix4 类提供了一系列的方法,可以方便地创建和操作 4x4 矩阵实现 3D图形变换。例如:
- Matrix4.identity() 可以创建一个单位矩阵;
- Matrix4.diagonal3Values() 可以创建一个对角矩阵;
- Matrix4.compose() 可以创建一个表示组合变换的矩阵。
2.3 Flutter 中的坐标系统
对于手机屏幕来讲,坐标系的:
- 原点 在手机屏幕的左上角;
- 水平向右是 x 轴的正方向;
- 竖直向下是 y 轴的正方向;
- 垂直于屏幕的方向是 z 轴。
这种坐标系统的设计使得我们可以方便地定位屏幕上的任何一个点,也方便我们使用 Matrix4 进行图形的变换。
3. Matrix4 的基本操作
3.1 创建 Matrix4 对象
在 Flutter 中,我们可以使用多种方式创建 Matrix4 对象。最简单的方式是使用 Matrix4 的构造函数,这将创建一个全零的矩阵。如果我们想创建一个单位矩阵,可以使用 Matrix4.identity() 方法。此外,我们还可以使用 Matrix4.diagonal3Values() 方法创建一个对角矩阵,或者使用 Matrix4.compose() 方法创建一个表示组合变换的矩阵。
Matrix4 matrix1 = Matrix4(); // 创建一个全零的矩阵
Matrix4 matrix2 = Matrix4.identity(); // 创建一个单位矩阵
Matrix4 matrix3 = Matrix4.diagonal3Values(1.0, 2.0, 3.0); // 创建一个对角矩阵
矩阵的本质是变换,在上面几个矩阵的示例中,代表了不同的变换:
- Matrix4 matrix1 = Matrix4(); 创建的是一个全零矩阵。在大多数情况下,全零矩阵在图形变换中没有实际用途,因为它会将所有的点都映射到原点;
- Matrix4 matrix2 = Matrix4.identity(); 创建的是一个单位矩阵。单位矩阵在变换中相当于“无操作”,因为任何向量与单位矩阵相乘都会得到原向量。它常用作变换矩阵的初始值,然后通过应用一系列的变换(如旋转、缩放等)来修改这个矩阵;
- Matrix4 matrix3 = Matrix4.diagonal3Values(1.0, 2.0, 3.0); 创建的是一个对角矩阵。对角矩阵可以用来进行均匀或非均匀的缩放。例如,上述代码创建的矩阵会在 x 轴方向上保持原大小,在 y 轴方向上放大 2 倍,在 z 轴方向上放大 3 倍。
3.2 Matrix4 的基本方法
Matrix4 类提供了一系列的基本方法,可以用于获取和设置矩阵的元素,以及进行矩阵的基本运算。例如,我们可以使用 [] 运算符获取和设置矩阵的元素,使用 + 和 - 运算符进行矩阵的加法和减法运算,使用 运算符进行矩阵的乘法运算。
double value = matrix1[0]; // 获取矩阵的元素
matrix1[0] = value; // 设置矩阵的元素
Matrix4 result1 = matrix1 + matrix2; // 矩阵的加法运算
Matrix4 result2 = matrix1 - matrix2; // 矩阵的减法运算
Matrix4 result3 = matrix1 * matrix2; // 矩阵的乘法运算
3.3 Matrix4 的变换方法
Matrix4 类提供了一系列的变换方法,可以用于对矩阵进行平移、缩放、旋转等变换。这些方法都会改变矩阵的元素,从而实现对目标对象的变换。
matrix1.translate(10.0, 20.0, 30.0); // 平移变换
matrix1.scale(2.0, 3.0, 4.0); // 缩放变换
matrix1.rotateX(1.0); // 绕 x 轴旋转
matrix1.rotateY(1.0); // 绕 y 轴旋转
matrix1.rotateZ(1.0); // 绕 z 轴旋转
4. 基于 Matrix4 的平移、缩放和旋转变换
4.1 使用 Matrix4 进行平移变换
在 Flutter 中,我们可以使用 Matrix4 的 translate 方法进行平移变换。这个方法接受三个参数,分别表示在 x、y 和 z 轴上的平移距离。
Matrix4 matrix = Matrix4.identity();
matrix.translate(10.0, 20.0, 30.0); // 在 x、y 和 z 轴上分别平移 10、20 和 30 单位
这将会改变 Matrix4 对象的元素,使得它表示一个平移变换。我们可以将这个矩阵应用到一个图形上,使得这个图形在 x、y 和 z 轴上分别平移 10、20 和 30 单位。
4.2 使用 Matrix4 进行缩放变换
我们可以使用 Matrix4 的 scale 方法进行缩放变换。这个方法接受三个参数,分别表示在 x、y 和 z 轴上的缩放比例。
Matrix4 matrix = Matrix4.identity();matrix.scale(2.0, 3.0, 4.0); // 在 x、y 和 z 轴上分别缩放 2、3 和 4 倍
这将会改变 Matrix4 对象的元素,使得它表示一个缩放变换。我们可以将这个矩阵应用到一个图形上,使得这个图形在 x、y 和 z 轴上分别缩放 2、3 和 4 倍。
4.3 使用 Matrix4 进行旋转变换
Matrix4 类提供了 rotateX、rotateY 和 rotateZ 三个方法,可以用于进行旋转变换。这些方法接受一个参数,表示旋转的角度。
Matrix4 matrix = Matrix4.identity();matrix.rotateX(1.0); // 绕 x 轴旋转 1 弧度matrix.rotateY(1.0); // 绕 y 轴旋转 1 弧度matrix.rotateZ(1.0); // 绕 z 轴旋转 1 弧度
这将会改变 Matrix4 对象的元素,使得它表示一个旋转变换。我们可以将这个矩阵应用到一个图形上,使得这个图形分别绕 x、y 和 z 轴旋转 1 弧度。
实际上,要准确控制,还是要回到之前的数学知识。结合之前讲解的代数学知识,以绕x轴旋转为例。当绕x轴旋转时,旋转矩阵为:
[ 1 0 0 0 cos θ − sin θ 0 sin θ cos θ ] \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{bmatrix} 1000cosθsinθ0−sinθcosθ
对应的用于 Matrix4 的矩阵表示为:
[ 1 0 0 0 0 cos θ − sin θ 0 0 sin θ cos θ 0 0 0 0 1 ] \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta & 0 \\ 0 & \sin\theta & \cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} 10000cosθsinθ00−sinθcosθ00001
在这个基础上,以绕x轴正向旋转为例:
-
首先,我们需要创建一个 Matrix4 实例。
-
然后,我们可以使用 Matrix4 的 setEntry 方法来设置矩阵的元素。对于绕 x 轴旋转的变换,我们需要设置的元素如下:
- 第二行第二列的元素为 cosθ
- 第二行第三列的元素为 -sinθ
- 第三行第二列的元素为 sinθ
- 第三行第三列的元素为 cosθ
- 最后,我们可以使用这个 Matrix4 实例来对图形进行变换。
// 创建一个 Matrix4 实例
final matrix4 = Matrix4.identity();// 设置旋转角度
final theta = math.pi / 4; // 旋转 45 度// 设置矩阵的元素
matrix4.setEntry(1, 1, math.cos(theta));
matrix4.setEntry(1, 2, -math.sin(theta));
matrix4.setEntry(2, 1, math.sin(theta));
matrix4.setEntry(2, 2, math.cos(theta));// 使用 Matrix4 实例来对图形进行变换
final transformedWidget = Transform(transform: matrix4,child: /* 变换的组件 */,
);
上面的代码中,我们首先创建了一个 Matrix4 实例,然后设置了旋转角度为 45 度,接着设置了矩阵的元素,最后使用这个 Matrix4 实例来对图形进行变换。
在实际应用中,我们通常会先定义一个变换矩阵来表示变换,然后再将其应用到图形上。在 Flutter 中,我们可以使用 Matrix4 的构造函数来直接创建一个表示特定变换的矩阵。
比如:
import 'dart:math' as math;
import 'package:flutter/widgets.dart';// 设置旋转角度
final theta = math.pi / 4; // 旋转 45 度// 定义一个表示旋转变换的矩阵
final matrix4 = Matrix4(1, 0, 0, 0,0, math.cos(theta), -math.sin(theta), 0,0, math.sin(theta), math.cos(theta), 0,0, 0, 0, 1,
);// 将 Matrix4 转换为 List<double>
final matrix4List = matrix4.storage.toList();// 使用 Matrix4 实例来对图形进行变换
final transformedWidget = Transform(transform: matrix4,child: /* your widget */,
);
旋转45度是一个特例,我们可以在理解的基础上进一步写成一个函数,用于绕 x 轴旋转,就像这样:
import 'dart:math' as math;Matrix4 rotationMatrix(double angleInDegrees) {// 将角度转换为弧度final theta = angleInDegrees / 180.0 * math.pi;// 创建一个列表来表示矩阵final matrix = [[1, 0, 0, 0],[0, math.cos(theta), -math.sin(theta), 0],[0, math.sin(theta), math.cos(theta), 0],[0, 0, 0, 1],];// 创建一个 Matrix4 实例final matrix4 = Matrix4.fromList(matrix.expand((i) => i).toList());return matrix4;
}
这个函数中,我们首先将输入的角度转换为弧度,然后创建了一个列表来表示矩阵,最后将这个列表转换为 Matrix4 实例并返回。这样,我们就可以通过调用这个函数来创建任意角度的绕 x 轴旋转矩阵了。这个列表 matrix ,就表示的是绕 x 轴旋转变换所用的变换矩阵。
仅举这个例子作为示范,其它的情况都是之前提到数学知识的应用,读者可以按照这个思路参考得出。
5. 复合变换、逆变换和透视变换的实现
5.1 使用 Matrix4 进行复合变换
在 Flutter 中,我们可以通过连续调用 Matrix4 的变换方法来实现复合变换。例如,我们可以先进行平移变换,然后进行缩放变换,最后进行旋转变换。
Matrix4 matrix = Matrix4.identity();
matrix.translate(10.0, 20.0, 30.0); // 平移变换
matrix.scale(2.0, 3.0, 4.0); // 缩放变换
matrix.rotateZ(1.0); // 旋转变换
这将会改变 Matrix4 对象的元素,使得它表示一个复合变换。我们可以将这个矩阵应用到一个图形上,使得这个图形先进行平移变换,然后进行缩放变换,最后进行旋转变换。
5.2 使用 Matrix4 进行逆变换
Matrix4 类提供了 invert 方法,可以用于计算矩阵的逆。逆变换可以用于撤销之前的变换。
Matrix4 matrix = Matrix4.identity();matrix.translate(10.0, 20.0, 30.0); // 平移变换Matrix4 inverseMatrix = Matrix4.inverted(matrix); // 计算逆变换
这将会创建一个新的 Matrix4 对象,它表示的变换可以撤销原来的变换。我们可以将这个矩阵应用到一个图形上,使得这个图形恢复到原来的状态。
5.3 使用 Matrix4 进行透视变换
Matrix4 类提供了 setEntry 方法,可以用于设置矩阵的元素。我们可以通过设置矩阵的元素来实现透视变换。
Matrix4 matrix = Matrix4.identity();
matrix.setEntry(3, 2, 0.001); // 设置矩阵的元素,实现透视变换
这将会改变 Matrix4 对象的元素,使得它表示一个透视变换。我们可以将这个矩阵应用到一个图形上,使得这个图形产生透视效果。
6. Matrix4 在动画和交互效果中的应用
6.1 使用 Matrix4 创建动画效果
在 Flutter 中,我们可以使用 Matrix4 和动画控制器(AnimationController)一起创建动画效果。例如,我们可以创建一个动画,使得一个图形在一段时间内进行平移、缩放和旋转变换。
AnimationController controller = AnimationController(duration: const Duration(seconds: 2),vsync: this,);Matrix4 matrix = Matrix4.identity();controller.addListener(() {matrix.translate(controller.value * 10.0, controller.value * 20.0, controller.value * 30.0);matrix.scale(controller.value * 2.0, controller.value * 3.0, controller.value * 4.0);matrix.rotateZ(controller.value * 1.0);});controller.forward();
这将会创建一个动画,使得一个图形在 2 秒内进行平移、缩放和旋转变换。
6.2 使用 Matrix4 创建交互效果
我们可以使用 Matrix4 和手势识别器(GestureRecognizer)一起创建交互效果。例如,我们可以创建一个交互效果,使得用户可以通过拖动来控制一个图形的平移变换。
Matrix4 matrix = Matrix4.identity();double dx = 0.0, dy = 0.0;GestureDetector(onPanUpdate: (details) {dx += details.delta.dx;dy += details.delta.dy;matrix.setIdentity();matrix.translate(dx, dy);},child: Transform(transform: matrix,child: FlutterLogo(size: 100.0),),);
这将会创建一个交互效果,使得用户可以通过拖动来控制一个图形的平移变换。
6.3 使用 Matrix4 创建 3D 效果
我们可以使用 Matrix4 创建 3D 效果。例如,我们可以创建一个效果,使得一个图形在 3D 空间中进行旋转。
Matrix4 matrix = Matrix4.identity();matrix.setEntry(3, 2, 0.001); // 设置矩阵的元素,实现透视效果matrix.rotateY(1.0); // 绕 y 轴旋转Transform(transform: matrix,child: FlutterLogo(size: 100.0),);
这将会创建一个 3D 效果,使得一个图形在 3D 空间中进行旋转。




![集成多元算法,打造高效字面文本相似度计算与匹配搜索解决方案,助力文本匹配冷启动[BM25、词向量、SimHash、Tfidf、SequenceMatcher]](https://img-blog.csdnimg.cn/d553c7dadca54bdb82a3a234befb74d8.png#pic_center)