VAE模型及pytorch实现
- VAE模型推导部分
- 最小化KL散度推导
- 代码部分
- 损失函数
- Encoder部分
- Decoder部分
- VAE整体架构
- VAE问题
- 参考资料
VAE(变分自编码器)是一种生成模型,结合了自编码器和概率图模型的思想。它通过学习数据的潜在分布,可以生成新的数据样本。VAE通过将输入数据映射到潜在空间中的分布,并在训练过程中最大化数据与潜在变量之间的条件概率来实现。其关键思想在于编码器将输入数据编码成潜在分布的参数,解码器则从这个分布中采样生成新的数据。这种生成方式不仅能够生成新的数据,还能够在潜在空间中进行插值和操作,提供了强大的特征学习和数据生成能力。
AE论文:Auto-Encoding Variational Bayes
VAE论文:Semi-supervised Learning with Deep Generative Models
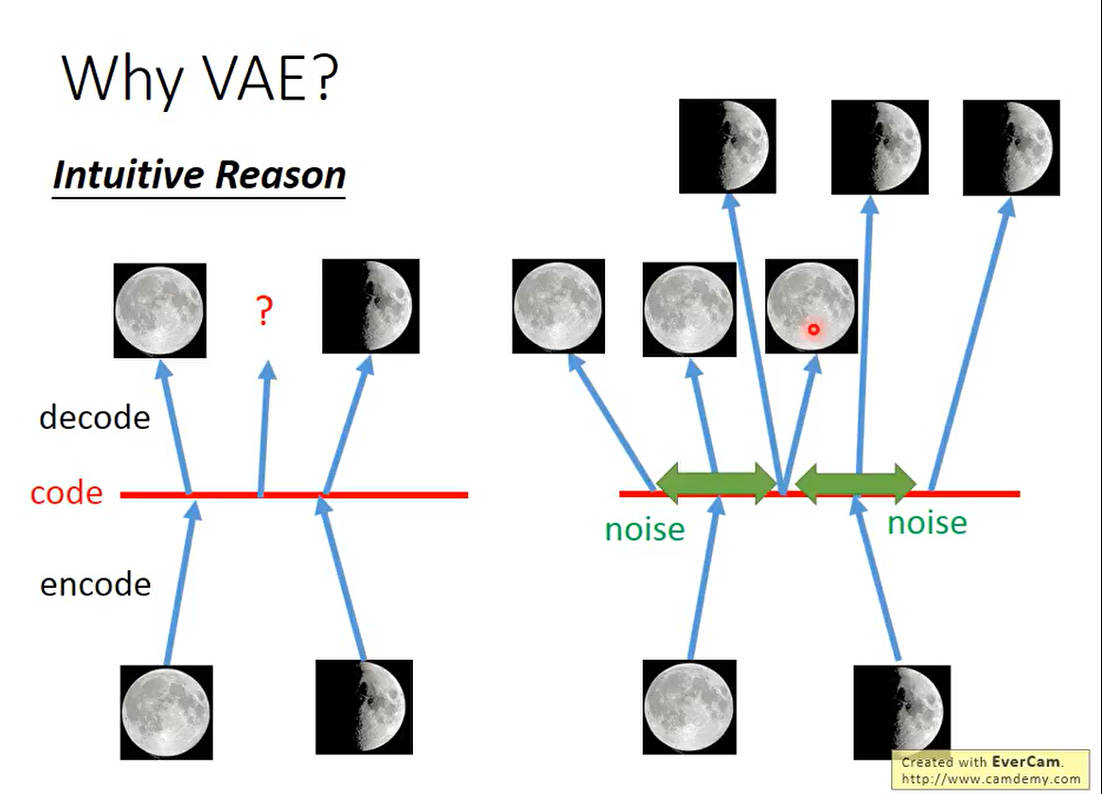
VAE模型推导部分

假设 P ( z ) P(z) P(z)是一个正态分布, x ∣ z ∼ N ( μ ( z ) , σ ( z ) ) x|z \sim N(\mu(z),\sigma(z)) x∣z∼N(μ(z),σ(z))是x从z分布中进行采样得到的。
P ( x ) = ∫ z P ( z ) P ( x ∣ z ) d z P(x)=\int_zP(z)P(x|z)dz P(x)=∫zP(z)P(x∣z)dz
为了最大化 P ( x ) P(x) P(x),我们采用极大似然估计
L = ∑ x l o g P ( x ) M a x i m i z i n g t h e l i k e l i h o o d o f t h e o b s e r v e d x L=\sum_{x}logP(x)\quad\mathrm{Maximizing~the~likelihood~of~the~observed~x} L=x∑logP(x)Maximizing the likelihood of the observed x
对 l o g P ( x ) logP(x) logP(x)进一步进行变形
l o g P ( x ) = ∫ z q ( z ∣ x ) l o g P ( x ) d z q ( z ∣ x ) c a n b e a n y d i s t r i b u t i o n = ∫ z q ( z ∣ x ) l o g ( P ( z , x ) P ( z ∣ x ) ) d z = ∫ z q ( z ∣ x ) l o g ( P ( z , x ) q ( z ∣ x ) q ( z ∣ x ) P ( z ∣ x ) ) d z = ∫ z q ( z ∣ x ) l o g ( P ( z , x ) q ( z ∣ x ) ) d z + ∫ z q ( z ∣ x ) l o g ( q ( z ∣ x ) P ( z ∣ x ) ) d z ≥ ∫ z q ( z ∣ x ) l o g ( P ( x ∣ z ) P ( z ) q ( z ∣ x ) ) d z \begin{aligned} logP(x)=&\int_{z}q(z|x)logP(x)dz\quad\mathrm{q(z|x)~can~be~any~distribution} \\ &=\int_{z}q(z|x)log\left(\frac{P(z,x)}{P(z|x)}\right)dz=\int_{z}q(z|x)log\left(\frac{P(z,x)}{q(z|x)}\frac{q(z|x)}{P(z|x)}\right)dz \\ &=\int_{z}q(z|x)log\left(\frac{P(z,x)}{q(z|x)}\right)dz+\int_{z}q(z|x)log\left(\frac{q(z|x)}{P(z|x)}\right)dz \\ &\geq \int_{z}q(z|x)log\left(\frac{P(x|z)P(z)}{q(z|x)}\right)dz \end{aligned} logP(x)=∫zq(z∣x)logP(x)dzq(z∣x) can be any distribution=∫zq(z∣x)log(P(z∣x)P(z,x))dz=∫zq(z∣x)log(q(z∣x)P(z,x)P(z∣x)q(z∣x))dz=∫zq(z∣x)log(q(z∣x)P(z,x))dz+∫zq(z∣x)log(P(z∣x)q(z∣x))dz≥∫zq(z∣x)log(q(z∣x)P(x∣z)P(z))dz
因为 K L ( q ( z ∣ x ) ∣ ∣ P ( z ∣ x ) ) = ∫ z q ( z ∣ x ) l o g ( q ( z ∣ x ) P ( z ∣ x ) ) d z KL\left(q(z|x)||P(z|x)\right)=\int_{z}q(z|x)log\left(\frac{q(z|x)}{P(z|x)}\right)dz KL(q(z∣x)∣∣P(z∣x))=∫zq(z∣x)log(P(z∣x)q(z∣x))dz是大于0的数,所以,上述式子大于等于前面那一项。
对于给定的 P ( x ∣ z ) P(x|z) P(x∣z),让KL尽可能小,就是让 L b L_b Lb最大。同时,当 K L KL KL尽可能小,也就是说明 q ( z ∣ x ) q(z|x) q(z∣x)和 p ( z ∣ x ) p(z|x) p(z∣x)这两个分布的相似度越高。
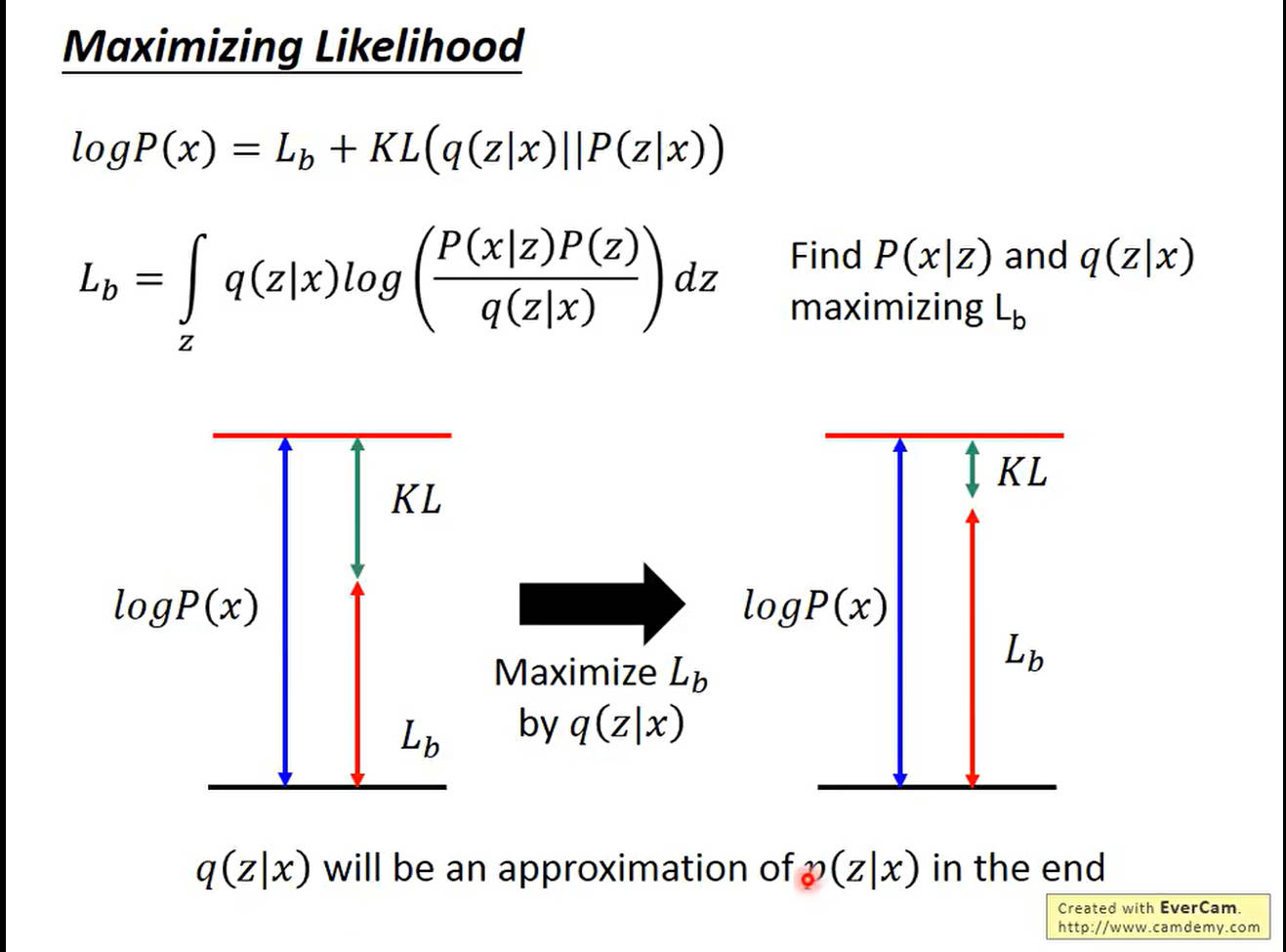
接下来我们就对 L b L_b Lb进行最大化变形处理,变形后左侧为,右侧为
L b = ∫ z q ( z ∣ x ) l o g ( P ( z , x ) q ( z ∣ x ) ) d z = ∫ z q ( z ∣ x ) l o g ( P ( x ∣ z ) P ( z ) q ( z ∣ x ) ) d z = ∫ z q ( z ∣ x ) log ( P ( z ) q ( z ∣ x ) ) d z + ∫ z q ( z ∣ x ) l o g P ( x ∣ z ) d z = K L ( q ( z ∣ x ) ∣ ∣ P ( z ) ) + E q ( z ∣ x ) [ l o g P ( x ∣ z ) ] \begin{aligned} L_b&=\int_zq(z|x)log\left(\frac{P(z,x)}{q(z|x)}\right)dz=\int_zq(z|x)log\left(\frac{P(x|z)P(z)}{q(z|x)}\right)dz\\ &=\int_z q(z|x)\log (\frac{P(z)}{q(z|x)})dz+\int_zq(z|x)logP(x|z)dz\\ &=KL(q(z|x)||P(z))+E_{q(z|x)}[logP(x|z)] \end{aligned} Lb=∫zq(z∣x)log(q(z∣x)P(z,x))dz=∫zq(z∣x)log(q(z∣x)P(x∣z)P(z))dz=∫zq(z∣x)log(q(z∣x)P(z))dz+∫zq(z∣x)logP(x∣z)dz=KL(q(z∣x)∣∣P(z))+Eq(z∣x)[logP(x∣z)]
如下所示,我们需要做的就是最小化 K L ( q ( z ∣ x ) ∣ ∣ P ( z ) ) KL(q(z|x)||P(z)) KL(q(z∣x)∣∣P(z))并最大化 E q ( z ∣ x ) [ l o g P ( x ∣ z ) ] E_{q(z|x)}[logP(x|z)] Eq(z∣x)[logP(x∣z)]。对于最小化KL,我们可以理解为输入一个 x x x,然后通过神经网络调参输出 μ ( x ) , σ ( x ) \mu_(x),\sigma(x) μ(x),σ(x),也就是让这个数值尽可能和 P ( z ) P(z) P(z)这个分布接近。这部分相当于Encoder部分。
在Encoder部分结束后,对于第2项,从已知的 z z z,也就是数据的隐式特征表示,去采样出 x x x,相当于模型的Decoder部分,输出一个均值使之尽可能接近原始的 x x x,因为对于这种条件概率,均值最大的时候就是 x x x
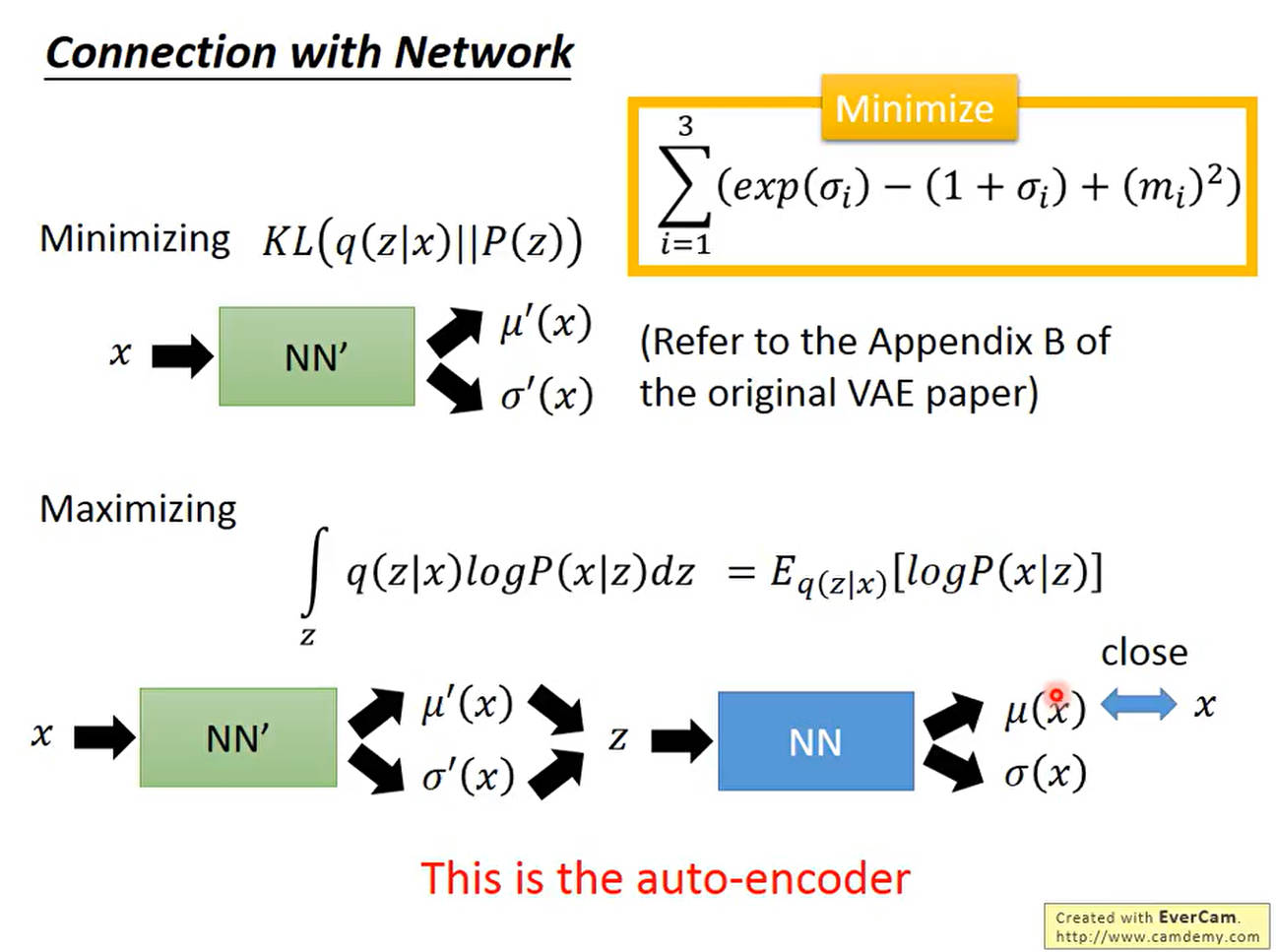
最小化KL散度推导
为了最小化 q ( z ∣ x ) q(z|x) q(z∣x)和 P ( z ) P(z) P(z)的KL散度,首先,我们先对正态分布的KL散度计算进行推导。参考链接高斯分布的KL散度-CSDN博客
K L ( N ( μ 1 , σ 1 2 ) ∥ N ( μ 2 , σ 2 2 ) ) = ∫ x 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 log 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 1 2 π σ 2 e − ( x − μ 2 ) 2 2 σ 2 2 d x = ∫ x 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 [ log σ 2 σ 1 − ( x − μ 1 ) 2 2 σ 1 2 + ( x − μ 2 ) 2 2 σ 2 2 ] d x \begin{aligned} \mathrm{KL}\left(\mathcal{N}\left(\mu_{1}, \sigma_{1}^{2}\right) \| \mathcal{N}\left(\mu_{2}, \sigma_{2}^{2}\right)\right) & =\int_{\mathrm{x}} \frac{1}{\sqrt{2 \pi} \sigma_{1}} \mathrm{e}^{-\frac{\left(x-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}} \log \frac{\frac{1}{\sqrt{2 \pi} \sigma_{1}} e^{-\frac{\left(x-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}}}{\frac{1}{\sqrt{2 \pi} \sigma_{2}} e^{-\frac{\left(x-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}}} d x \\ & =\int_{x} \frac{1}{\sqrt{2 \pi} \sigma_{1}} e^{-\frac{\left(x-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}}\left[\log \frac{\sigma_{2}}{\sigma_{1}}-\frac{\left(x-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}+\frac{\left(x-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}\right] d x \end{aligned}\\ KL(N(μ1,σ12)∥N(μ2,σ22))=∫x2πσ11e−2σ12(x−μ1)2log2πσ21e−2σ22(x−μ2)22πσ11e−2σ12(x−μ1)2dx=∫x2πσ11e−2σ12(x−μ1)2[logσ1σ2−2σ12(x−μ1)2+2σ22(x−μ2)2]dx
-
对于第1项,由于 σ 1 , σ 2 \sigma_1,\sigma_2 σ1,σ2与x无关,则可以直接提取到积分外面,该积分即为正态分布的全概率公式,也就是为1
log σ 2 σ 1 ∫ x 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 d x = log σ 2 σ 1 \log \frac{\sigma_{2}}{\sigma_{1}} \int_{\mathrm{x}} \frac{1}{\sqrt{2 \pi} \sigma_{1}} \mathrm{e}^{-\frac{\left(x-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}} \mathrm{dx}=\log \frac{\sigma_{2}}{\sigma_{1}}\\ logσ1σ2∫x2πσ11e−2σ12(x−μ1)2dx=logσ1σ2 -
对于第2项,则是由方差定义式 D ( x ) = ∫ x ( x − μ ) 2 f ( x ) d x D(x)=\int_x(x-\mu)^2f(x)dx D(x)=∫x(x−μ)2f(x)dx,可知这个积分的结果为 σ 1 2 \sigma_1^2 σ12
− 1 2 σ 1 2 ∫ x ( x − μ 1 ) 2 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 d x = − 1 2 σ 1 2 σ 1 2 = − 1 2 -\frac{1}{2 \sigma_{1}^{2}} \int_{\mathrm{x}}\left(\mathrm{x}-\mu_{1}\right)^{2} \frac{1}{\sqrt{2 \pi} \sigma_{1}} \mathrm{e}^{-\frac{\left(\mathrm{x}-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}} \mathrm{dx}=-\frac{1}{2 \sigma_{1}^{2}} \sigma_{1}^{2}=-\frac{1}{2} −2σ121∫x(x−μ1)22πσ11e−2σ12(x−μ1)2dx=−2σ121σ12=−21 -
对于第3项,首先将其展开,对于 x 2 x^2 x2,由均方值公式, E ( x 2 ) = D ( x ) + E ( x ) 2 E(x^2)=D(x)+E(x)^2 E(x2)=D(x)+E(x)2,后面两项则分别是通过均值公式以及全概率公式进行计算。
1 2 σ 2 2 ∫ x ( x − μ 2 ) 2 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 d x = 1 2 σ 2 2 ∫ x ( x 2 − 2 μ 2 x + μ 2 2 ) 1 2 π σ 1 e − ( x − μ 1 ) 2 2 σ 1 2 d x = σ 1 2 + μ 1 2 − 2 μ 1 μ 2 + μ 2 2 2 σ 2 2 = σ 1 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 \begin{aligned} \frac{1}{2 \sigma_{2}^{2}} \int_{\mathrm{x}}\left(\mathrm{x}-\mu_{2}\right)^{2} \frac{1}{\sqrt{2 \pi} \sigma_{1}} \mathrm{e}^{-\frac{\left(\mathrm{x}-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}} \mathrm{dx} & =\frac{1}{2 \sigma_{2}^{2}} \int_{\mathrm{x}}\left(\mathrm{x}^{2}-2 \mu_{2} \mathrm{x}+\mu_{2}^{2}\right) \frac{1}{\sqrt{2 \pi} \sigma_{1}} \mathrm{e}^{-\frac{\left(\mathrm{x}-\mu_{1}\right)^{2}}{2 \sigma_{1}^{2}}} \mathrm{dx} \\ & =\frac{\sigma_{1}^{2}+\mu_{1}^{2}-2 \mu_{1} \mu_{2}+\mu_{2}^{2}}{2 \sigma_{2}^{2}}=\frac{\sigma_{1}^{2}+\left(\mu_{1}-\mu_{2}\right)^{2}}{2 \sigma_{2}^{2}}\\ \end{aligned} 2σ221∫x(x−μ2)22πσ11e−2σ12(x−μ1)2dx=2σ221∫x(x2−2μ2x+μ22)2πσ11e−2σ12(x−μ1)2dx=2σ22σ12+μ12−2μ1μ2+μ22=2σ22σ12+(μ1−μ2)2
对上述式子进行汇总:
K L ( N ( μ 1 , σ 1 2 ) ∥ N ( μ 2 , σ 2 2 ) ) = log σ 2 σ 1 − 1 2 + σ 1 2 + ( μ 1 − μ 2 ) 2 2 σ 2 2 = 1 2 ( σ 1 2 + μ 1 2 − log σ 1 2 − 1 ) \begin{aligned} \mathrm{KL}\left(\mathcal{N}\left(\mu_{1}, \sigma_{1}^{2}\right) \| \mathcal{N}\left(\mu_{2}, \sigma_{2}^{2}\right)\right) &=\log{\frac{\sigma_2}{\sigma_1}-\frac{1}{2}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}} \\&=\frac{1}{2}(\sigma_1^2+\mu_1^2-\log^{\sigma_1^2}-1) \end{aligned} KL(N(μ1,σ12)∥N(μ2,σ22))=logσ1σ2−21+2σ22σ12+(μ1−μ2)2=21(σ12+μ12−logσ12−1)
代码部分
损失函数
通过上述推导,我们知道了需要最小化散度,然后最大化那个均值。所以可以得到如下的损失函数。
def loss_fn(recon_x, x, mean, log_var):BCE = torch.nn.functional.binary_cross_entropy(recon_x.view(-1, 28*28), x.view(-1, 28*28), reduction='sum')KLD = -0.5 * torch.sum(1 + log_var - mean.pow(2) - log_var.exp())return (BCE + KLD) / x.size(0)
Encoder部分
class Encoder(nn.Module):def __init__(self, layer_sizes, latent_size):super(Encoder, self).__init__()self.MLP = nn.Sequential()for i, (in_size, out_size) in enumerate(zip(layer_sizes[:-1], layer_sizes[1:])):self.MLP.add_module(name="L{:d}".format(i), module=nn.Linear(in_size, out_size))self.MLP.add_module(name="A{:d}".format(i), module=nn.ReLU())# 首先对图像特征进行一些变换处理,然后将其展开成一维向量,然后通过全连接层得到均值和方差self.linear_means = nn.Linear(layer_sizes[-1], latent_size)self.linear_log_var = nn.Linear(layer_sizes[-1], latent_size)def forward(self, x):x = self.MLP(x)means = self.linear_means(x)log_vars = self.linear_log_var(x)return means, log_vars
Decoder部分
class Decoder(nn.Module):def __init__(self, layer_sizes, latent_size):super(Decoder, self).__init__()self.MLP = nn.Sequential()input_size = latent_sizefor i, (in_size, out_size) in enumerate(zip([input_size] + layer_sizes[:-1], layer_sizes)):self.MLP.add_module(name="L{:d}".format(i), module=nn.Linear(in_size, out_size))if i + 1 < len(layer_sizes):self.MLP.add_module(name="A{:d}".format(i), module=nn.ReLU())else:self.MLP.add_module(name="sigmoid", module=nn.Sigmoid())def forward(self, z):#对输入的z进行全接连操作,最后输出一个重构的xx = self.MLP(z)return x
VAE整体架构
class VAE(nn.Module):def __init__(self, encoder_layer_sizes, latent_size, decoder_layer_sizes):super(VAE, self).__init__()self.latent_size = latent_sizeself.encoder = Encoder(encoder_layer_sizes, latent_size)self.decoder = Decoder(decoder_layer_sizes, latent_size)def forward(self, x):if x.dim() > 2:x = x.view(-1, 28 * 28)means, log_var = self.encoder(x)z = self.reparameterize(means, log_var)recon_x = self.decoder(z)return recon_x, means, log_var, zdef reparameterize(self, mu, log_var):"""用于对encoder部分输出的均值方差进行重参数化,采样得到隐式表示部分z:param mu::param log_var::return:"""std = torch.exp(0.5 * log_var)eps = torch.randn_like(std)return mu + eps * stddef inference(self, z):recon_x = self.decoder(z)return recon_x
VAE问题
vae只是记住图片,而不是生成图片
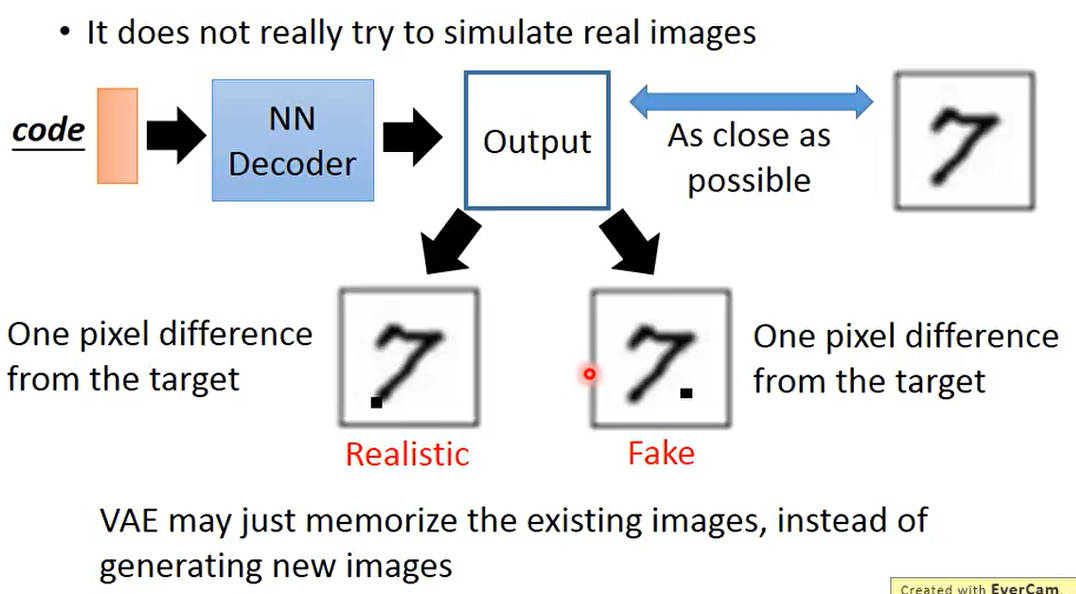
再产生图片时,只是通过像素差异进行评估,则对于关键点像素和可忽略像素之间的图片,两者在vae看来是一致的,但是不是理想的产生图片,因此出现了GAN
参考资料
VAE 模型基本原理简单介绍_vae模型-CSDN博客
高斯分布的KL散度-CSDN博客
ML Lecture 18: Unsupervised Learning - Deep Generative Model (Part II)