一、前言
ChatGPT GPT4.0,Midjourney绘画,相信对大家应该不感到陌生吧?简单来说,GPT-4技术比之前的GPT-3.5相对来说更加智能,会根据用户的要求生成多种内容甚至也可以和用户进行创作交流。 然而,GPT-4对普通用户来说都是需要额外付费才可以使用。所以今天小编就整理一个真正免费的AI工具。不是一天只能使用一两次就不能使用的网站。
我们也忍不住做了一个基于ChatGPT的网站,可以免登陆!!国内可直接对话AI,也有各种提供工作效率的工具供大家使用。

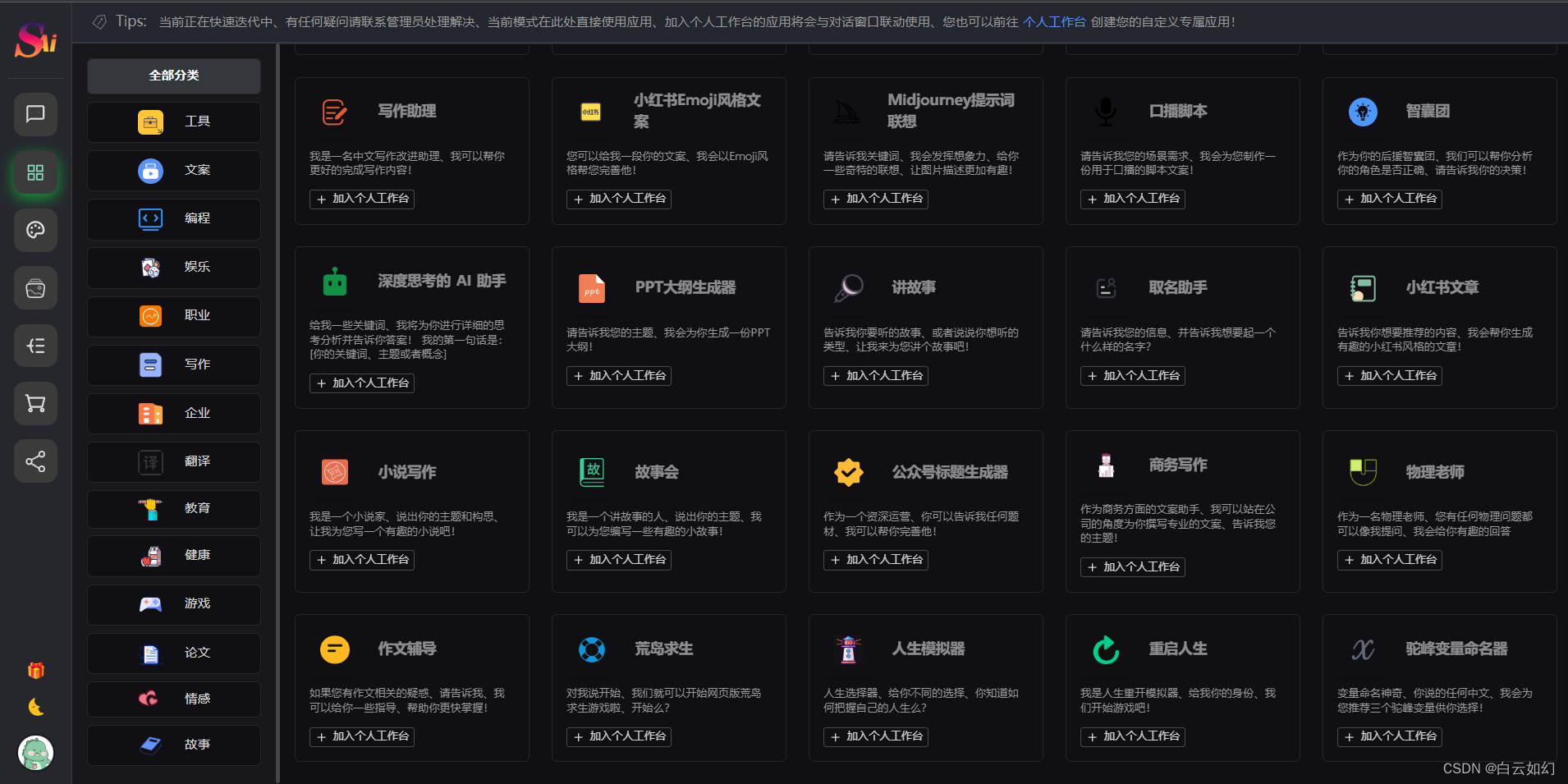
二、特点优势
- 该网站无需魔法,国内直接使用
- 该网站长期运营,为国内博主自己掏腰包免费给粉丝使用
- 支持手机端
- 支持GPT-4-Turbo模型
- 支持DALL-E3文生图
- 支持最新GPT-4-Turbo模型、GPT-4-1106-Preview多模态模型
- 支持GPT-4图片对话能力上传图片并识图理解对话
- 其他功能持续迭代更新中...
三、上干货
AI网址:
https://ai.sparkaigf.com
系统详细文档:
https://www.yuque.com/yuqueyonghutq9yt2/egy0d0/ah9sq89lgl6b7s4w
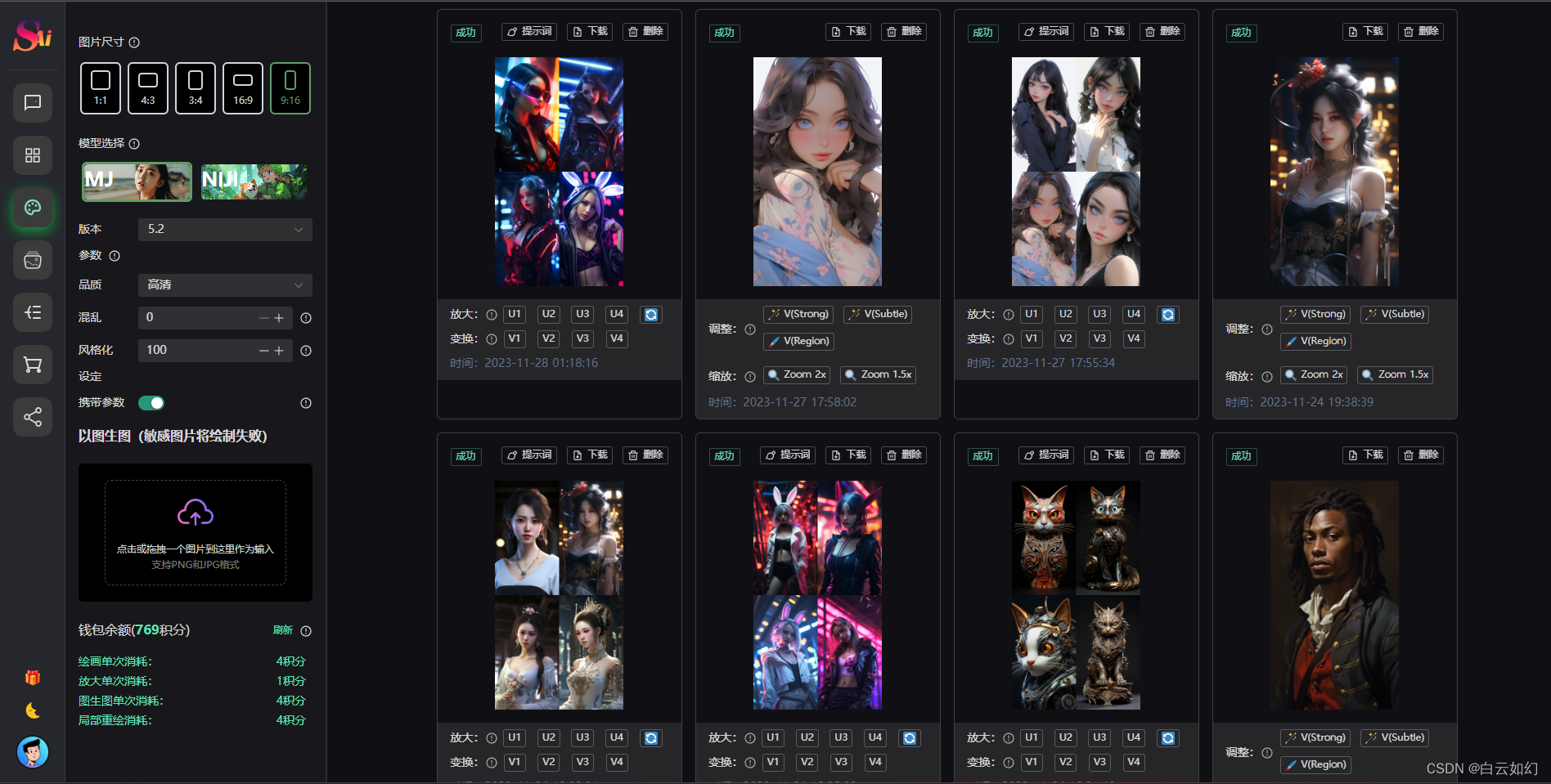
四、支持Midjourney绘画
使用AI即可轻松完成绘画。
- 支持同步官方图片重新生成指令
- 同步官方 Vary 指令 单张图片对比加强 Vary(Strong) | Vary(Subtle)
- 同步官方 Zoom 指令 单张图片无限缩放 Zoom out 2x | Zoom out 1.5x
- 新增 Midjourney局部重绘(Vary Region)在线编辑功能

本系统使用Nestjs+Vue+Typescript框架技术,持续集成AI能力到本系统。支持GPT-4-Turbo模型、支持DALL-E3文生图,支持最新GPT-4-Turbo模型、GPT-4-1106-Preview多模态模型。支持GPT-4图片对话能力上传图片并识图理解对话。