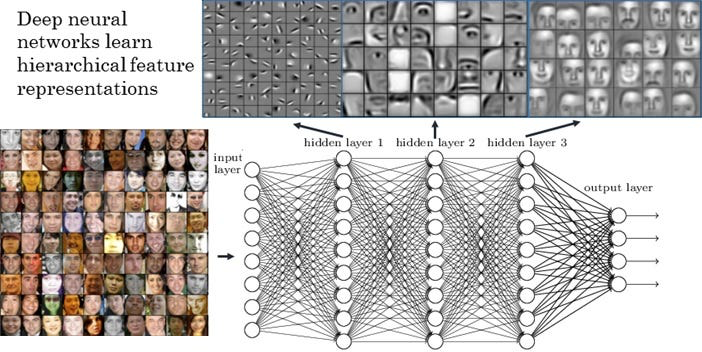
计算图用于logistic回归函数

先回顾一下单一样本的logistic回归损失函数的公式，公式如下：

将logistic函数用计算图表示出来(以两个基础量为例)，计算图如下：

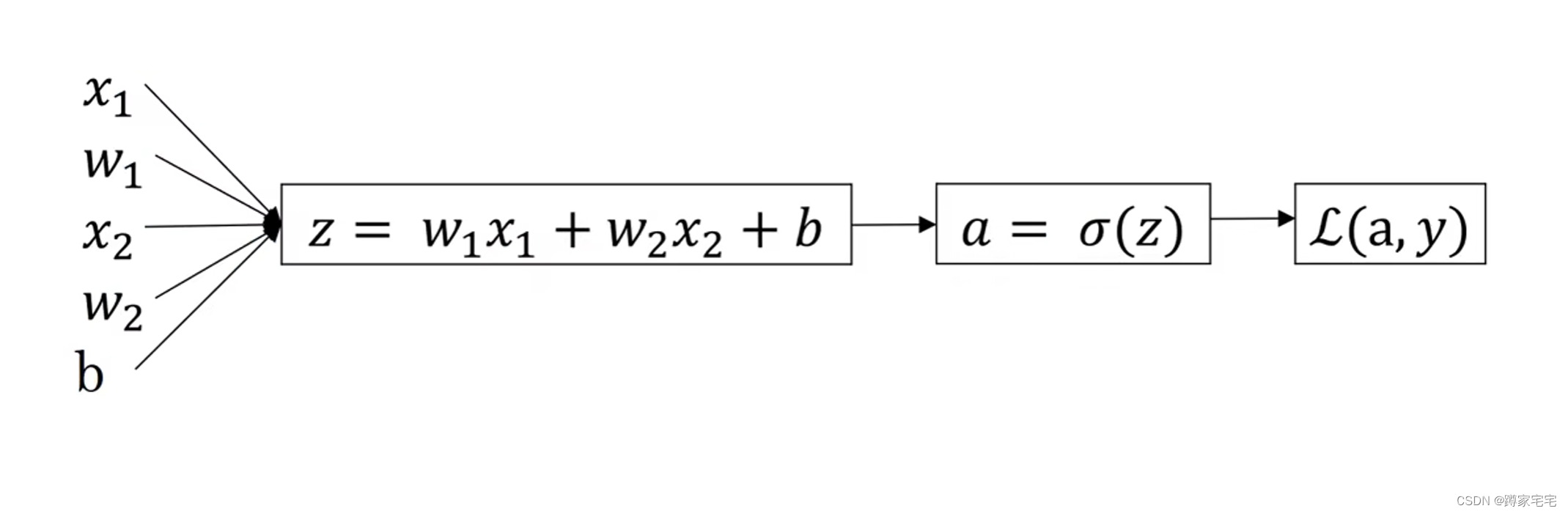
前向传播已经完成，接下来完成后向传播

运用链式法则依次求出 , ,,,

补充梯度下降法--更新变量

当把每个变量的导数求出后，就可以使用梯度下降法进行变量更新

梯度下降法公式：,其中  为学习速率(learning rate)

每次更新迭代计算

m个样本的梯度下降

少量样本的logistic计算图求完后，可以推广到m个样本的计算图

成本函数公式：

每个导数求和之后求平均值(除以m)

代码实现

使用for循环来对m个样本进行后向传播计算

同时在for循环内部嵌套for循环来对i个基础量进行求和

在外层for循环结束后进行基础量的迭代

这样完成简单的迭代算法代码实现

不足之处

两个for循环在大量的样本数据面前，会使迭代时间大大增加，算法效率及其低下

向量化的出现能够很好地解决这个问题