软件测试面试之——前后端问题判定
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/224108.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Python的基本数据类型和数据类型的转换
TOC
数据类型
类型查看 type 可以使用type内置函数查看变量所指的对象类型 a1
b1.0
c"1"
d1,
e[1]
f{1:1}
g{1}print(type(a))
print(type(b))
print(type(c))
print(type(d))
print(type(e))
print(type(f))
print(type(g))isinstance **如字面意思,isinstance()…
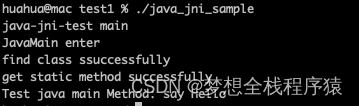
linux运行可执行文件,通过c语言调用java的main方法
前言:以前一直在做Android开发,在某本书上看过一句话“Android上面不只有App类的程序可以运行,能在linux下运行的程序,也可以在Android上面运行” 一.编写C语言部分代码
1.定义java.h头文件
#include <jni.h>#ifndef _JAV…
【微服务】springboot整合kafka-stream使用详解
目录 一、前言
二、kafka stream概述
2.1 什么是kafka stream
2.2 为什么需要kafka stream
2.2.1 对接成本低
2.2.2 节省资源
2.2.3 使用简单
2.3 kafka stream特点
2.4 kafka stream中的一些概念
2.5 Kafka Stream应用场景
三、环境准备
3.1 搭建zk
3.1.1 自定义d…
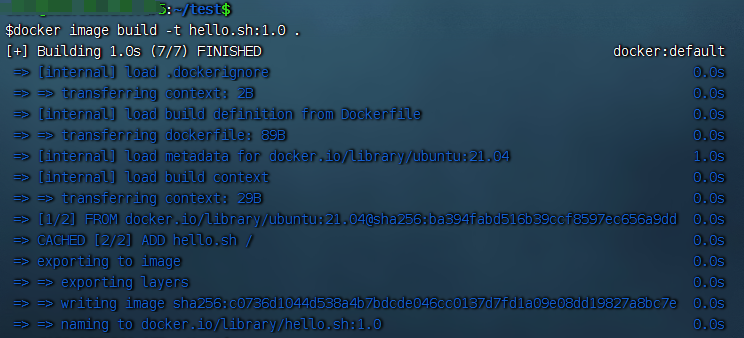
制作自己的 Docker 容器
软件开发最大的麻烦事之一,就是环境配置。用户必须保证操作系统的设置,各种库和组件的安装,只有它们都正确,软件才能运行。docker从根本上解决问题,软件安装的时候,把原始环境一模一样地复制过来。 以 koa-…
RHCE9学习指南 第9章 权限管理
9.1 所有者所属组
为了了解所有者和所属组的概念,我们先看图9-1。 图9-1 用房子来帮助理解所有者和所属组 张老板是公司老板,买了一套房作为员工宿舍给A部门的员工居住。张老板是房主,所以他对房子具有很多权限,A部门员工只能具…
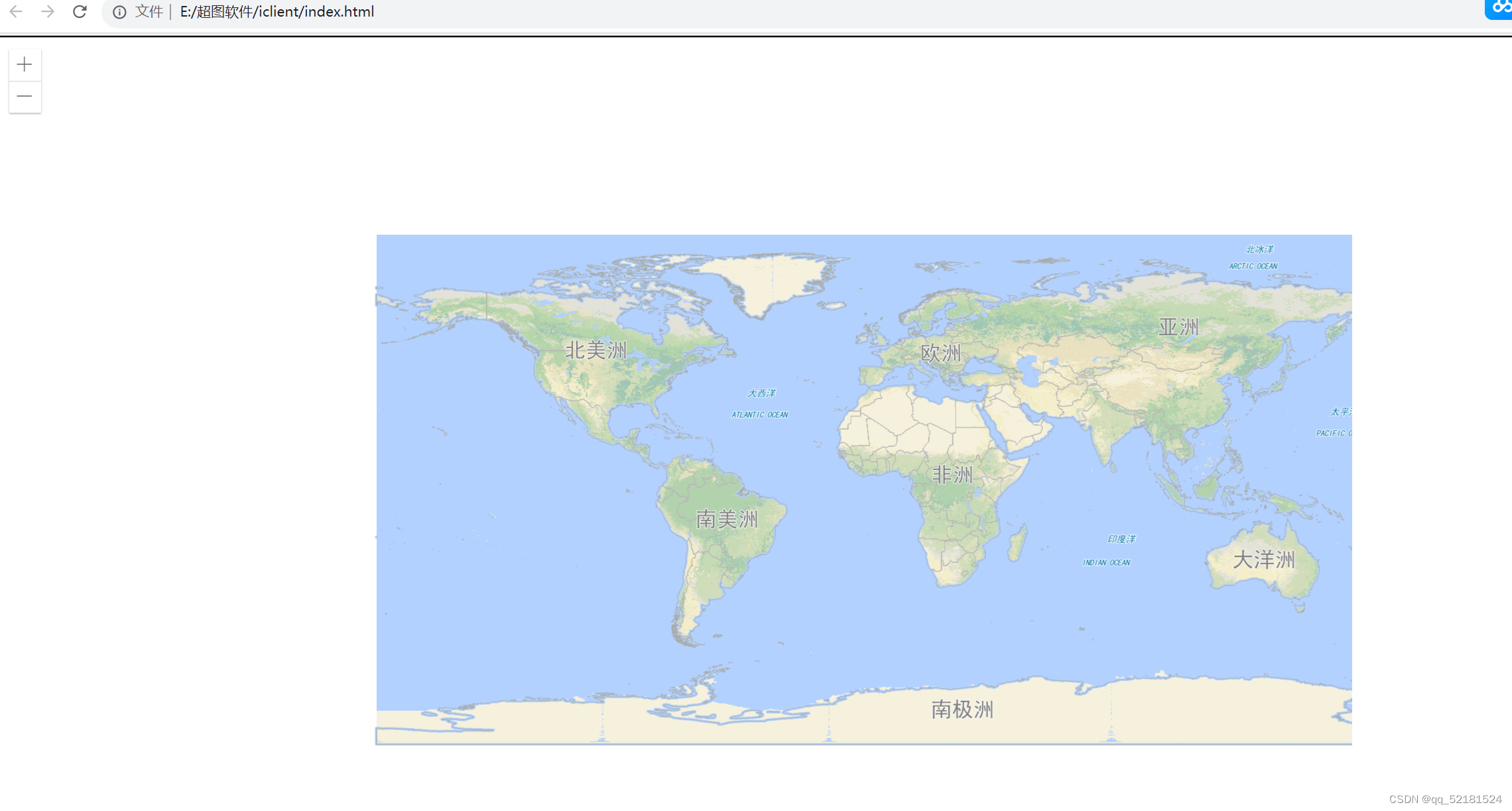
SuperMap iServer发布的ArcGIS REST 地图服务如何通过ArcGIS API加载
作者:yx 文章目录 一、发布服务二、代码加载三、结果展示 一、发布服务
SuperMap iServer支持将地图发布为ArcGIS REST地图服务,您可以在发布服务时直接勾选ArcGIS REST地图服务,如下图所示: 也可以在已发布的地图服务中&#x…
【量化金融】证券投资学
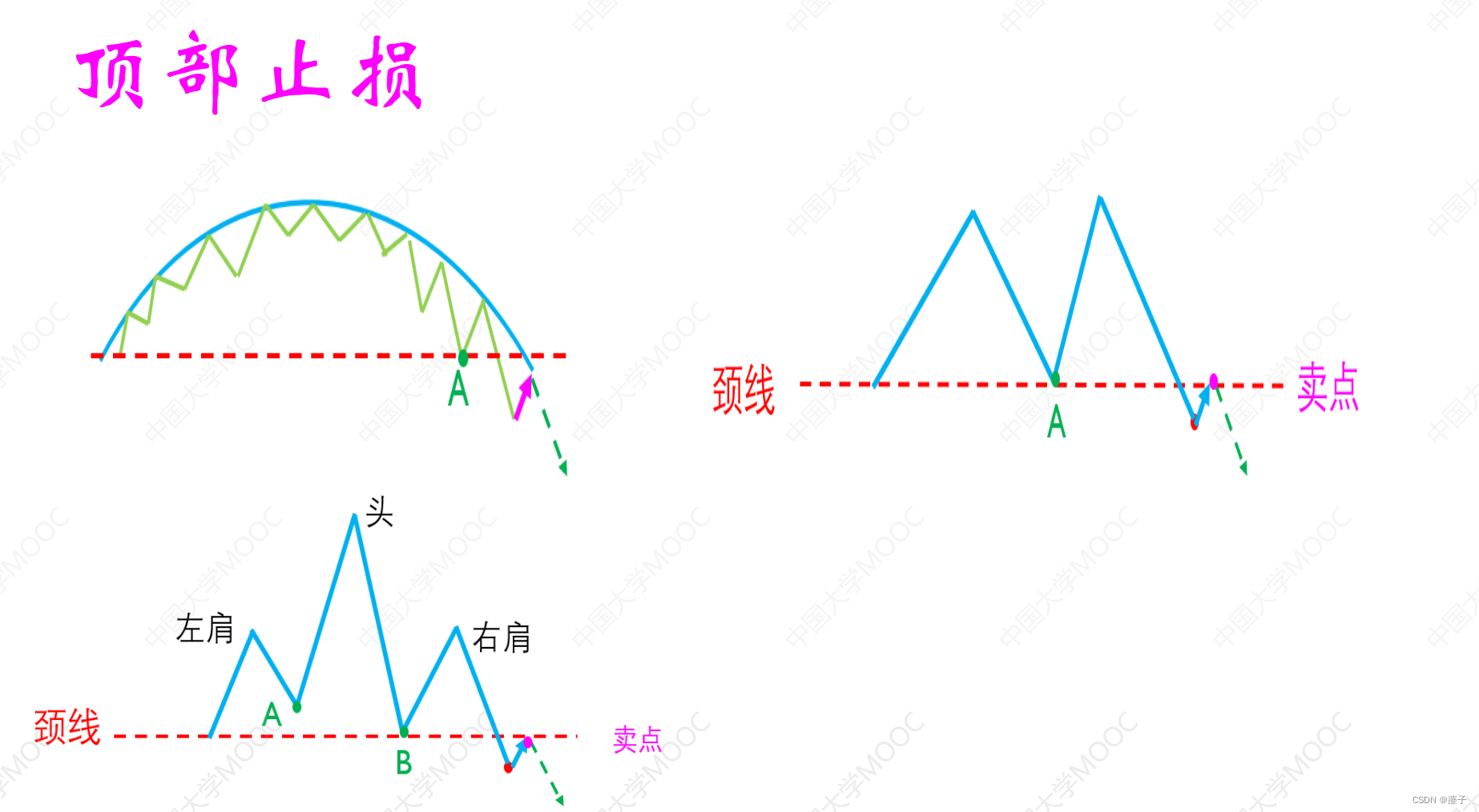
韭菜的自我修养 第一章: 基本框架和概念1.1 大盘底部形成的技术条件1.2 牛市与熊市1.3 交易系统1.3.1 树懒型交易系统1.3.2 止损止损的4个技术 第二章:证券家族4兄弟2.1 债券(1)债券,是伟大的创新(2&#x…
赛宁综合安全验证评估,筑牢关基网络安全屏障
在国际复杂态势和数字经济发展的驱动下,关键信息基础设施(以下简称:关基)的安全运营逐步走向实战化、体系化和常态化。验证评估作为安全运营的试金石,已成为实现动态防御、主动防御的有力手段。如何通过体系化验证评估…
Flutter 三: Dart
1 数据类型 数字(number) int double 字符串转换成 num int.parse(“1”) double.parse(“1”);double 四舍五入保留两位小数 toStringAsFixed(2) 返回值为stringdouble 直接舍弃小数点后几位的数据 可使用字符串截取的方式 字符串(string) 单引号 双引号 三引号三引号 可以输…
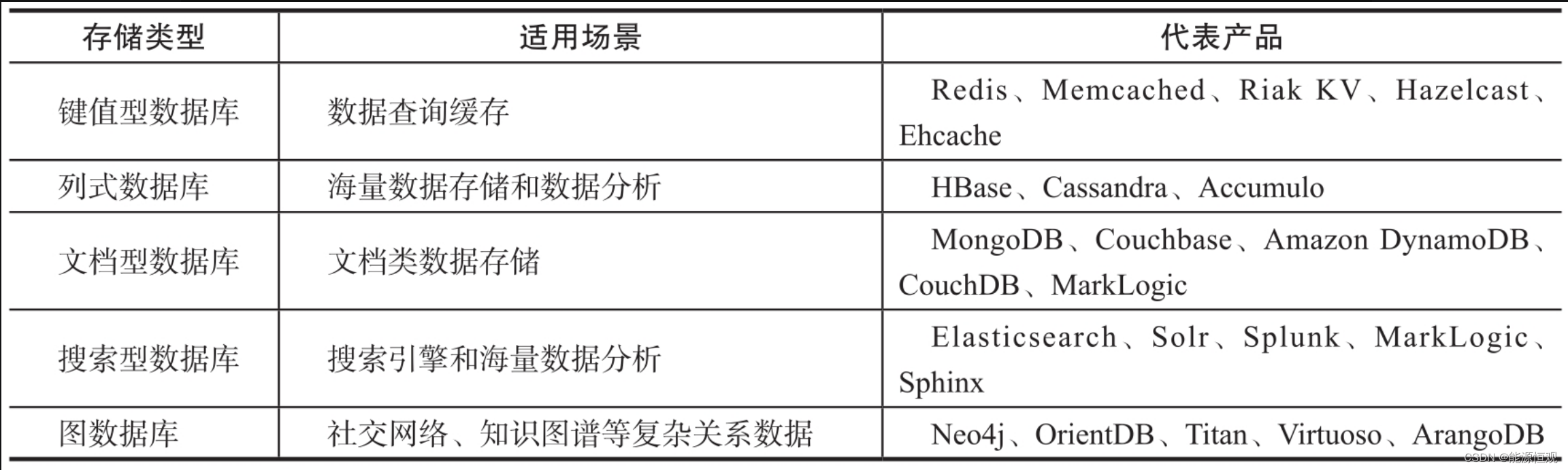
云计算与大数据之间的羁绊(期末不挂科版):云计算 | 大数据 | Hadoop | HDFS | MapReduce | Hive | Spark
文章目录 前言:一、云计算1.1 云计算的基本思想1.2 云计算概述——什么是云计算?1.3 云计算的基本特征1.4 云计算的部署模式1.5 云服务1.6 云计算的关键技术——虚拟化技术1.6.1 虚拟化的好处1.6.2 虚拟化技术的应用——12306使用阿里云避免了高峰期的崩…
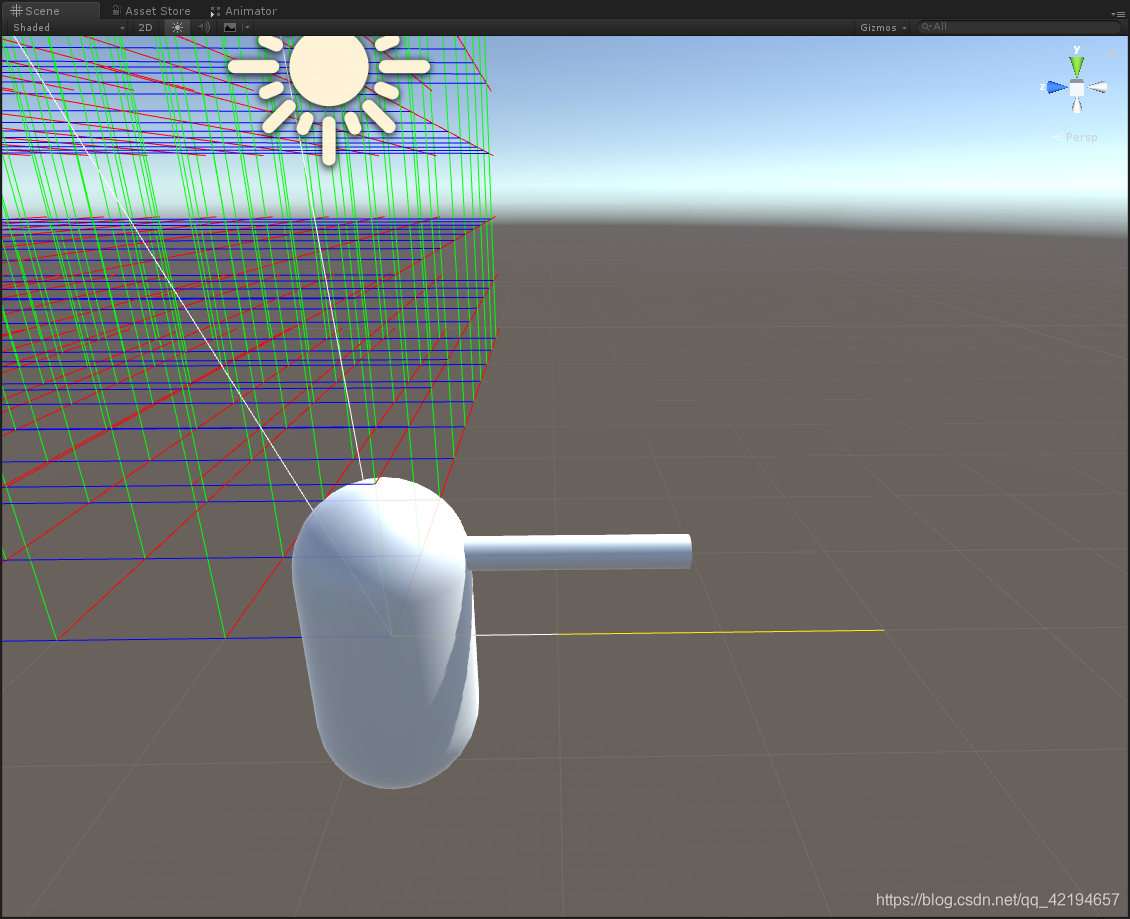
Unity 人物方向旋转详细讲解
Unity 人物方向旋转详细讲解 人物的旋转有很多种一、在介绍之前我们需要理解Unity的向量也就是Vector3二、下面我们创建两个小球f1,f2左边的为f2 右边的为f1 三、我们将小球坐标用白色直线画出来,两个小球之间用黑色线画出来,两个小球的向量用黄线表示接…
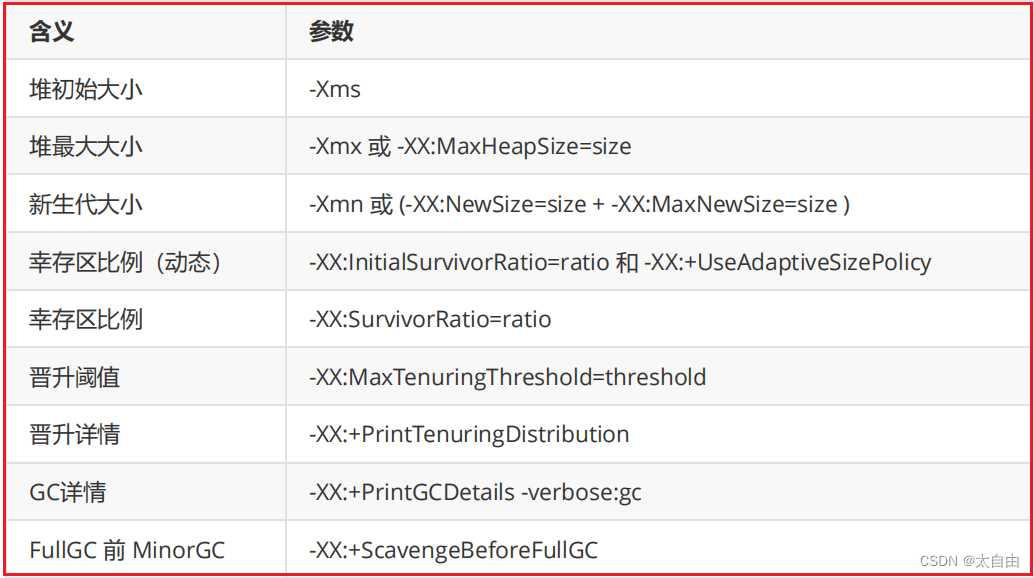
关于JVM的垃圾回收GC的一些记录
目录
一、JVM内存区域划分 二、从一个基本问题开始引入垃圾回收
三、GC作用的区域
三、如何确定一个对象是否可以被当成垃圾进行回收
(1)引用计数法
(2)可达性分析算法
(3)引用的类型
(3…
(Matlab)基于CNN-LSTM的多维时序回归预测(卷积神经网络-长短期记忆网络)
目录
一、程序及算法内容介绍:
基本内容:
亮点与优势:
二、代码实际运行结果展示:
三、部分代码展示:
四、本文完整代码数据下载: 一、程序及算法内容介绍:
基本内容: 本代码…
【Kubernetes】控制器Statefulset
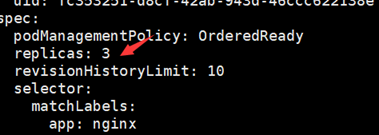
Statefulset控制器 一、概念二、Statefulset资源清单文件编写技巧2.1、查看定义Statefulset资源需要的字段2.2、查看statefulset.spec字段如何定义2.3、查看statefulset的spec.template字段如何定义 三、Statefulset使用案例:部署web站点3.1、编写一个Statefulset资…
【四】记一次关于架构设计从0到1的讨论
记一次关于架构设计从0到1的讨论
简介: 在一次面试中和面试官讨论起来架构设计这个话题,一聊就不知不觉一个小时了,感觉意犹未尽。现在回想起来感觉挺有意思的,古人说独学而无友则孤陋而寡闻,的确是这样的,…
【并发编程篇】读锁readLock()和写锁writeLock()
文章目录 🛸情景引入⭐解决问题 readLock()和writeLock()都是ReadWriteLock接口中定义的方法,用于获取读锁和写锁。 readLock()方法返回一个读锁,允许多个线程同时获取该锁,以进行并发读取操作。如果当前已有一个写锁或其他线程正…
HDFS NFS Gateway(环境配置,超级详细!!)
🐮博主syst1m 带你 acquire knowledge! ✨博客首页——syst1m的博客💘 😘《CTF专栏》超级详细的解析,宝宝级教学让你从蹒跚学步到健步如飞🙈 😎《大数据专栏》大数据从0到秃头👽&…
云原生之深入解析基于FunctionGraph在Serverless领域的FinOps的探索和实践
一、背景
Serverless 精确到毫秒级的按用付费模式使得用户不再需要为资源的空闲时间付费。然而,对于给定的某个应用函数,由于影响其计费成本的因素并不唯一,使得用户对函数运行期间的总计费进行精确的事先估计变成了一项困难的工作。以传统云…
免费福利马上截止!深圳的户外小伙伴别错过!COSP2024体育展来了
COSP2024户外博览会
展会时间:2024年3月14-16日
展会地址:深圳福田会展中心
户外运动爱好者不可错过!
COSP2024户外博览会不仅可以逛展
看各种露营装备、户外器材
还有各种沙龙、峰会活动
就在明年开年,阳春三月天…
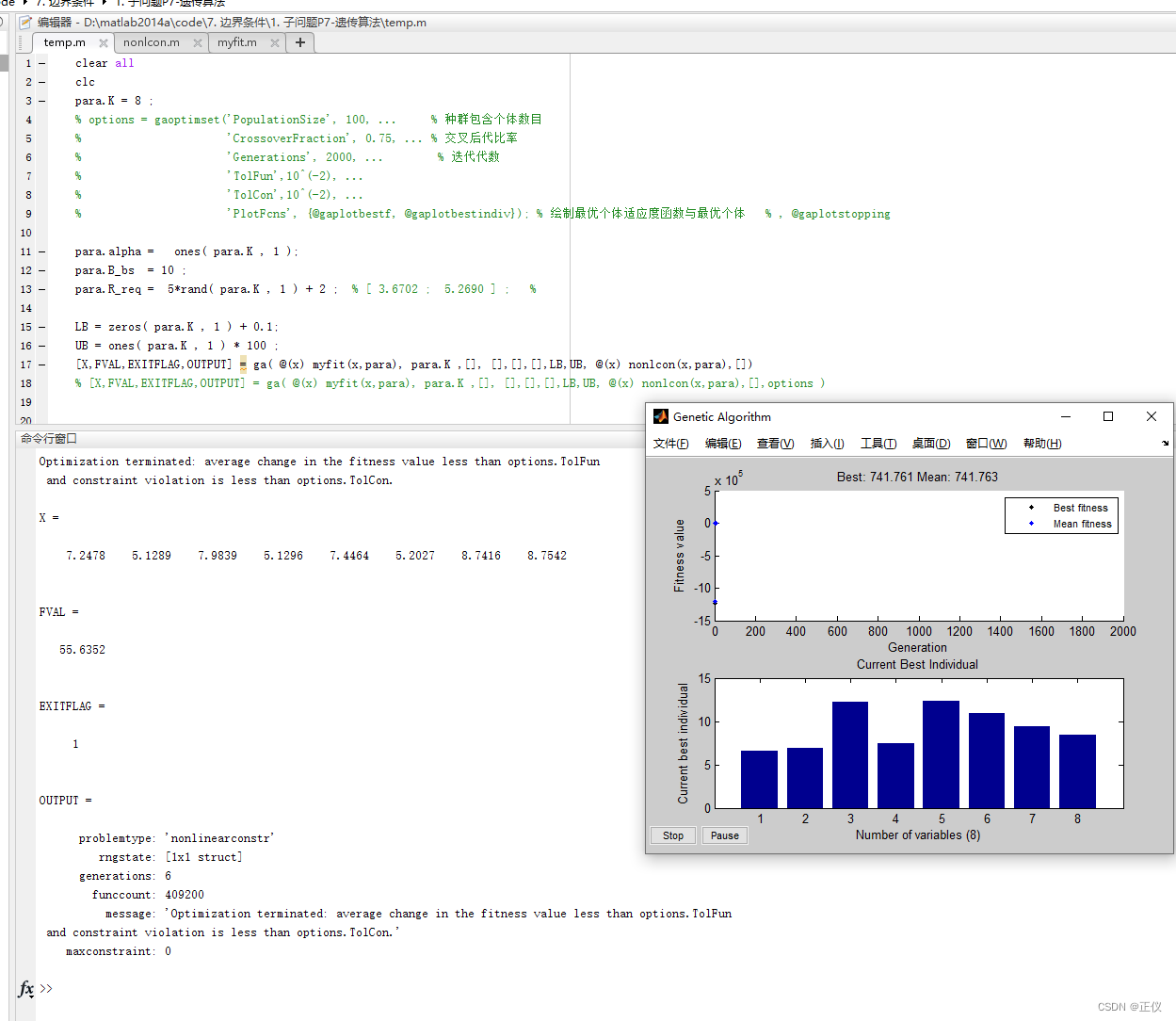
解决 MATLAB 遗传算法中 exitflg=4 的问题
一、优化问题简介
以求解下述优化问题为例: P 1 : min p ∑ k 1 K p k s . t . { ∑ k 1 K R k r e q l o g ( 1 α k ∗ p k ) ≤ B b s , ∀ k ∈ K p k ≥ 0 , ∀ k ∈ K \begin{align} {P_1:}&\mathop{\min}_{\bm{p}}{ \sum\limits_{k1}^K p_k } \no…
推荐文章
- 过去时代的诗与人 : 李太白
- @Cacheable 注解
- LeetCode解法汇总2337. 移动片段得到字符串
- LeetCode解法汇总2476. 二叉搜索树最近节点查询
- 多系统萎缩患者的锻炼秘籍:科学运动,守护健康
- #渗透测试#SRC漏洞挖掘# 操作系统-windows系统bat病毒
- (c语言+数据结构链表)项目:贪吃蛇
- (done) 什么是正定矩阵?Positive Definite Matrices
- (WWW2023)论文阅读-Detecting Social Media Manipulation in Low-ResourceLanguages
- (大集合)AI工具和用法汇总—集合的集合
- (动手学习深度学习)第13章 计算机视觉---图像增广与微调
- (力扣记录)199.二叉树的右视图