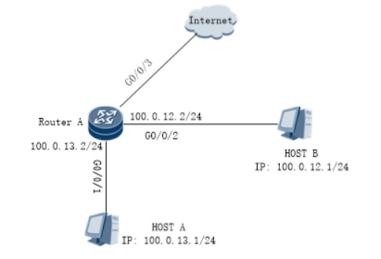
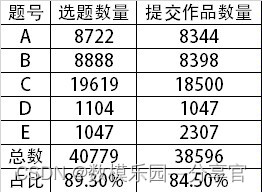
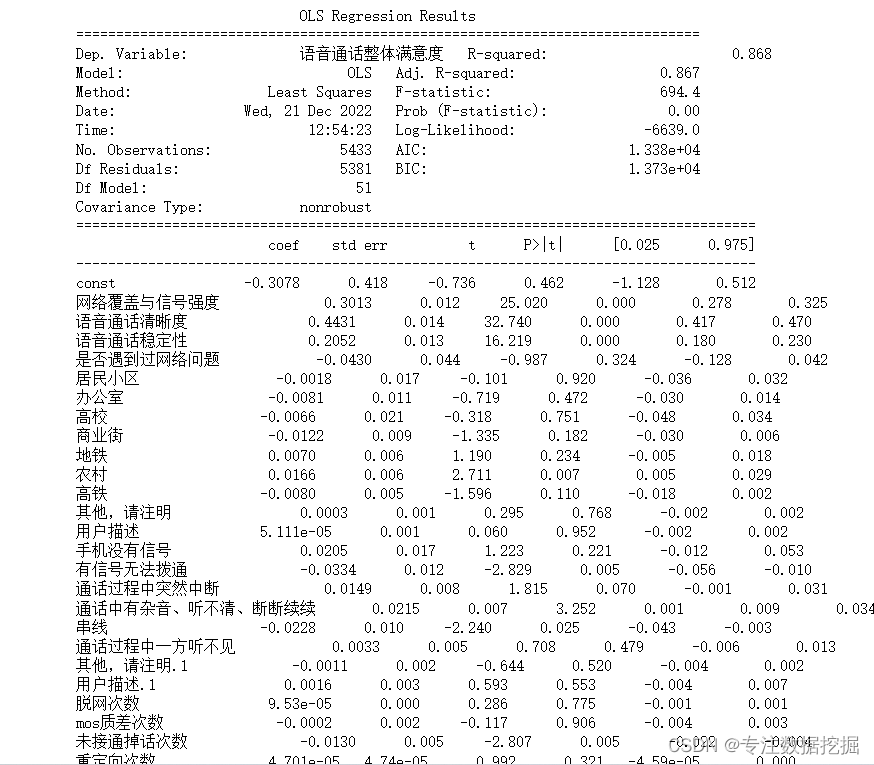
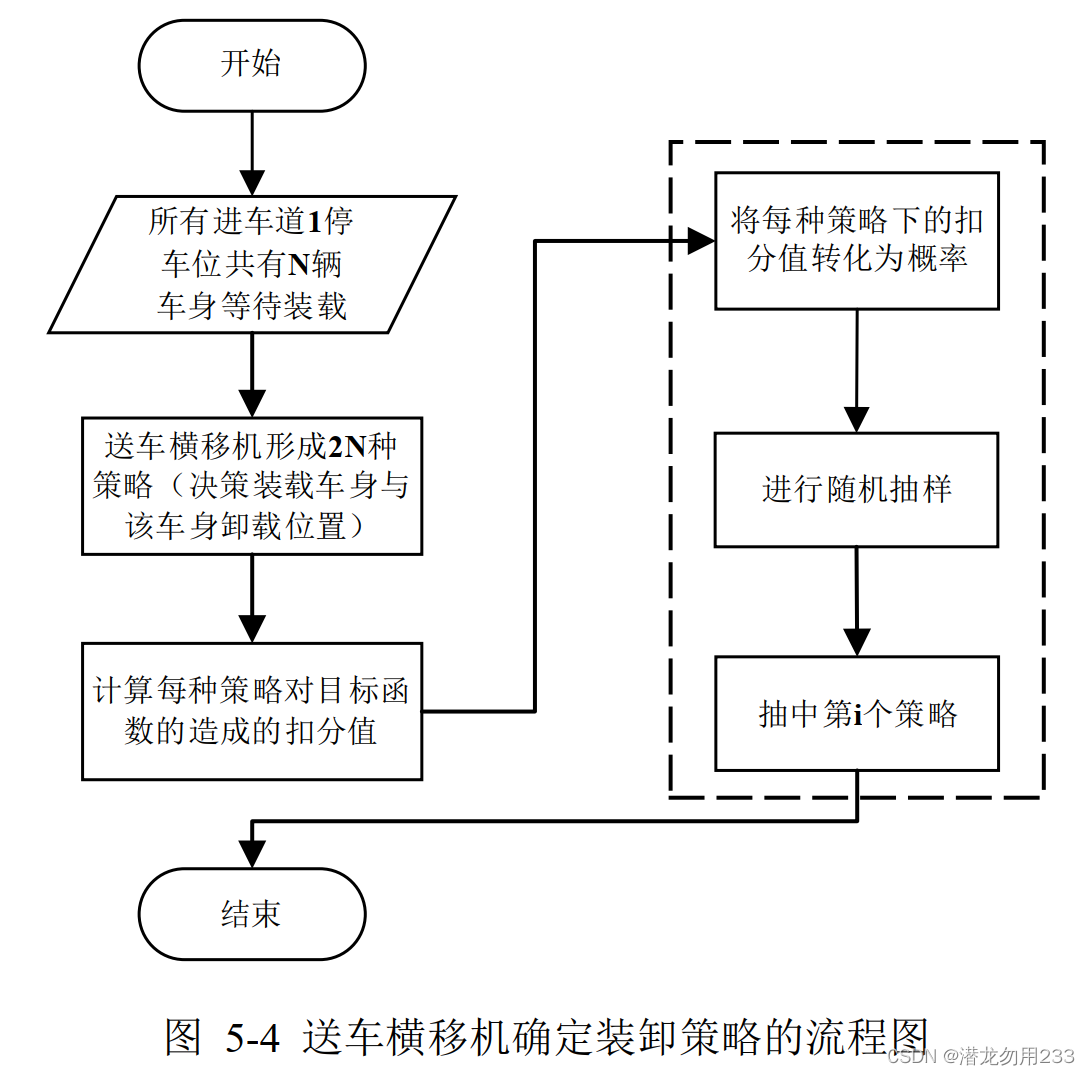
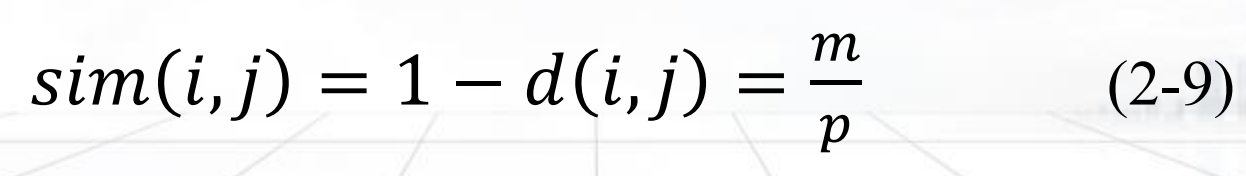这次的题目根据身边同学反映普遍较难,仔细看了一下题目其实也并不难,因为都没有涉及比较复杂的算法,但是这次的题目都比较繁琐,写起来比较费时间。
题目一
题目描述:
已知有一堆人排成M行N列,(M,N均大于等于10小于等于1000),现在从这群人中挑选一些人出来。在这个M行N列的队伍中,每个人对应一个坐标,从最左上角的(0,0)到右下角的(M-1,N-1)。这些人还会进行一次报数,报数顺序是按照类似蜗牛壳形状的顺时针方向由外圈像内圈报数,当报数的个位数为7且十位数为奇数的人出列,按报数顺序输出这些人的坐标。
例如:如下图所示一个5行5列的队伍,按顺时针顺序从外到里报数,其中17满足条件,因此需要输出17的坐标(1,1)

输入和输出格式:
输入为行数M和列数N
10 10
输出为满足条件的坐标:
[[7,9],[1,1],[8,2],[7,5],[4,4]]
要注意输出时候有个坑,前面几组输出坐标后还会输出一个逗号分隔,最后一组坐标之后不输出逗号,因此需要把最后一个满足条件的坐标找出来,输出得时候不输出逗号。
第一题思路
思路比较清晰,就是先创建一个M行N列纯0的数组,然后按照这个顺时针的顺序走一遍下来,并给每个坐标位置赋值(值为这个位置报数号)。然后把满足出列条件的报数的坐标输出即可。按照顺序走的时候需要按照以下的顺序来走:
- 如果该坐标的左边和上边位置已经报过数,且右边位置还未报数,则该位置报数之后向右继续报数。
- 如果该坐标的右边和上边位置已经报过数,且下边位置还未报数,则该位置报数之后向下继续报数。
- 如果该坐标的右边和下边位置已经报过数,且左边位置还未报数,则该位置报数之后向下继续报数。
- 如果该坐标的左边和下边位置已经报过数,且上边位置还未报数,则该位置报数之后向上继续报数。
上面报数的意思其实就是给二维数组赋值的过程,需要注意的是首先要先把最外圈的报数完,因为在进行判断的时候会查询这些坐标相邻外圈元素的状态,如果不先把最外圈的报数,在后面访问时数组会越界。
第一题代码
#include<iostream>
using namespace std;
int main()
{int M,N;cin >> M >> N;int sum0=M*N;//从后往前找找最后一个满足条件的计数。while(sum0>0){int r1 = sum0 % 100;int x1 = r1 % 10;r1 = r1 / 10;int x2 = r1;if(x1==7&&x2%2==1)break;sum0--;//sum0此时为最后一个满足条件的计数}int a[M][N];for (int i0 = 0; i0 < M; i0++)for (int j0 = 0; j0 < N; j0++)a[i0][j0] = 0;int count = 1;int i = 0, j = 0;cout << '[';while (a[i][j] == 0){a[i][j] = count;count++;int s0 = a[i][j];int r0=s0%100;//除以100的余数为后两位数,用r0记录。int y1 = r0 % 10;//y1为个位数r0 = r0 / 10;int y2 = r0;//y2为十位数if(y1==7&&y2%2==1)//满足条件的计数进行输出{cout << '[' << i << ',' << j << ']';if(a[i][j]!=sum0)//最后一个复合条件的报数输出的时候单独处理,不带逗号。cout << ',';}if (i == 0 && j < N - 1)//先把最外圈的进行报数j++;else if (i == 0 && j == N - 1)i++;else if (i < M - 1 && j == N - 1)i++;else if (i == M - 1 && j == N - 1)j--;else if (i == M - 1 && j > 0)j--;else if (i == M - 1 && j == 0)i--;else if (i > 1 && j == 0)i-- ;else if (i == 1 && j == 0)j++;//开始内圈报数;else if (a[i - 1][j]>0 && a[i][j - 1]>0 && a[i][j + 1] == 0)j++;else if (a[i - 1][j]>0 && a[i][j + 1]>0 && a[i + 1][j] == 0)i++;else if (a[i + 1][j]>0 && a[i][j + 1]>0 && a[i][j - 1] == 0)j--;else if (a[i +1][j]>0 && a[i][j - 1]>0 && a[i - 1][j] == 0)i--;}cout << ']';return 0;
}
运行结果:

调试过程中记录队伍报数编号的矩阵:

题目二
题目描述
给定二叉树每个节点的深度,计算多少种满足条件的二叉树。根节点深度为0.
输入描述:
第一行为一个整数N,表示二叉树节点的数量,在1到1000之间。
第二行为N个整数,d1,d2,……dN表示每个节点的深度。
输出描述:
输出为满足条件的二叉树数量。由于结果可能非常大,因此输出为实际结果除以(10^9+7)之后的余数。
例:
输入:
4
1 0 2 2
输出:
2
例子解读:
上面的输入表示深度为1的节点有一个,深度为0的节点有一个,深度为2的节点有两个。对应的两种二叉树的形状如下图所示:由答案为2可以知道该题目不区分元素的不同,只根据二叉树的形状进行分类。如果考虑元素分布的话,下图中D2-1和D2-2交换位置则又多了一倍的种类,因此此题目只考虑多少种形状的二叉树即可,即只考虑组合不考虑排列。

第二题思路
该题如果高中排列组合学的比较好的话应该比较容易想到思路,理清了数学关系这道题目就很简单了。
首先要根据输入把二叉树每层多少个节点数目统计好。例如D0,D1,D2……DN分别表示第0层,1层,……N层的节点数目。对于第i层,该层有Di个节点,则第i+1层有2Di个位置,因此需要从2Di个位置中选D(i+1)个位置进行放置,则放置方法有
种。然后把所有层的放置方法数全部乘起来就得到最后总的不同形状二叉树数量。
如上面的例子:第0 1 2层的节点数为1 1 2.因此对于第一层,有2个位置选一个有2种选取方法,对于第2层,从2个位置选两个有1种选择方法,因此总方法有2*1=2种方法,也就是两种不同形状的二叉树。
第二题代码
#include<iostream>
#include<math.h>
using namespace std;int zuhe(int m, int n)//定义计算组合数的函数//组合数计算公式:m个里面选n个,结果为m!/((m-n)!n!)=(m*(m-1)*...(m-n+1))/(n*(n-1)*...1);//使用(m*(m-1)*...(m-n+1))/(n*(n-1)*...1)计算比m!/((m-n)!n!)能节省较多的运算量。{int m0 = 1, n0 = 1;//m0,n0表示组合数计算中的分子和分母。for (int i = 0; i < n;i++){m0 = m0 * (m - i);n0 = n0 * (n - i);}return m0 / n0;}
int main()
{int N;cin >> N;int di;int a[N] = {0};//用a[N]来记录每层的节点个数,初始化为0,后面每输入一个在对应的层数加1.int depth = 0;//depth记录二叉树深度(层数),N个节点的二叉树深度小于N,for (int i = 0; i < N;i++){cin >> di;a[di]++;if(di>depth)depth = di;}long long count = 1;//记录总方法数,为二叉树各层组合数的乘积。结果可能比较大,使用longlong类型。int cmn;for (int i = 1; i <= depth;i++){cmn = zuhe(2 * a[i - 1], a[i]);//调用组合函数计算每层有多少种组合方法。count = count * cmn;}int r0 = pow(10, 9) + 7;//pow默认返回值为double,这里转为int类型方便下面求余运算。int ans=count%r0;cout << ans;return 0;
}
运行结果:


题目三
题目描述
俄罗斯方块,输入有两个字符串,第一个frame表示当前底座状态,第二个brick表示下落方块的状态,下落的方块只能左右移动不会旋转。方块落下后如果一行全部充满则会消失,最后求最少还剩多少行。输入的底座和方块都不超过9列,即最大只有9列。
例如:
输入为:
2122
121
底座和方块状态如下图所示:其中2122表示当前底座状态,都是底对齐的,而121表示下落方块的状态,都是顶对齐的,即2的位置的突出是往下凸而不是往上凸。下图运行结果为1,下图中方块左右移动有两种下落方式,一种如下图所示,下落后会消去两行最后剩余1行。另外一种下落方式是向又移动一格然后再下落,最后消去一行剩余3行,因此最少的结果是剩余1行,输出为1
输出为:
1

第三题思路
该题思路非常简单,把方块从左到右依次落下并记录剩余的行数,取行数最小的输出。但写起来较为繁琐,关键是如何表示方块。可以用一个二维数组来表示。如上面的例子,共有两种下落方法,一种是靠左边,此时将各列相加可得到3332.
| 1 | 2 | 1 | |
|---|---|---|---|
| 2 | 1 | 2 | 2 |
| 3 | 3 | 3 | 2 |
注意方块下落所在的三列,高度都为3,和方块的顶对齐保持一致。说明这些列下方没有空格。如下图所示:

而靠右边下落的情况,将各列相加得2243。
| 1 | 2 | 1 | |
|---|---|---|---|
| 2 | 1 | 2 | 2 |
| 2 | 2 | 4 | 3 |
注意方块下落所在的三列高度分别为243,不满足方块的顶部对齐条件。因此除了高度最高的那列之外,剩下的俩列都有空格,高度为2的有两个空格,高度为3的有一个空格。如下图所示:在处理中需要特别注意。另外输入的是字符串,需要把每个单独转化为数字处理。

第三题代码
#include<iostream>
#include<string>
using namespace std;
int main()
{string frame;string brick;cin >> frame>>brick;//输入底座和掉落的方块。int framelen = frame.size();//求底座列数int bricklen = brick.size();//求方块列数int leftmin = 10000;//表示剩余最小行数,初始为一个较大的数。int frame0[framelen], brick0[bricklen];//将输入的字符串转为数字保存到整型数组中。for (int i = 0; i < framelen;i++)frame0[i] = frame[i] - '0';//因为列数小于9,减去0的ascii值即可将字符串转为响应的数字。for (int i = 0; i < bricklen;i++)brick0[i] = brick[i] - '0';int num = framelen - bricklen + 1;//左右移动方块共有num种掉落方法。for (int i = 0; i < num;i++){int frameadd[framelen];for (int j = 0; j < framelen;j++)frameadd[j] = frame0[j];int height = 0;for (int j = i; j < i + bricklen; j++){frameadd[j] = frameadd[j] + brick0[j-i];if(frameadd[j]>height)height = frameadd[j];//height记录方块所在列的最高高度。}int framefin[framelen][height];//使用二维数组framefin记录方块下落后的状态。for (int j1 = 0; j1 < framelen;j1++)for (int j2 = 0; j2 < height;j2++)framefin[j1][j2] = 0;//先初始为全0;for (int j1 = 0; j1 < framelen;j1++)for (int j2 = 0; j2 < frame0[j1];j2++)framefin[j1][j2] = 1;//先把下落前的底座用1填充。for (int j1 = i; j1 < i + bricklen;j1++){ int num0 = height - frameadd[j1];//num0记录砖块和基座之间的空格数目。for (int j2 = frame0[j1] + num0; j2 < height;j2++)framefin[j1][j2] = 1;//跳过空格然后再填充1,空格数为最高的高度减去当前列高度。}//下面进行判断消去的多少行,每消去一行height-1,最后剩余的行数为height。int height0 = height;for (int j2 = 0; j2 < height0;j2++)//这个地方单独定义一个height0控制循环次数,因为height在循环体内会改变,如果还要用height,循环次数会变化。{int flag = 1;//如果j1行不全为1,则改变flag的值。for (int j1 = 0; j1 < framelen;j1++){if(framefin[j1][j2]==0){flag = 0;break;}}if(flag==1)//如果flag未改变,则表明这一行全为1,则消去一行height--;}if(height<leftmin)leftmin = height;//legtmin记录最小行数。}cout << leftmin;return 0;
}
}
运行结果: