本文参考辽宁石油化工大学于晶贤教授的演示文档聚类分析之系统聚类法及其SPSS实现。
目录
1.样品与样品间的距离
2.指标和指标间的“距离”
相关系数
夹角余弦
3.类与类间的距离
(1)类间距离
(2)类间距离定义方式
1.最短距离法
2.最长距离法
3.组间平均连接法
4.组内平均连接法
5.重心法
4.常用系统聚类法
系统聚类法过程
5.例子
最短距离系统聚类法
1.写出样品间的距离矩阵(以欧氏距离为例)
2.将每一个样品看做是一个类
3.观察 D(G2,G4)= 15.9最小
4.观察 D(G6,G7)= 18.2最小
5.最后将G8与G3聚为一类,记为G9
6.该聚类的谱系图
最长距离系统聚类法
1.写出样品间的距离矩阵(以欧氏距离为例)
2.将每一个样品看做是一个类
3.观察 D(G2,G4)= 15.9最小
4.观察 D(G63,G7)= 32.4最小
5.最后将G8与G6聚为一类,记为G9
6.该聚类的谱系图
其它系统聚类法
聚类分析需要注意的问题
系统聚类法的Spss实现
1.录入数据
2.选择方法
3.统计量和绘制选项
4.方法和保存选项
总结
1.样品与样品间的距离
各种距离如下:
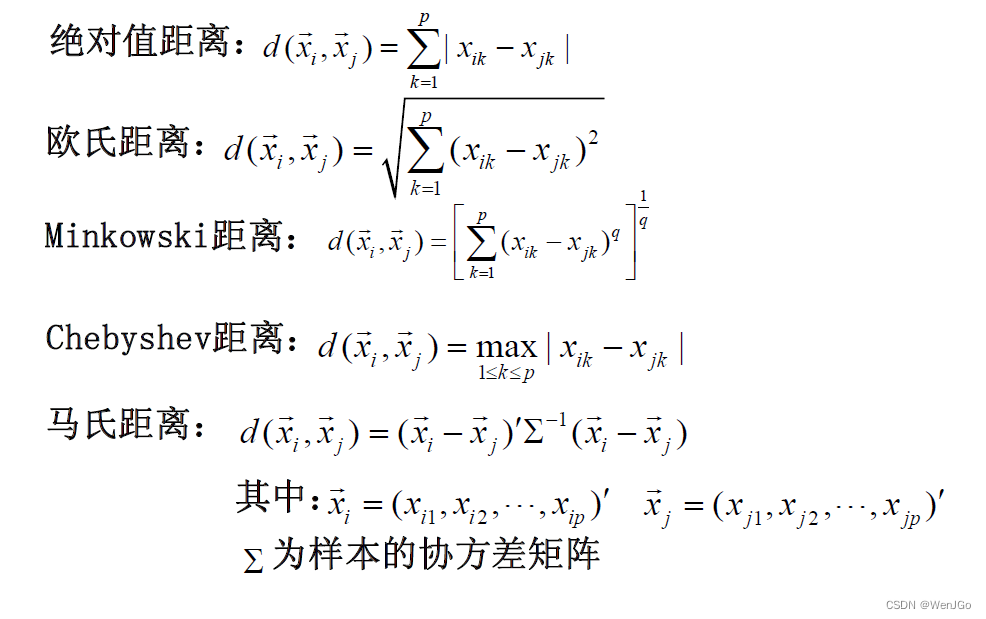
最常用的还是绝对值距离(特定距离),和欧式距离
举例使用如下

2.指标和指标间的“距离”
相关系数

夹角余弦

举例如下

3.类与类间的距离
(1)类间距离
由一个样品组成的类是最基本的类,如果每一类都由一个样品组成,那么样品间的距离就是类间距离。
(2)类间距离定义方式
如果某一类包含不止一个样品,那么就要确定类间距离,类间距离是基于样品间距离定义的,大致有如下几种定义方式:
1.最短距离法
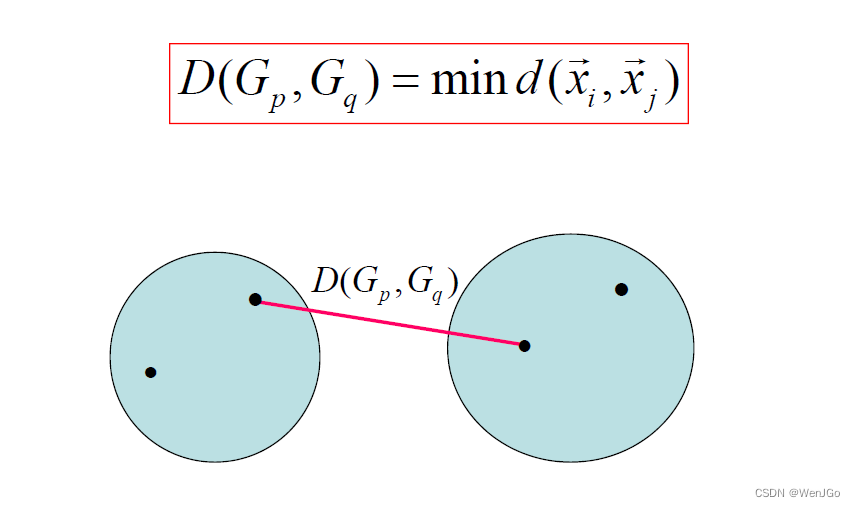
2.最长距离法

3.组间平均连接法

4.组内平均连接法

5.重心法

4.常用系统聚类法
系统聚类法过程

5.例子
最短距离系统聚类法

1.写出样品间的距离矩阵(以欧氏距离为例)

2.将每一个样品看做是一个类
G1,G2,G3,G4,G5,观察D(G1,G5) = 15.8最小,故将G1与G5聚为一类,记为G6。
计算新类与其余各类之间的距离,得到新的距离矩阵D1


3.观察 D(G2,G4)= 15.9最小
故将G2与G4聚为一类,记为G7.
计算新类与其余各类之间的距离,得到新的距离矩阵D2


4.观察 D(G6,G7)= 18.2最小
故将G6与G7聚为一类,记为G8.
计算新类与其余各类之间的距离,得到新的距离矩阵D3

5.最后将G8与G3聚为一类,记为G9
6.该聚类的谱系图

最长距离系统聚类法
1.写出样品间的距离矩阵(以欧氏距离为例)

2.将每一个样品看做是一个类
即G1,G2,G3,G4,G5,观察D(G1,G5) = 15.8最小,故将G1与G5聚为一类,记为G6。
计算新类与其余各类之间的距离,得到新的距离矩阵D1


3.观察 D(G2,G4)= 15.9最小
故将G2与G4聚为一类,记为G7.
计算新类与其余各类之间的距离,得到新的距离矩阵D2


4.观察 D(G63,G7)= 32.4最小
故将G3与G7聚为一类,记为G8.
计算新类与其余各类之间的距离,得到新的距离矩阵D3

5.最后将G8与G6聚为一类,记为G9
6.该聚类的谱系图

其它系统聚类法
(1)组间平均连接系统聚类法
(2)重心系统聚类法
(3)组内平均连接系统聚类法
注:这些方法的差别就是在计算新类与其余各类间的距离,
如需学习详细内容,可参考多元统计分析相关书籍。参考教材:《多元统计分析》,何晓群,中国人民大学出版社,2008.
《多元统计分析》,于秀林,中国统计出版社,2006.
聚类分析需要注意的问题
(1)对于一个实际问题要根据分类的目的来选取指标,指标选取的不同分类结果一般也不同。
(2)样品间距离定义方式的不同,聚类结果一般也不同。
(3)聚类方法的不同,聚类结果一般也不同(尤其是样品特别多的时候)。最好能通过各种方法找出其中的共性。
(4)要注意指标的量纲,量纲差别太大会导致聚类结果不合理。
(5)聚类分析的结果可能不令人满意,因为我们所做的是一个数学的处理,对于结果我们要找到一个合理的解释。
系统聚类法的Spss实现
1.录入数据

2.选择方法

3.统计量和绘制选项

4.方法和保存选项
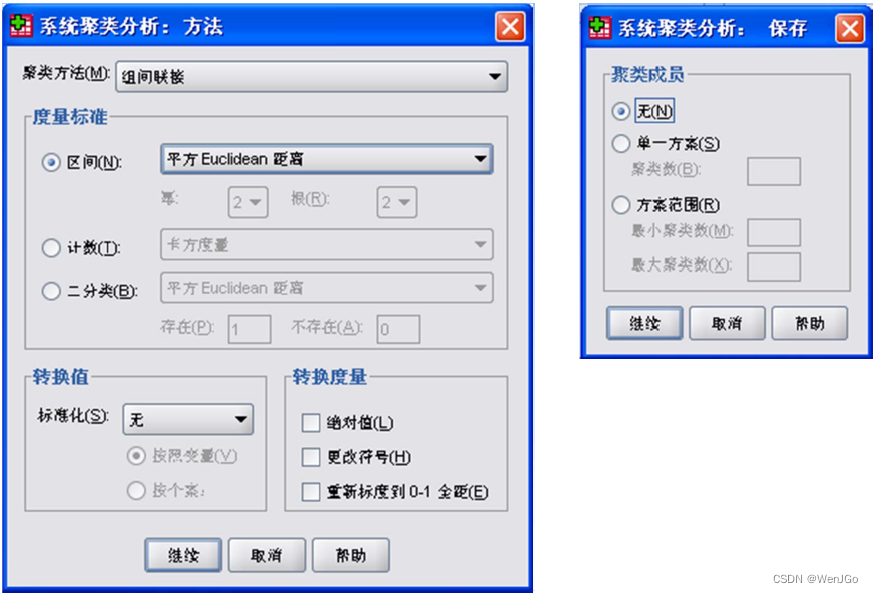
总结
知识点较多,但是一通百通,具体大家可以参考于晶贤老师的具体内容。
ヾ( ̄▽ ̄)Bye~Bye~